第10章 控制系统的状态空间设计
极点配置
1. 引言与基本概念
1.1 极点配置与根轨迹法的区别
极点配置法是状态空间设计法的核心内容之一,它与经典的根轨迹法在设计思路上有显著区别:
1.2 适用前提
进行极点配置设计时,通常基于以下假设:
-
全状态可测:假设所有用于反馈的状态变量都是可以观测(测量)的 。若不可测,则需要引入状态观测器 。
-
状态完全可控:这是能够任意配置极点的核心条件。
-
系统类型:主要讨论单输入单输出(SISO)系统。
2. 状态反馈系统的结构
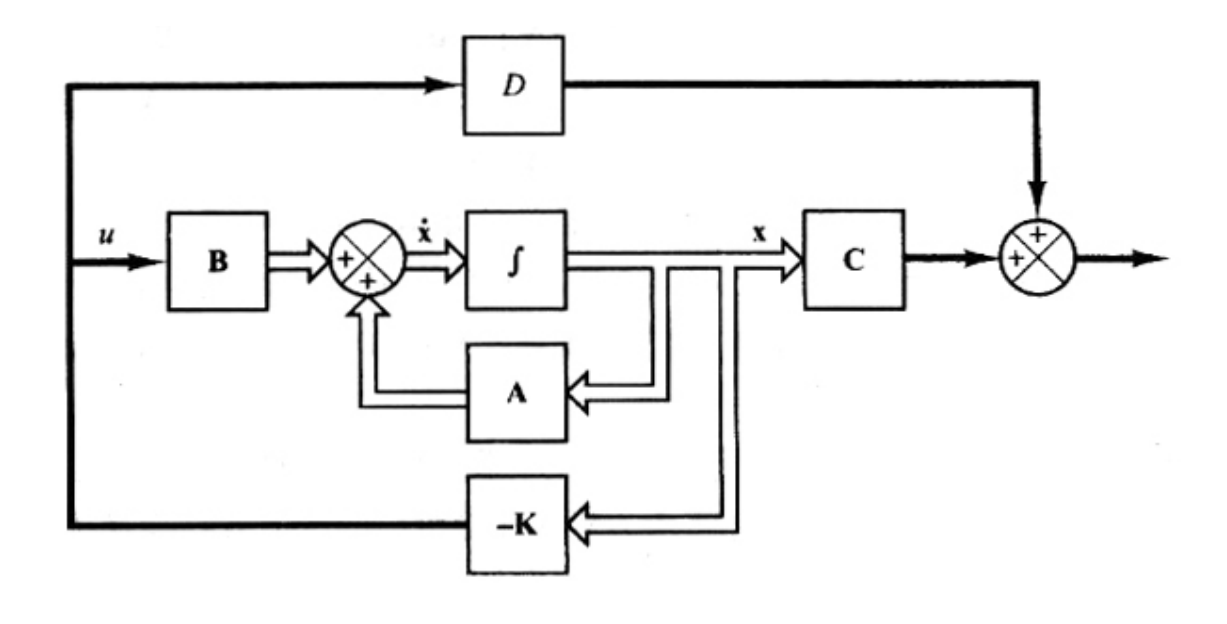
![image-20251218204615918]()
2.1 系统描述
考虑线性定常连续系统:
{x˙=Ax+Buy=Cx+Du
2.2 控制律(状态反馈)
选取线性状态反馈控制律:
u=−Kx
这意味着控制信号由系统的瞬时状态决定。
- K:状态反馈增益矩阵,对于SISO系统,其维数为 1×n 。
2.3 闭环系统方程
将控制律代入原状态方程,得到闭环系统的状态方程:
x˙=Ax+B(−Kx)=(A−BK)x
该方程的解为:
x(t)=e(A−BK)tx(0)
显然该系统的闭环特征方程为
∣sI−(A−BK)∣=0
2.4 调节器极点
-
矩阵 A−BK 的特征值被称为调节器极点。
-
系统的稳态和瞬态响应特性完全由 A−BK 的特征值决定。
-
如果所有调节器极点均位于左半平面,当 t→∞ 时,x(t)→0,系统稳定。
-
极点配置问题:就是通过选择矩阵 K,将调节器极点(闭环极点,A−BK 的特征值)配置到期望位置的问题。
注:
- 该闭环控制系统(调节器系统)无输入量,或者说参考输入恒为0,控制系统的目的是保持输出量为0
- 调节器系统 (Regulator):参考输入始终为零或非零常数,目的是保持输出为零或恒定。
- 控制系统 (Control System):参考输入是时变的。
3. 极点任意配置的充要条件
3.1 定理
系统闭环极点能够进行任意配置的充分必要条件是:系统状态完全可控。
3.2 必要性证明 (如果不完全可控,则不能任意配置)
思路:利用Kalman规范分解证明不可控部分的特征值无法被改变。
- 假设系统不完全可控,则可控性矩阵的秩 rank(M)=q<n 。
- 通过线性变换 x=Px^,将系统按可控性进行分解。选取 P 使得前 q 列线性无关(构成可控子空间),后 n−q 列为附加的补余向量。
P=[f1f2⋯fqvq+1vq+2⋯vn]
- 变换后的系统矩阵 A^ 和输入矩阵 B^ 具有如下形式:
A^=P−1AP=[A110A12A22],B^=P−1B=[B110]
-
定义变换后的反馈增益 K^=KP=[k1k2] 。
-
闭环特征多项式为:
∣sI−(A−BK)∣=∣sI−(A^−B^K^)∣=sI−[A110A12A22]+[B110][k1k2]=[sIq−A11+B11k10−A12+B11k2sIn−q−A22]=∣sIq−A11+B11k1∣⋅∣sIn−q−A22∣
- 结论:∣sIn−q−A22∣ 部分的特征值(A22 的特征值)完全取决于原系统,与反馈增益 K 无关。因此,若系统不完全可控,不可控部分的特征值无法配置。
- 即为了任意配置矩阵 A−BK 特征值,系统必须是状态完全可控的。
3.3 充分性证明 (如果完全可控,则可任意配置)
思路:将系统变换为可控标准形,证明反馈可以影响特征方程的所有系数。
-
若系统完全可控,存在变换矩阵 T,使得 x^=T−1x 变换后的系统为可控标准形。
-
可控标准形矩阵 A^ 的最后一行包含原特征方程的系数 −an,…,−a1 。
-
输入矩阵 B^=[0,…,0,1]T 。
x^˙=A^x^+B^u=T−1ATx^+T−1Bu
其中
A^=T−1AT=00⋮0−an10⋮0−an−101⋮0−an−2……⋱……00⋮1−a1,B^=T−1B=00⋮01
- 在可控标准形下,施加反馈 u=−K^x^,其中 K^=KT=[δnδn−1⋯δ1] 。
- 闭环系统矩阵 A^−B^K^ 相比状态矩阵 A^ 仅在最后一行发生变化,原系数 −ai 变为 −(ai+δi) 。
A^−B^K^=T−1AT−T−1BKT=00⋮0−an10⋮0−an−101⋮0−an−2……⋱……00⋮1−a1−00⋮01[δnδn−1⋯δ1]=00⋮0−(an+δn)10⋮0−(an−1+δn−1)01⋮0−(an−2+δn−2)……⋱……00⋮1−(a1+δ1)
闭环特征多项式变为
∣sI−(A^−B^K^)∣=∣sI−(T−1AT−T−1BKT)∣=s0⋮0an+δn1s⋮0an−1+δn−101⋮0an−2+δn−2……⋱……00⋮1s+a1+δ1=sn+(a1+δ1)sn−1+⋯+(an−1+δn−1)s+(an+δn)
- 新的特征方程为:
sn+(a1+δ1)sn−1+⋯+(an−1+δn−1)s+(an+δn)=0
- 设期望的特征方程为:
sn+α1sn−1+⋯+αn−1s+αn=0
- 通过比较同幂次系数(使同幂次系数相等),可得 αi=ai+δi,从而解出唯一的 δi(即 K^),再反变换回原坐标系 K=K^T−1。因此,只要可控,即可任意配置。
4. 极点配置的设计步骤与算法
方法一:变换矩阵法 (适用于高阶系统)
利用可控标准形变换矩阵 T 来求解 K。
步骤:
-
检验可控性条件:计算可控性矩阵 M=[B,AB,…,An−1B] 并检验其秩是否为 n 。
-
求开环特征多项式系数:计算 ∣sI−A∣=sn+a1sn−1+⋯+an,确定 a1,…,an 的值。
-
构造变换矩阵 T:
T=MW
其中 M 为可控性矩阵
M=[BAB⋯An−1B]
W 为托普利兹矩阵(Toeplitz-like matrix):本质上是可控标准型的可控性矩阵的逆矩阵,考试时需记忆该形式并直接代入开环多项式系数数值
W=an−1an−2⋮a11an−2an−3⋮10……⋱……a11⋮0010⋮00
- 写出期望特征多项式:根据期望极点 μi,展开得到 ∏i=0n(s−μi)=sn+α1sn−1+⋯+αn
- 计算反馈增益矩阵 K:
K=[αn−an∣αn−1−an−1∣…∣α1−a1]T−1
注意:系数向量元素的顺序对应从常数项系数差到 sn−1 系数差
方法二:直接代入法 (适用于 n≤3 的低阶系统)
直接利用特征方程系数相等求解。
步骤:
- 设 K=[k1,k2,…,kn] 。
- 计算闭环特征多项式(特征方程)符号表达式 ∣sI−A+BK∣ 。
- 计算期望特征多项式(特征方程) (s−μ1)…(s−μn)=sn+α1sn−1+⋯+αn 。
- 令两式中 s 的同次幂系数相等,建立方程组解出 ki
∣sI−A+BK∣=(s−μ1)…(s−μn)⟹k1,k2,⋯,k3
5. 期望极点的选择策略
如何选择闭环极点的位置是设计的关键:
-
主导极点法:基于根轨迹经验,配置一对主导闭环极点以满足阻尼比和自然频率要求,其余极点配置在远离虚轴的左侧(远离主导极点)。
-
折中原则:
- 响应速度 vs 控制能量:需要在可接受的响应速度与控制能量之间权衡。
- 响应速度过快(极点过远左侧)意味着需要大的控制能量,这会导致执行机构笨重且成本增加。
-
最优控制:另一种方法是基于二次型最佳控制(LQR)来确定极点。
6. 设计实例详解
题目:
给定系统 A=00−110−501−6,B=001。要求配置闭环极点为 s=−2±j4 和 s=−10。求 K 。
求解过程:
- 可控性检验:
M=[B,AB,A2B]=00101−61−631
rank(M)=3,系统完全可控。
- 确定原系统参数 (ai):
∣sI−A∣=s3+6s2+5s+1
故 a1=6,a2=5,a3=1。
-
确定期望系统参数 (αi):期望多项式 =(s+2−j4)(s+2+j4)(s+10)=(s2+4s+20)(s+10)=s3+14s2+60s+200。故 α1=14,α2=60,α3=200 。
-
计算 K (方法1:变换矩阵法):
-
由于原系统已经是可控标准形(友矩阵形式),故变换矩阵 T=I 。
-
根据公式 K=[α3−a3,α2−a2,α1−a1]T−1。
-
K=[200−1,60−5,14−6]=[199,55,8] 。
-
计算 K (方法2:直接代入法):
- 计算 ∣sI−A+BK∣:
dets01+k1−1s5+k20−1s+6+k3=s3+(6+k3)s2+(5+k2)s+(1+k1)
- 对比期望多项式 s3+14s2+60s+200。
- 方程组:
⎩⎨⎧6+k3=14⟹k3=85+k2=60⟹k2=551+k1=200⟹k1=199
- 结果:K=[199,55,8] 。
状态观测器 (State Observers)
1. 状态观测器的基本概念
在现代控制理论的状态反馈设计中,通常假设所有的状态变量都是可测量的。但在实际系统中,并非所有状态都能直接通过传感器测量(受限于成本、物理实现等)。
- 定义:用于估计或观测系统内部不可测状态变量的装置称为状态观测器(State Observer)。
- 作用:利用系统可测量的输入量 u 和输出量 y,重构出系统的全部状态向量 x~,用于状态反馈。
- 分类:
- 全阶状态观测器 (Full-order State Observer):观测系统的所有 n 个状态变量,无论其是否可测。
- 降阶/最小阶观测器 (Reduced/Minimum-order Observer):若系统有 m 个输出可测,仅估计剩下的 n−m 个状态变量。
2. 全阶状态观测器的数学模型
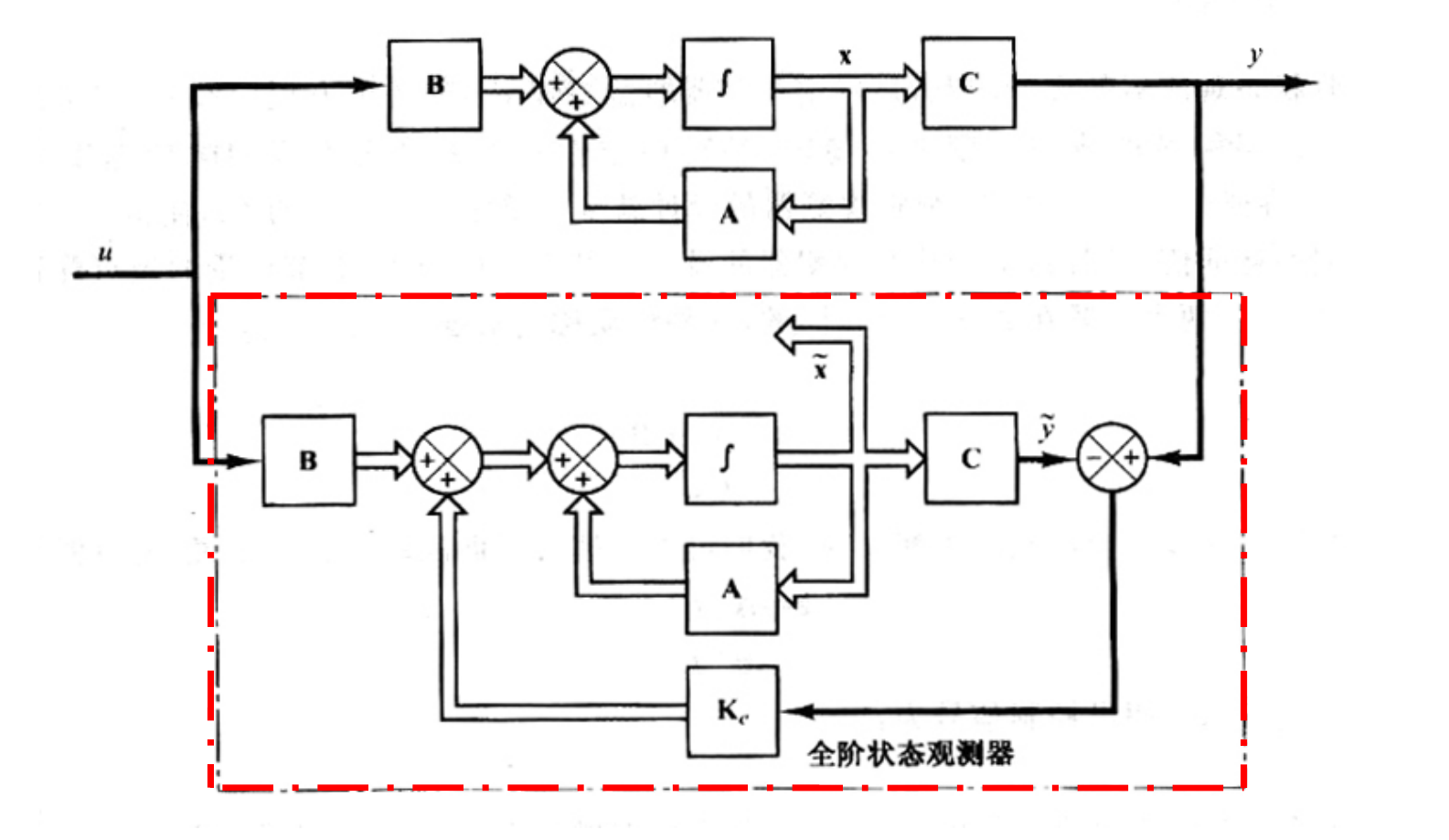
![image-20251229164828076]()
2.1 结构与方程
全阶观测器本质上是原系统的一个数学模型,并在其基础上增加了一个基于输出误差的校正项。
{x˙=Ax+Buy=Cx
x~˙=Ax~+Bu+Ke(y−Cx~)
整理后可得:
x~˙=(A−KeC)x~+Bu+Key
其中
- Ke 为观测器增益矩阵(Observer Gain Matrix)。
- y−Cx~:输出估计误差。该项用于补偿模型参数(A, B)的不精确性以及初始状态估计(初始状态与估计的初始状态之间)的偏差。
2.2 估计误差动态特性 (Error Dynamics)
为了验证观测器的有效性,必须分析估计误差随时间的变化。
e˙=x˙−x~˙=(Ax+Bu)−[Ax~+Bu+Ke(Cx−Cx~)]=A(x−x~)−KeC(x−x~)=(A−KeC)e
- 结论:误差为 $$\dot{e} = (A - K_eC)e$$
- 误差向量 e(t) 的动态特性完全由矩阵 A−KeC 的特征值决定。
- 稳定性要求:如果 A−KeC 是稳定矩阵(即所有特征值具有负实部,特征值落在LHP),则对任意初始误差 e(0),当 t→∞ 时,e(t)→0,即估计值 x~ 收敛于真值 x 。
- 如果系统是完全可观测的,则可证明,可以选择 Ke,使得 A−KeC 具有任意所期望的特征值。
3. 观测器的设计与对偶原理
3.1 观测器设计的本质
- 前提条件:如果系统是完全可观测的,则可证明,可以选择 Ke,使得 A−KeC 具有任意所期望的特征值。
- 设计全阶观测器的问题,转化为确定增益矩阵 Ke,使得 A−KeC 具有期望的特征值(极点)。
3.2 对偶问题 (Dual Problem)
观测器设计问题与状态反馈的极点配置问题在数学上是对偶的。
- 原系统:(A,B,C)
{x˙=Ax+Buy=Cx
- 对偶系统:(A∗,C∗,B∗)
{z˙=A∗z+C∗vn=B∗z
- 关系1:原系统的可观性矩阵(行向量形式)和对偶系统的可控性矩阵相同
Qc′=[C∗A∗C∗⋯]=Qo
- 关系2:原系统的观测器特征多项式与对偶系统的状态反馈特征多项式相同
∣sI−(A∗−C∗K)∣=∣sI−(A−K∗C)∣=∣sI−(A−KeC)∣
其中 Ke=K∗ (即为原系统的观测器增益矩阵)
3.3 设计的充分必要条件
能设计状态观测器(即能任意配置观测器极点)的充要条件是:
-
原系统的对偶系统是状态完全可控的 。
-
等价于:原系统是状态完全可观测的。
3.4 求取 Ke 的方法
变换法 (Ackermann公式的推广)
- 检验对偶系统可控性条件或原系统可观性条件:计算 Qc′=[C∗A∗C∗⋯] 并检验其秩是否为 n
- 求对偶系统的开环矩阵多项式系数:∣sI−A∗∣=sn+a1sn−1+⋯+an,确定 a1,…,an 的值。
- 构造变换矩阵 T: T=Qc′W,其中
W=an−1an−2⋮a11an−2an−3⋮10……⋱……a11⋮0010⋮00
- 写出期望的观测器特征多项式:根据期望的观测器极点 μi,展开得到 ∏i=0n(s−μi)=sn+α1sn−1+⋯+αn
- 计算观测器增益矩阵 Ke:
Ke=K∗=([αn−an∣αn−1−an−1∣…∣α1−a1]T−1)∗=(T−1)∗αn−anαn−1−an−1⋯α1−a1=(WQo)−1αn−anαn−1−an−1⋯α1−a1
推导用到一些矩阵运算性质,我线代学得一坨屎,希望没错:由于W是实对称矩阵,Q_c转置正好是列向量形式Q_o,对于前面乘的变换矩阵可以做如下化简
(T−1)∗=(T∗)−1=(W∗Qc′∗)−1=(WQo)−1
Qo 为原系统的可观性矩阵的列向量形式
注意:系数向量元素的顺序对应从常数项系数差到 sn−1 系数差
直接代入法
Qc′=[C∗A∗C∗⋯]=Qo,rank(Qc′)=n
- 设观测器增益矩阵 Ke=[ke1,ke2,…]T
- 将其代入特征多项式 ∣sI−(A−KeC)∣,并令其等于期望的观测器特征多项式
- 通过对比 s 的同次幂系数求解
∣sI−(A−KeC)∣=(s−μ1)⋯(s−μn)
3.5 最佳 Ke 的选择与折中
-
响应速度:Ke 较大时,估计误差收敛快(响应快)。
-
噪声敏感度:如果测量输出 y 含有噪声,Ke 过大不仅会放大噪声,还可能引入高频干扰。
-
设计原则:Ke 的选择是快速响应与对干扰/噪声灵敏度之间的折中。通常观测器的极点应选得比系统主导极点快,但不能过远以免带宽过大引入噪声。
4. 观测器-状态反馈控制系统 (分离定理)
当系统状态不可测时,使用观测到的状态 x~ 代替真实状态 x 进行反馈。
4.1 系统构成
x˙=Ax−BKx~=Ax+B[−K(x−e)]=(A−BK)x+BKe
结合误差方程 e˙=(A−KeC)e,可得 4.2 中结论
4.2 增广矩阵与特征方程
将状态 x 和误差 e 组合成增广状态向量,得到整个闭环系统的状态空间表达式:
[x˙e˙]=[A−BK0BKA−KeC][xe]
该方程描述了观测-状态反馈控制系统的动态特性
由于系统矩阵是分块上三角矩阵,其特征多项式为对角线上两块特征多项式的乘积,特征方程为:
特征方程=∣sI−(A−BK)∣⋅∣sI−(A−KeC)∣=0
4.3 分离性质 (Separation Principle)
- 重要结论:观测器-状态反馈系统的闭环极点集合,等于由极点配置单独设计的极点与由观测器单独设计的极点的并集。
- 这意味着:极点配置(控制器设计)和观测器设计是相互独立的,可以分步进行,互不影响。
5. 控制器-观测器的传递函数
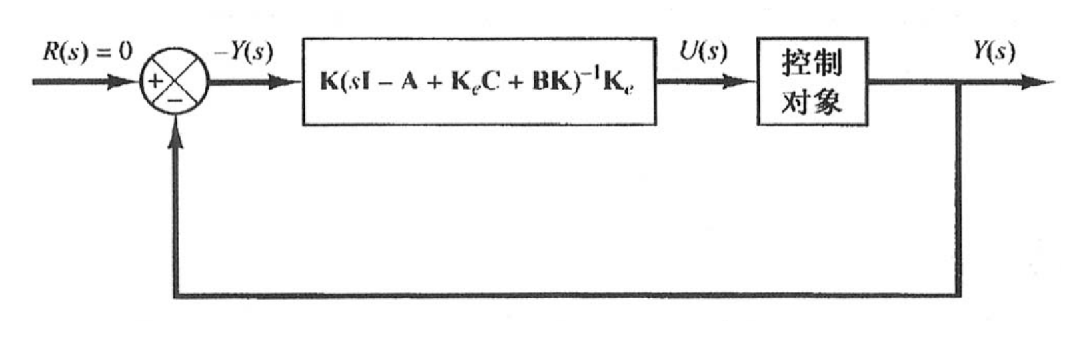
将观测器和反馈增益视为一个整体(动态控制器),可以推导其从输出 y 到输入 u 的传递函数。
Y(s)U(s)=−K(sI−A+KeC+BK)−1Ke
这个传递函数代表了反馈回路中的补偿器部分(总的控制器部分)。
简要推导过程:
采用观测器观测到的状态作为状态反馈
u~=−Kx~⟹x~˙=(A−KeC)x~+Bu+Key=(A−KeC−BK)x~+Key
进行 Laplace 变换
X~(s)=(sI−A+KeC+BK)−1KeY(s)
最后代入状态反馈方程的Laplace变换
u~=−Kx~⟶LU(s)=−KX~(s)=−K(sI−A+KeC+BK)−1KeY(s)
整理一下可得从输入到输出的传递函数 Y(s)U(s)
![image-20251229174255693]()
![image-20251218110447525]()
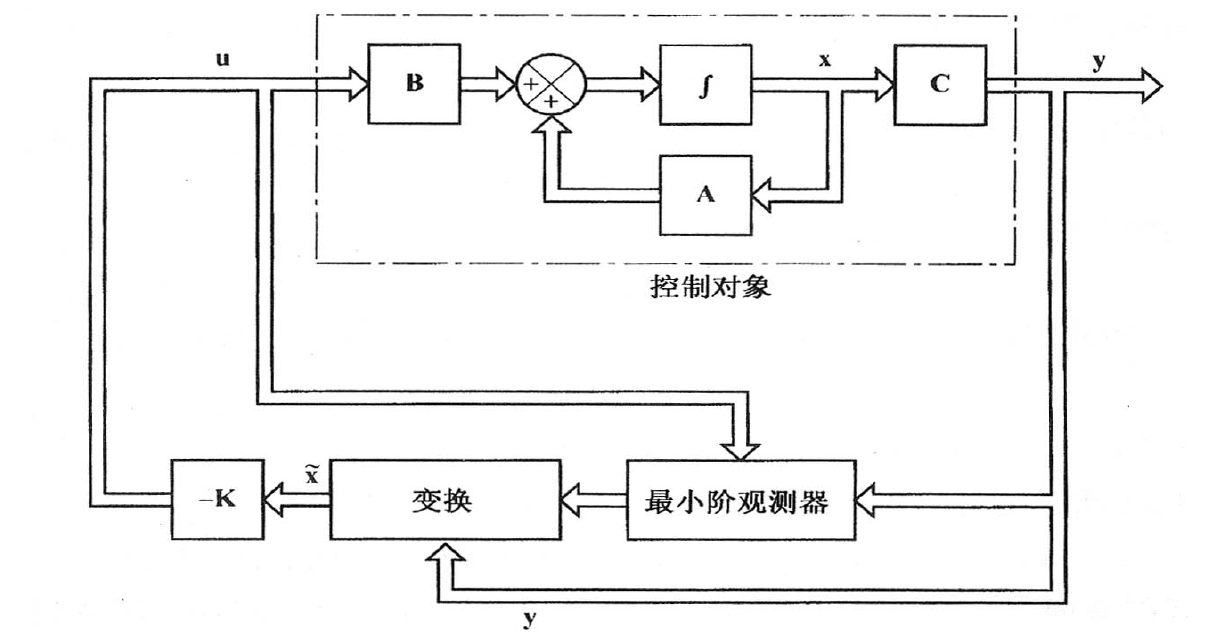
6. 最小阶观测器 (Minimum-Order Observer)
- 原理:若输出向量 y 是可测量的 m 维向量,且这 m 个输出变量是状态的线性组合,则这 m 个状态变量是已知的。
- 需观测器观测的阶数:观测器只需要估计剩余的 n−m 个状态变量。
- 特点:最小阶观测器的阶数为 n−m,通常比全阶观测器计算量小,结构更简单。
![image-20251229175431638]()
7. 带观测器的调节器系统设计流程
7.1 设计步骤
- 建模:推导系统的状态空间模型。
- 极点选择:
- 选择期望的闭环控制极点(决定系统性能)。
- 选择期望的观测器极点(通常应比控制极点快,且需位于左半平面)。
- 计算增益:确定状态反馈增益矩阵 K 和观测器增益矩阵 Ke。
- 仿真与校验:检验对给定初始条件的响应。如果不满意(如超调过大或噪声敏感),需调整极点位置重算。
7.2 参考输入系统的结构
对于有参考输入 r 的系统,观测器控制器的介入位置有多种结构(如参考输入加在观测器回路外或内),需确保输出 y 能跟随输入 r 。
8. 总结与注意事项
-
时域方法的优势:基于极点配置与观测器的状态空间法功能强大,适用于多变量系统。
-
稳定性裕量 (Stability Margins):引入观测器通常会降低系统的稳定裕量。设计完成后,建议使用频率响应法(如伯德图)检查稳定裕量。
-
噪声与带宽:观测器极点选得过远(带宽过大)会导致高频噪声通过。这是一个工程折中问题。
-
经典与现代结合:虽然状态空间法很强,但如果能用低阶校正装置(经典控制方法)解决,应优先采用经典方法。