第二章 控制系统的数学模型
2.1 引言与基本概念
1. 控制系统
一个完整的控制系统由若干个元件相互配合构成。系统的正常工作取决于各个物理量之间相互作用与相互制约的关系。信号的传递体现为能量的传递(如放大、转化、储存),系统最终会由动态过程达到平衡状态(稳定运动)。
2. 数学模型
- 定义:描述系统变量间相互关系的动态性能的运动方程。
- 重要特性:一个系统的数学模型不唯一。
3. 建立数学模型的方法
- 解析法:依据系统及元件所遵循的物理或化学规律(如牛顿定理、欧姆定理、热平衡定律等)列写出数学关系式,从而建立模型。
- 实验法(系统辨识):人为地对系统施加某种测试信号,记录其输出响应,并用适当的数学模型进行逼近。
4. 数学模型的形式
-
时域 (Time Domain)
-
微分方程 (Differential Equation):描述连续系统。
a0y(n)+a1y(n−1)+⋯+any=b0x(m)+b1x(m−1)+⋯+bmx(n≥m)
-
差分方程 (Difference Equation):描述离散系统。
-
状态空间方程 (State-Space Equations):现代控制理论常用。
{x˙(t)=A(t)x(t)+B(t)u(t)y(t)=C(t)x(t)+D(t)u(t)
-
复频域 (Complex Frequency Domain)
-
传递函数 (Transfer Function):经典控制理论核心
G(s)=a0sn+a1sn−1+⋯+anb0sm+b1sm−1+⋯+bm
-
方框图 (Block Diagram):系统的图形化表示。
-
频域 (Frequency Domain)
- 频率响应/正弦传递函数 (Sinusoidal Transfer Function):G(jω)
5. 线性系统及其分类
- 线性系统 (Linear System):满足叠加原理的系统。
- 线性定常系统 (Linear Time-Invariant, LTI):由线性定常集总参数元件构成的动态系统,可用常系数线性微分方程描述。
- 线性时变系统 (Linear Time-Varying, LTV):描述系统的微分方程的系数是时间的函数。
6. 建立数学模型的步骤
- 划分环节:按功能将系统划分为不同的组成部分(元件或环节)。
- 写出运动方程式:为每个环节写出描述其输入输出关系的运动方程。
- 消去中间变量:通过代数运算消去内部变量。
- 写成标准形式:将最终的方程整理成标准形式,通常是将与输出量有关的项放在方程左边,输入量有关的项放在右边,并按导数降幂排列。
2.2 传递函数和脉冲响应函数
1. 传递函数 (Transfer Function)
-
定义:对于线性定常系统,在全部初始条件为零的假设下,系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。
G(s)=L[输入量]L[输出量]初始条件为零=X(s)Y(s)=a0sn+a1sn−1+⋯+anb0sm+b1sm−1+⋯+bm(n≥m)
-
系统阶次:传递函数分母多项式的最高阶次 n 称为系统的阶次。
-
性质:
- 传递函数的概念的适用范围限于线性常微分方程系统
- 传递函数是复数
s 的代数方程,它只取决于系统自身的结构和参数,与输入信号的形式无关。
- 传递函数和系统的微分方程可以相互转换。
- 不同的物理系统可能具有相同的传递函数。
- 传递函数一旦被确定,就能够对系统的动态特性进行充分地描述。
2. 特征方程、零点和极点
G(s)=N(s)M(s)=a0sn+a1sn−1+⋯+anb0sm+b1sm−1+⋯+bm(n≥m)
-
特征方程 (Characteristic Equation):传递函数分母多项式 N(s)=0 称为特征方程
- 它决定着系统的动态特性。
- N(s) 的最高阶次
-
特征根 (Characteristic Roots):特征方程的根。
-
零点 (Zeros):传递函数分子多项式 M(s)=0 的根。
-
极点 (Poles):传递函数分母多项式 N(s)=0 的根。系统的极点就是系统的特征根。
-
零、极点分布图:在复平面上表示出系统所有零点(用 “○” 表示)和极点(用 “×” 表示)的图形。
-
闭环零点、闭环极点:闭环系统的零点、极点。大部分研究的闭环系统没有零点。画闭环极点的时候会加个方框
3. 静态增益 (Static Gain)
-
定义:当 s=0 时传递函数的值,记为 K。(称为系统的放大系数或静态增益或稳态增益)
K=G(0)=anbm
-
物理意义:当系统处于静态(稳态)时,输出量与输入量的比值。
-
为什么 G(0) 是系统的静态增益?
-
稳态增益(Steady-State Gain),也常被称为直流增益(DC Gain),描述的是当一个稳定的系统在受到一个恒定的输入信号(阶跃输入)作用后,其输出达到一个新的稳定状态时,输出的稳态值与输入值之比。它衡量了系统对一个持续不变的输入的最终放大或缩小能力。
-
当我们考虑系统的稳态增益时,我们通常分析的是系统对单位阶跃输入 u(t)的稳态响应(即 t→∞ 时的响应,后面会提到),即稳态输出与阶跃输入之比。
-
显而易见,系统输出的 Laplace 变换为 Y(s)=G(s)U(s)=G(s)s1
-
假设考虑的系统稳定(稳定的系统才有稳态,才能计算稳态增益),我们可以利用终值定理来计算系统输出的稳态值
yss=t→∞limy(t)=s→0limsY(s)=s→0limsG(s)s1=s→0limG(s)=G(0)
-
我们得到了系统对单位阶跃输入的稳态输出值(稳态输出与阶跃输入之比)yss=G(0)
-
从物理意义上看,令 s=0 相当于在频域中考察系统对频率为零的信号的响应(σ=0,jω=0)。频率为零的信号正是一个恒定不变的直流信号,这与我们在时域中用来测试稳态增益的阶跃输入信号的最终状态是完全一致的。
4. 脉冲响应函数 (Impulse-Response Function)
- 定义:在零初始条件下,系统对单位脉冲输入 δ(t) 的响应,记为 g(t)。
- 与传递函数的关系:由于单位脉冲函数 δ(t) 的拉氏变换为1,所以输出量的Laplace变换为 Y(s)=G(s)
- 系统的脉冲响应函数 g(t) 是系统传递函数 G(s) 的拉普拉斯反变换。g(t)=L−1[G(s)]
- 反之,传递函数 G(s) 是脉冲响应函数 g(t) 的拉普拉斯变换。G(s)=L[g(t)]
- 权函数:脉冲响应函数 g(t) 也被称为系统的权函数。
- 线性定常系统的传递函数与脉冲响应函数包含系统动态特性的相同信息。(可以粗略认为,两者是等价的)
- 通过脉冲输入信号激励系统并测量系统的响应,能够获得有关系统动态特性的全部信息。
- 在实际中,当系统的时间常数较大时,持续时间很短的脉动输入信号可以看作脉冲输入信号。
5. 卷积积分 (Convolution Integral)
-
系统对于任意输入信号 x(t) 的输出响应 y(t) 可以通过输入与系统的脉冲响应函数 g(t) 的卷积来计算。
y(t)=∫0tx(τ)g(t−τ)dτ=∫0tg(τ)x(t−τ)dτ
2.3 自动控制系统方框图
1. 基本概念
- 方框图 (Block Diagrams):用方框表示系统元件功能,用带箭头的线表示信号流向的图解表示。
- 基本元件:
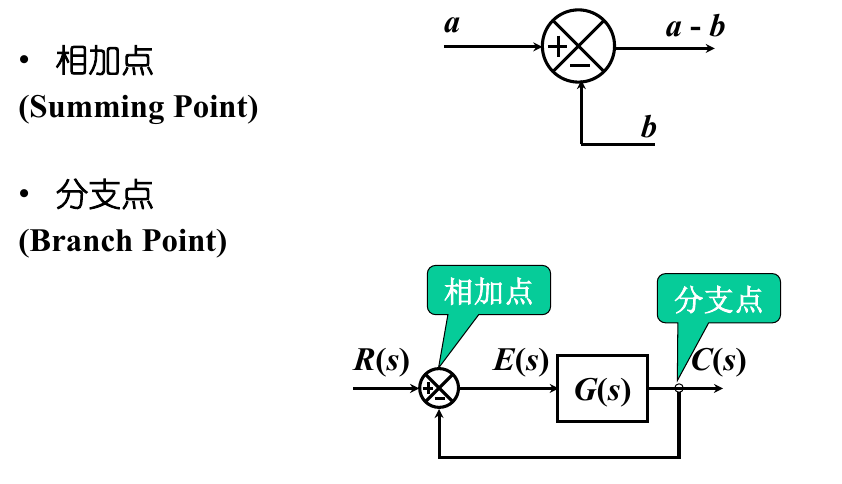
- 相加点 (Summing Point):对信号进行加减运算。
- 分支点 (Branch Point):将一个信号引向多个路径。
![image-20250924135550596]()
2. 闭环系统常用传递函数
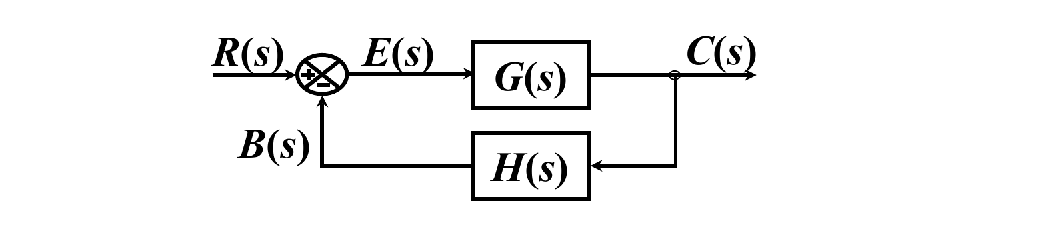
对于一个标准负反馈系统:
![image-20250924135838546]()
-
开环传递函数 (Open-Loop Transfer Function):反馈信号 B(s) 与误差信号 E(s) 之比。
-
前向传递函数 (Feed-forward Transfer Function):输出量 C(s) 与误差信号 E(s) 之比。
Gforward(s)=E(s)C(s)=G(s)
-
闭环传递函数 (Closed-Loop Transfer Function):输出量 C(s) 与输入量 R(s) 之比。
-
闭环系统的输出量取决于闭环传递函数和输入量(注意:此处假设为负反馈,若为正反馈,分母符号需改变 1−G(s)H(s) )
C(s)=Gclosed(s)R(s)=1+G(s)H(s)G(s)R(s)
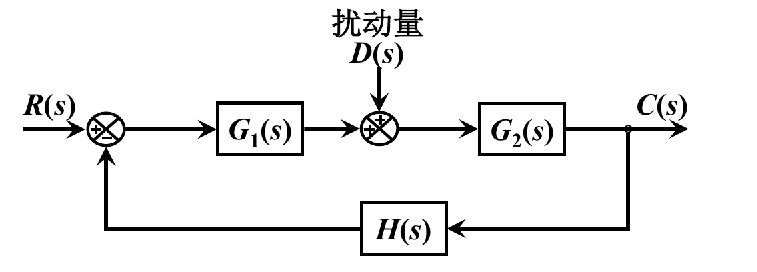
3. 带扰动的闭环系统
![image-20250924140601354]()
对于线性系统,可以应用叠加原理。系统的总输出是参考输入和扰动输入单独作用时产生的输出之和。
-
扰动作用下的输出 (R(s)=0):
-
当 ∣G1(s)H(s)∣≫1 和 ∣G1(s)G2(s)H(s)∣≫1 时,扰动量的闭环传递函数D(s)CD(s) 几乎等于零,扰动的影响被抑制
CD(s)=1+G1(s)G2(s)H(s)G2(s)D(s)
-
参考输入作用下的输出 (D(s)=0):
-
当 ∣G1(s)G2(s)H(s)∣≫1 时,参考输入量的闭环传递函数 R(s)CR(s)≈H(s)1 ,与 G1(s) 和 G2(s) 无关,只与 H(s) 成反比关系
-
也就是说,G1(s) 和 G2(s) 的变化不影响闭环传递函数 R(s)CR(s)
CR(s)=1+G1(s)G2(s)H(s)G1(s)G2(s)R(s)
-
总输出: 根据叠加原理
C(s)=CR(s)+CD(s)=1+G1(s)G2(s)H(s)G1(s)G2(s)R(s)+G2(s)D(s)≈H(s)1
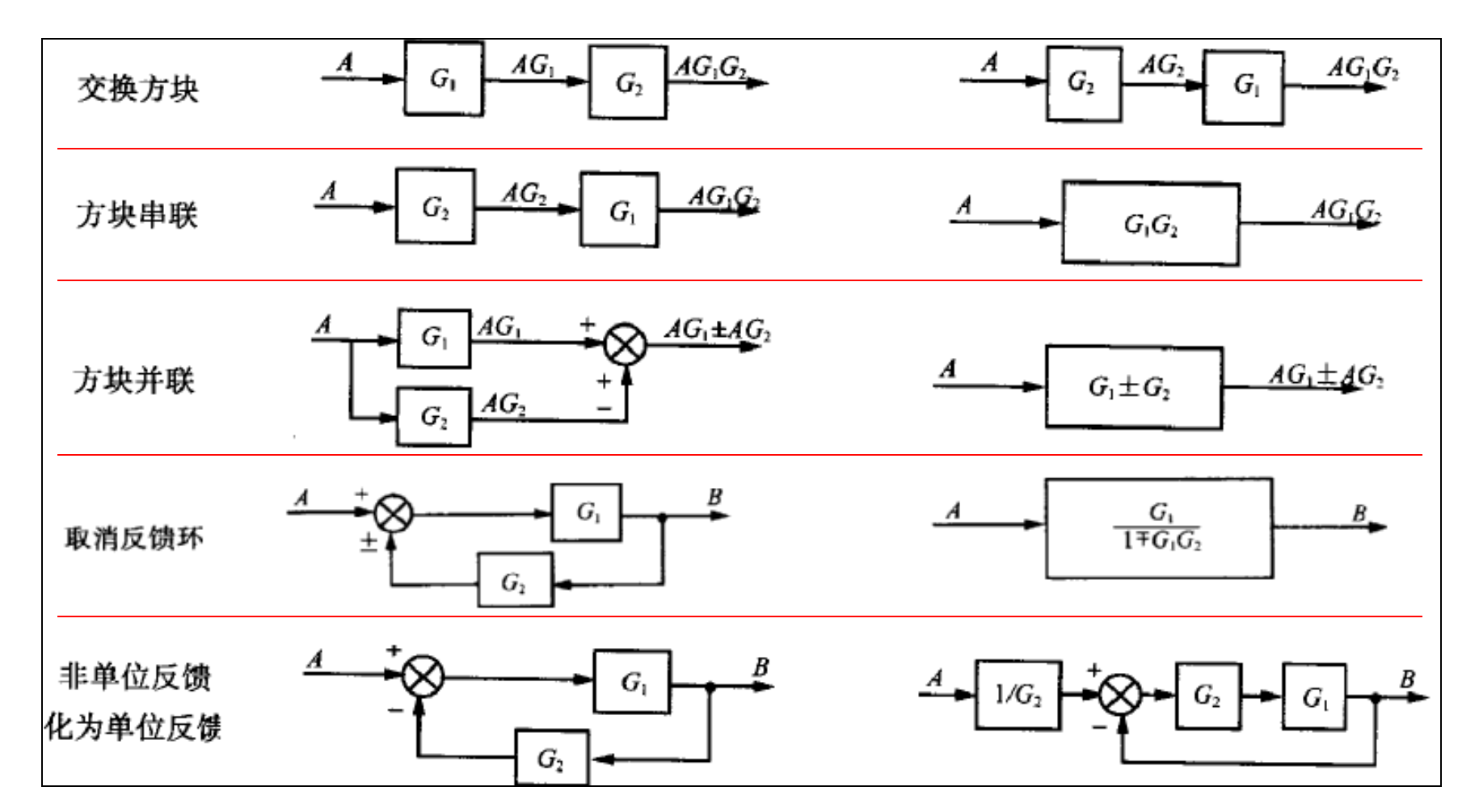
4. 方框图的简化与等效变换
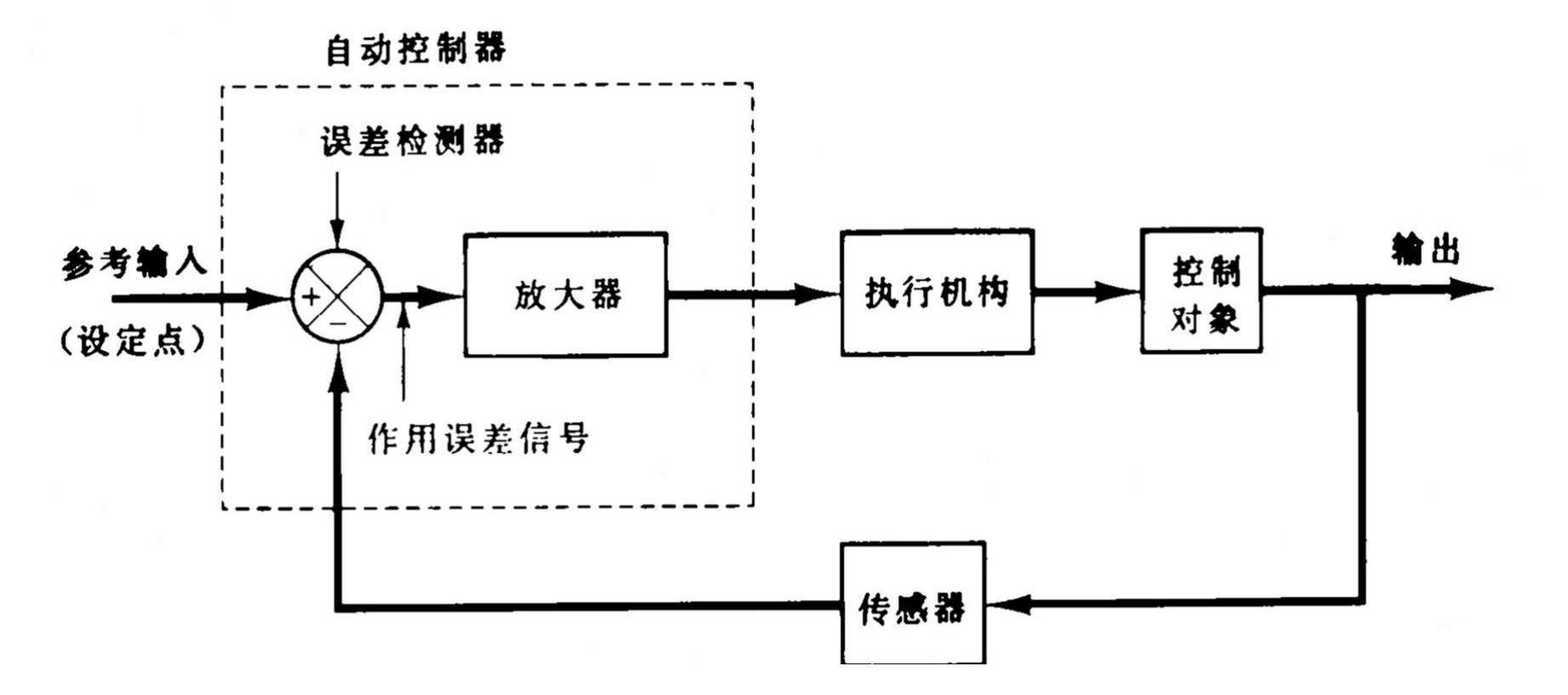
自动控制器的基本结构框图
![image-20250924150008063]()
-
基本原则:变换过程中,系统输入输出的等效关系不变。具体来说:
- 前向通路中传递函数的乘积必须保持不变。
- 回路中传递函数的乘积必须保持不变。
-
常用法则:
- 串联:G(s)=G1(s)G2(s)
- 并联:G(s)=G1(s)±G2(s)
- 反馈环消除:G(s)=1∓G1(s)H(s)G1(s)
- 非单位反馈化为单位反馈:输入信号变为原来的 G21,误差信号变为原来的 G2
-
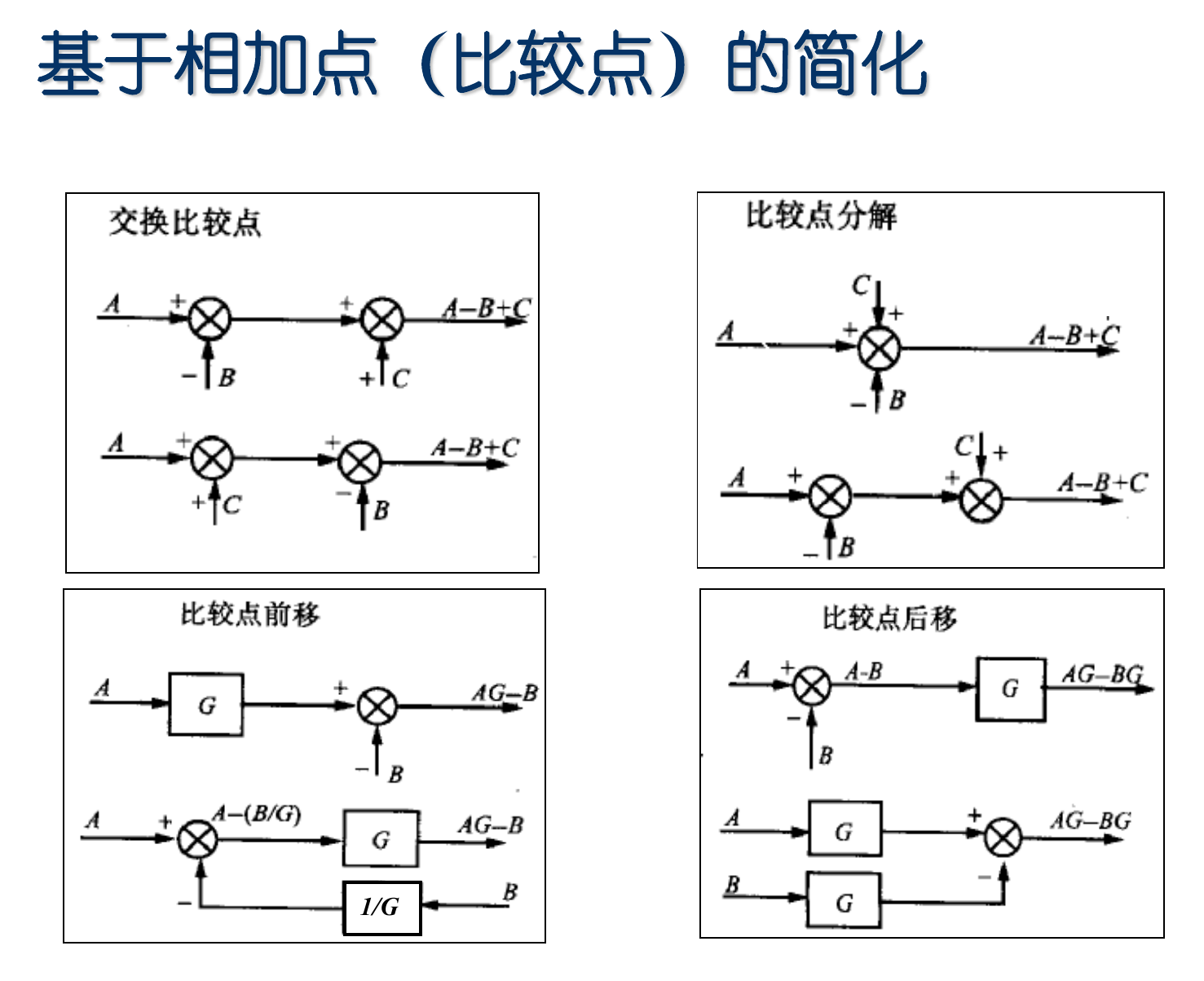
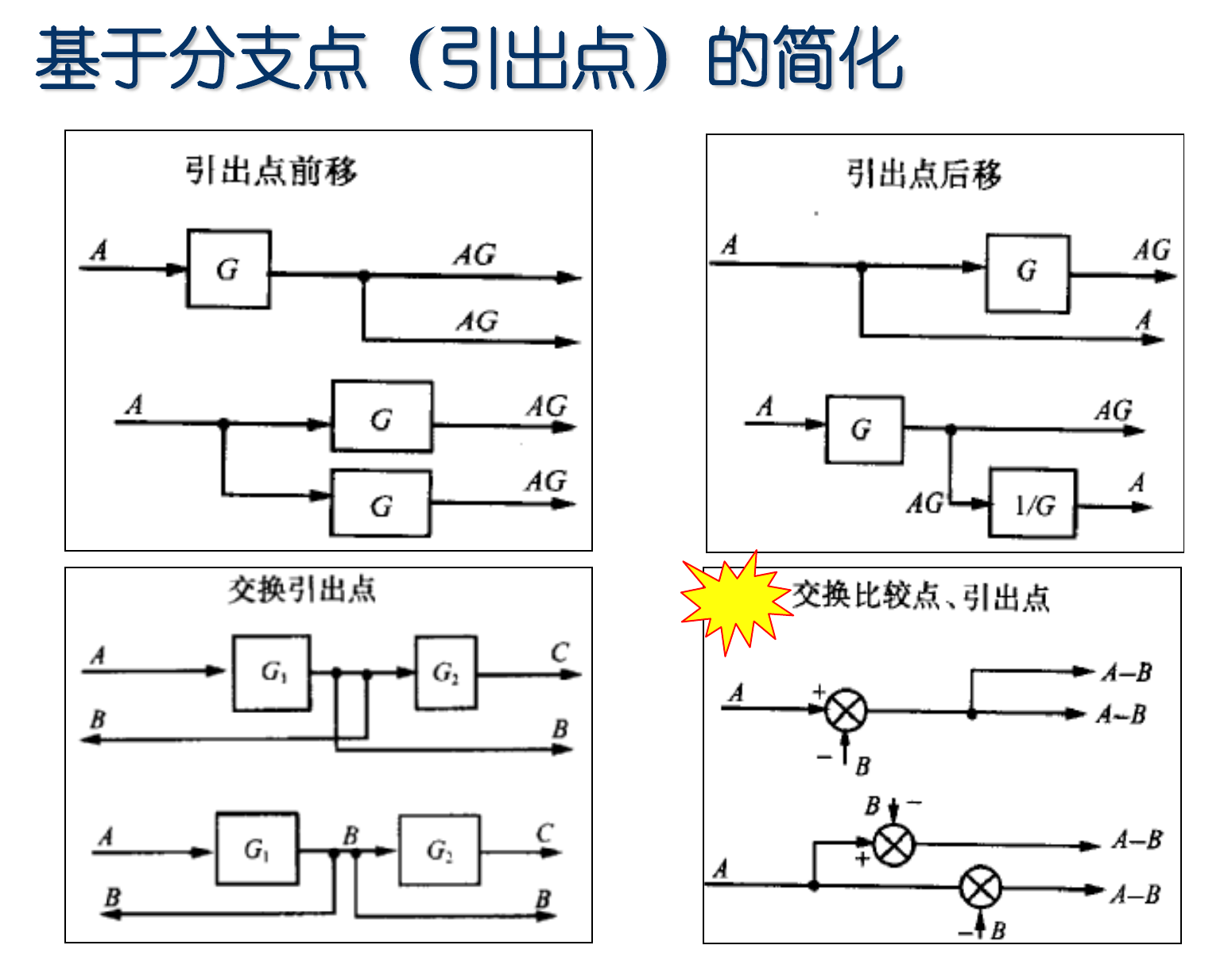
交换/分解相加点(比较点)、交换分支点:直接操作就行,一般不需要补偿
-
==交换比较点和引出点:==引出点前移到比较点之前,需要在两条支路上都添加相应的比较点
-
相加点/分支点的移动(前移/后移):移动时需引入补偿环节(对相应通路添加补偿系数)以保证等效性。
![image-20250924150232188]()
![image-20250924214155771]()
![image-20250924214217238]()
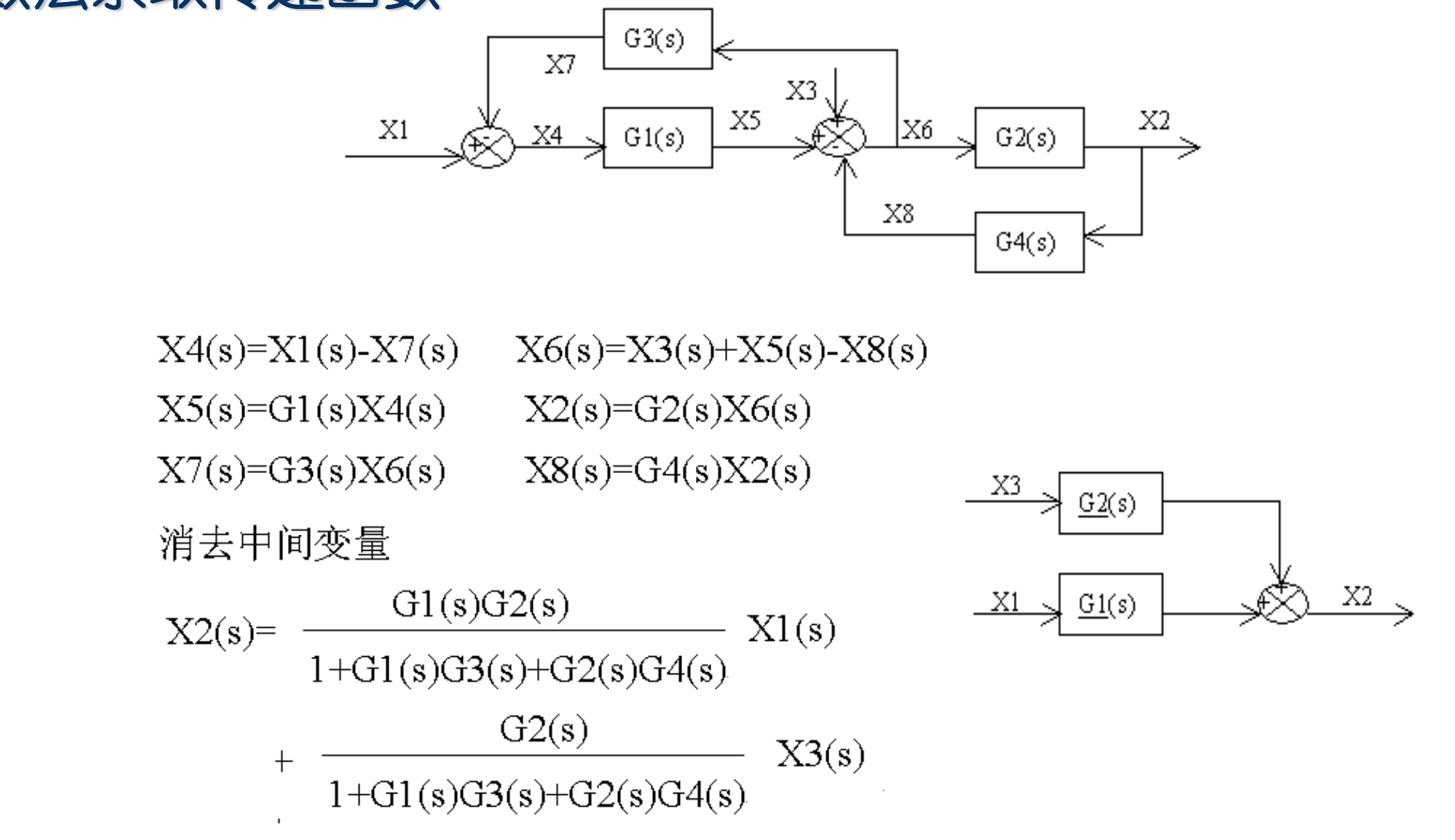
- 当然也可以代数法求传递函数
- 对于复杂的系统,代数法计算很繁琐,不太能手算,只适合用计算机处理
![image-20250924221030954]()
单前向通路多回路的增益
只有一条前向通道,回路互相接触,前向通道与回路接触 的多回路系统的闭环传递函数
Φ(s)=1−∑i=1nGBi(s)GA(s)
- GA(s): 前向通路传递函数的乘积。
- GBi(s): 每个反馈回路的传递函数的乘积,注意包含的加和点的符号 (+正反馈 - 负反馈)。
- n: 闭环系统所具有的反馈回路的总数
- i: 各反馈回路的序号
完整的梅逊公式
用于复杂系统,直接从信号流图(或方框图)求取总传递函数。
G(s)=Δ1k=1∑NPkΔk
-
Pk:第 k 条前向通路的增益。带符号计算!
-
Δ:系统特征式
Δ=1−(∑Li)+(∑LiLj)−(∑LiLjLk)+⋯+(−1)m∑L(m)
- ∑Li:所有独立回路传递函数之和。
- ∑LiLj:所有互不接触的两两回路的传递函数乘积之和。
- ∑LiLjLk:所有互不接触的三个回路的传递函数乘积之和,以此类推。
- L(m): 所有互不接触的 m 个回路的增益乘积之和
- 注意:所有回路增益带符号计算! (+正反馈 - 负反馈)
-
Δk:Δ 中除去与第 k 条前向通路相接触的回路(置0或者直接去掉相关项)后剩余部分的值。
-
不难发现,由Mason公式可以得到整个系统的特征方程是 Δ=0
- 所以,有结论:从方框图的角度来看,系统的极点仅由系统结构(回路的结构)决定,与取哪个量作为输入输出无关!
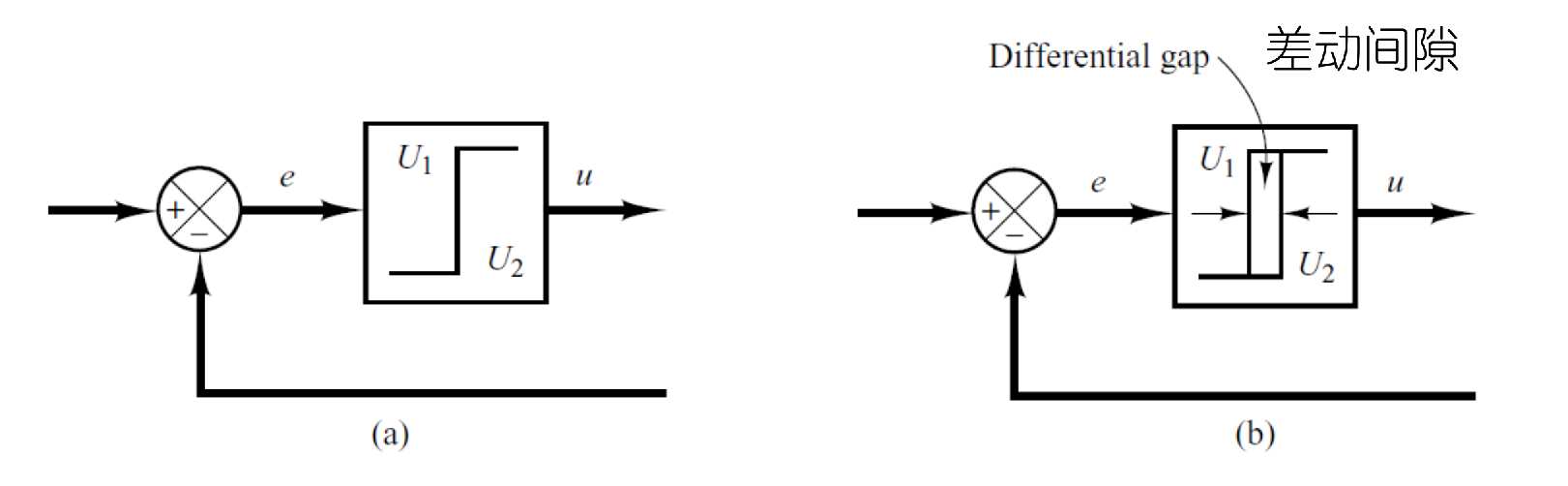
6. 工业控制器分类
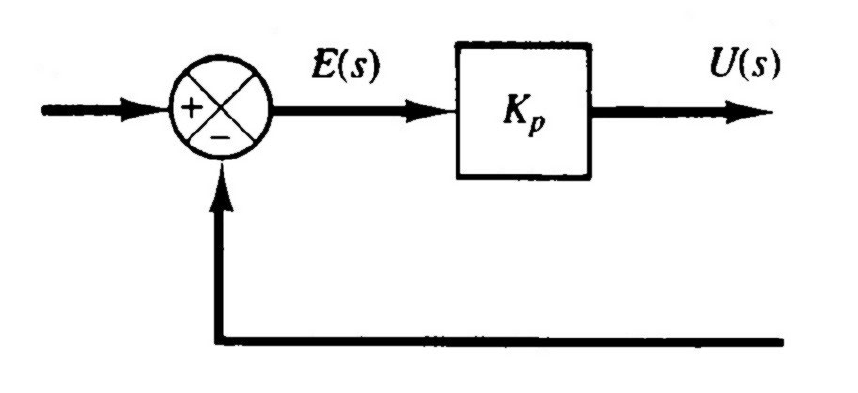
![image-20251222204030290]()
- 积分控制器 (I): 时域表达 u(t)=Ki∫e(t)dt,传递函数 G(s)=sKi
- 积分控制器可以消除一阶被控对象在阶跃输入下的稳态误差(注意:需要明确被控对象阶数和)
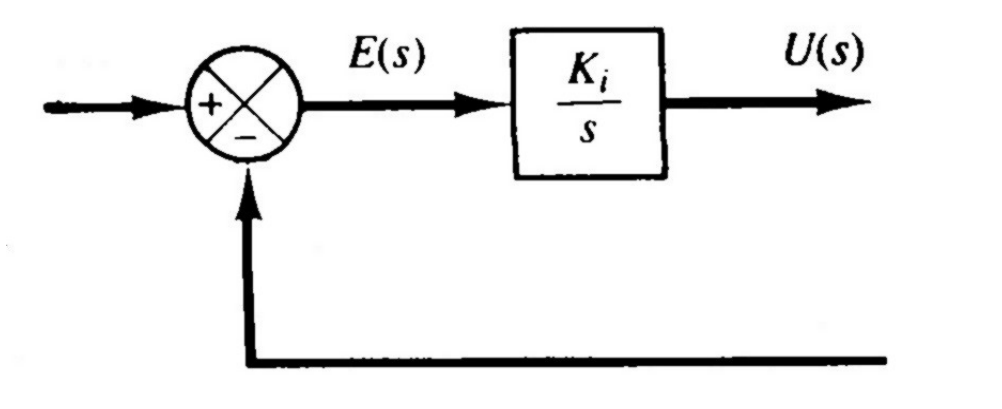
![image-20251222204335068]()
- 比例-积分控制器 (PI): 时域表达 u(t)=Kpe(t)+TiKp∫0te(t)dt,传递函数 G(s)=Kp(1+Tis1)
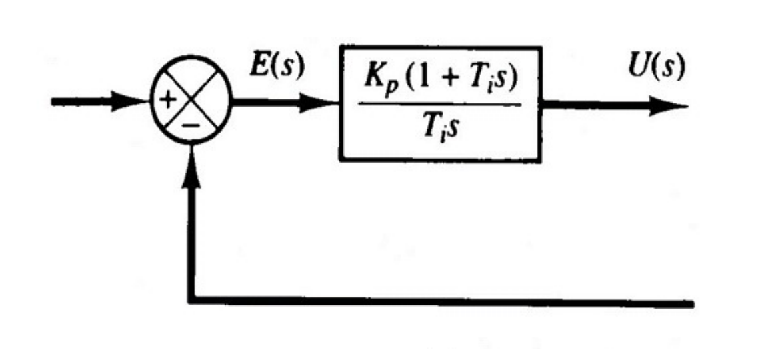
![image-20251222204716176]()
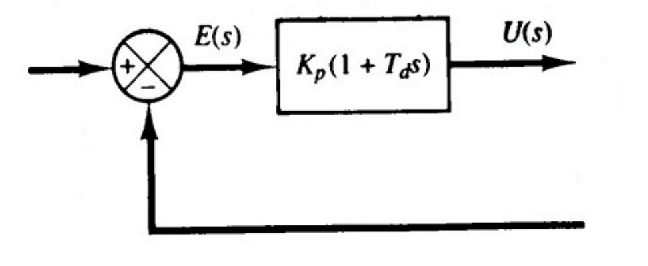
- 比例-微分控制器 (PD): 时域表达 u(t)=Kpe(t)+KpTddtde(t) ,传递函数 G(s)=Kp(1+Tds)
![image-20251222204947598]()
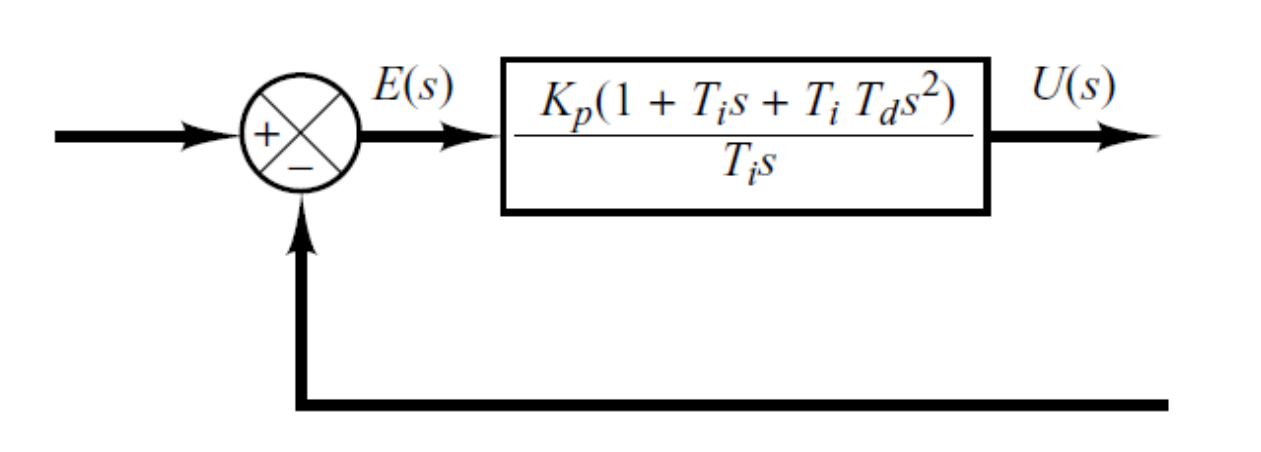
- 比例-积分-微分控制器 (PID): 时域表达 u(t)=Kpe(t)+TiKp∫0te(t)dt+KpTddtde(t),传递函数 G(s)=Kp(1+Tis1+Tds)
![image-20251222205006732]()
2.4 状态空间模型
1. 现代控制理论 vs. 传统控制理论
- 现代控制理论:
- 研究对象:多输入多输出(MIMO),线性和非线性,定常或时变系统。系统初始状态可以不为0。
- 分析方法:时域分析,基于状态空间模型。
- 传统控制理论:
- 研究对象:单输入单输出(SISO),线性的定常系统,一般默认状态为0(只研究零状态响应)。
- 分析方法:复频域分析,基于传递函数。
2. 状态空间基本概念
- 状态 (State):完全表征系统行为的最小一组变量。只要知道了在 t=t0 时的一组变量和 t≥t0 时的输入量,就能够完全确定系统在任何时间 t≥t0 时的行为。
- 状态变量 (State Variables):构成系统状态的最小一组变量。如果至少需要 n 个变量才能完全描述动态系统的行为,则这 n 个变量就是一组状态变量。
- 状态向量 (State Vector):由状态变量构成的 n 维列向量 x。
- 状态空间 (State Space):以所有状态变量为坐标轴构成的 n 维空间。
- 对于一个系统来说,无论怎么选状态变量,状态变量数(即状态向量的维度,状态空间的维度)都相同,等于系统中积分器的数目,也等于系统的阶数
- 一般来说,选择状态变量的原则:
- 状态变量数等于系统的阶数
- 选择每个积分器(或者延迟积分器)的输出作为状态变量
3. 状态空间方程
- 虽然对于同一个系统来说,状态变量数一般是固定的,但选择的具体状态变量可以不同,故状态空间表达式不唯一
一般的状态空间方程由状态方程和输出方程组成(考试时不要漏写输出方程)
{x˙(t)=f(x,u,t)y(t)=g(x,u,t)State Eq.Output Eq.
对于线性系统,状态空间方程可以线性化为矩阵形式
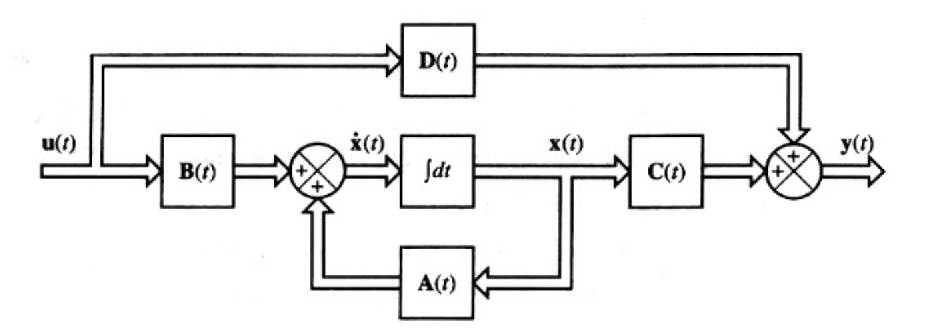
{x˙(t)=A(t)x(t)+B(t)u(t)状态方程y(t)=C(t)x(t)+D(t)u(t)输出方程
线性定常系统的状态空间模型由状态方程和输出方程组成:
{x˙(t)=Ax(t)+Bu(t)(状态方程)y(t)=Cx(t)+Du(t)(输出方程)
- x(t): 状态向量 (n×1)
- u(t): 输入向量 (r×1)
- y(t): 输出向量 (m×1)
- A: 状态矩阵 (n×n)
- B: 输入矩阵 (n×r)
- C: 输出矩阵 (m×n)
- D: 直接传输矩阵 (m×r)
![image-20250928112259422]()
4. 传递函数与状态空间模型的关系
过程:对状态空间方程进行Laplace变换
{sX(s)−x(0)=AX(s)+BU(s)Y(s)=CX(s)+DU(s)
令初始条件为0
sX(s)=AX(s)+BU(s)⟹(sI−A)X(s)=BU(s)⟹X(s)=(sI−A)−1BU(s)
代入输出方程,得到
Y(s)=[C(sI−A)−1B+D]U(s)
从而得到传递函数
G(s)=C(sI−A)−1B+D
其中 I 是单位矩阵。
-
特征方程是 ∣sI−A∣=0 ,即系统极点就是状态矩阵 A 的特征值。
-
可以得出结论:系统极点只与状态矩阵 A 有关(故有时 A 也被称为系统矩阵)
-
对于有r个输入量和m个输出量的MIMO系统,上式给出的将是 mxr 形状的传递矩阵 (Transfer Matrix) G(s)=[Gi,j(s)]m×r。
- 传递矩阵给出了从输入向量到输出向量的传递关系,即所有输入量到所有输出量的传递函数 Y(s)=G(s)U(s)
5. 由系统微分方程建立状态空间模型
情况一:输入端无微分项
系统方程:y(n)+a1y(n−1)+⋯+any=u
选择状态变量为
x1x2xn=y=y˙…=y(n−1)
从而容易得到
x˙1x˙2x˙n−1=x2=x3…=xn
最高阶状态变量的状态方程需要通过系统方程得到
x˙n=y(n)=−any+⋯−a1y(n−1)+u=−anx1−⋯−a1xn+u⟹x˙n=−anx1−⋯−a1xn+u
整理成矩阵形式可得可控标准型:状态方程为
x˙=Ax+Bu
其中
A=0⋮0−an1⋮0−an−1…⋱……0⋮1−a1,B=0⋮01
输出方程为
y=Cx
其中
C=[10…0],D=0
情况二:输入端有微分项
系统方程:y(n)+⋯+any=b0u(n)+⋯+bnu
使用特定变量代换可得到与情况一相同的 A 和 C 矩阵,但 B 和 D 矩阵不同,其元素由系统的 ai 和 bi 系数共同决定。
假设
x1x2x3⋮xn=y−β0u=x˙1−β1u=y˙−β0u˙−β1u=x˙2−β2u=y¨−β0u¨−β1u˙−β2u=x˙n−1−βn−1u=y(n−1)−β0u(n−1)−β1u˙(n−1)−⋯−βn−2u˙−βn−1u
我们希望这样一组状态变量代入系统方程后可以消除所有输入项的导数,所以可以得到式中的系数
β0β1β2β3⋮βn=b0=b1−a1β0=b2−a1β1−a2β0=b3−a1β2−a2β1−a3β0=bn−a1βn−1−⋯−an−1β1−anβ0
从而容易得到
x˙1x˙2x˙n−1=x2+β1u=x3+β2u⋮=xn+βn−1u
对于最高阶的状态变量,状态方程需要使用定义式求导,代入系统方程然后经过非常复杂的代数化简得到
x˙n=−anx1−an−1x2−⋯−a1xn+βnu
整理成矩阵形式,得到最后的结论:
{x˙=Ax+Buy=Cx+Du
其中 x=x1x2⋮xn−1xn A=00⋮0−an10⋮0−an−101⋮0−an−2⋯⋯⋱⋯⋯00⋮1−a1 B=β1β2⋮βn−1βn
C=[10⋯0] D=β0=b0
6. 从传递函数建立状态空间的方法
- 如果题目要求使用给定的状态变量,需要先把传递函数Laplace逆变换回时域,然后仿照上一小节的方法,使用给定的状态变量建立状态方程和输出方程。
- 如果题目没有要求使用特定的状态变量,更建议用后面的可控标准型/可观标准型,代入传递函数的分子分母的各幂次系数,直接获得状态空间模型,无需计算,更简便。
7. 从方框图建立状态空间模型的方法
第一步:选择状态变量
-
必要的预处理
- 大于等于2阶的积分器全部拆成一阶
- 含微分器和积分器的项先进行出发,分离出一个常数项和积分器,然后处理成并联支路。
-
在方框图中,找到所有的积分器环节(在拉普拉斯域中表示为 1/s)。
-
将每一个积分器的输出定义为一个状态变量 xi(t)。
-
如果有 n 个积分器,那么系统就有 n 个状态变量,状态向量 x(t) 的维度就是 n。
为什么这么选? 因为积分器的输出代表了系统“记忆”或能量存储的状态。其导数 x˙i(t) 恰好就是该积分器的输入,这完美地构建了状态方程中 x˙ 与其他变量的关系。
第二步:建立状态方程
- 对每一个状态变量 xi(t),写出其一阶微分方程 x˙i(t)=…。
- 根据方框图,找到对应积分器的输入信号。
具体来说:
- 对于一阶积分器来说,这个输入信号就是 x˙i(t)
s1Xinput(s)=Xi(s)⟶L−1x˙i(t)=xinput(t)
- 对于一阶延迟积分器,情况略微复杂一些
- 这种情况理论上也可以通过把一阶延迟积分器分解成一个反馈网络来处理。
s+a1Xinput(s)=Xi(s)⟹Xinput(s)=sXi(s)+aXi(s)⟶L−1x˙i(t)=xinput(t)−axi(t)
接着:
- 将这个输入信号表示为系统输入 u(t) 和所有状态变量 x(t) 的线性组合。
- 你需要从积分器的输入端开始,沿着信号线反向追溯,经过的求和点(Summing Junction)和增益模块(Gain Block)都会影响这个表达式。
- 为所有 n 个状态变量重复此过程,你将得到 n 个一阶微分方程。
第三步:建立输出方程
- 找到方框图的最终输出信号 y(t)。
- 将输出信号 y(t) 表示为系统输入 u(t) 和所有状态变量 x(t) 的线性组合。
- 与上一步类似,从输出点反向追溯信号路径,确定其由哪些状态变量和输入信号组合而成。
第四步:整理成矩阵形式
-
对于状态方程:将第二步得到的 n 个关于 x˙i(t) 的方程组写成矩阵形式 x˙=Ax+Bu。
- 矩阵 A 的元素 aij 是状态方程中 xj 对 x˙i 的贡献系数。
- 矩阵 B 的元素 bik 是状态方程中输入 uk 对 x˙i 的贡献系数。
-
对于输出方程:将第三步得到的关于 y(t) 的方程写成矩阵形式 y=Cx+Du。
- 矩阵 C 的元素 cij 是输出方程中 xj 对输出 yi 的贡献系数。
- 矩阵 D 的元素 dik 是输出方程中输入 uk 对输出 yi 的直接贡献系数(如果输入信号没有经过任何积分器直接连接到输出,则 D 非零)。对于大多数物理系统,D 矩阵通常是零矩阵。
![image-20251011173903858]()