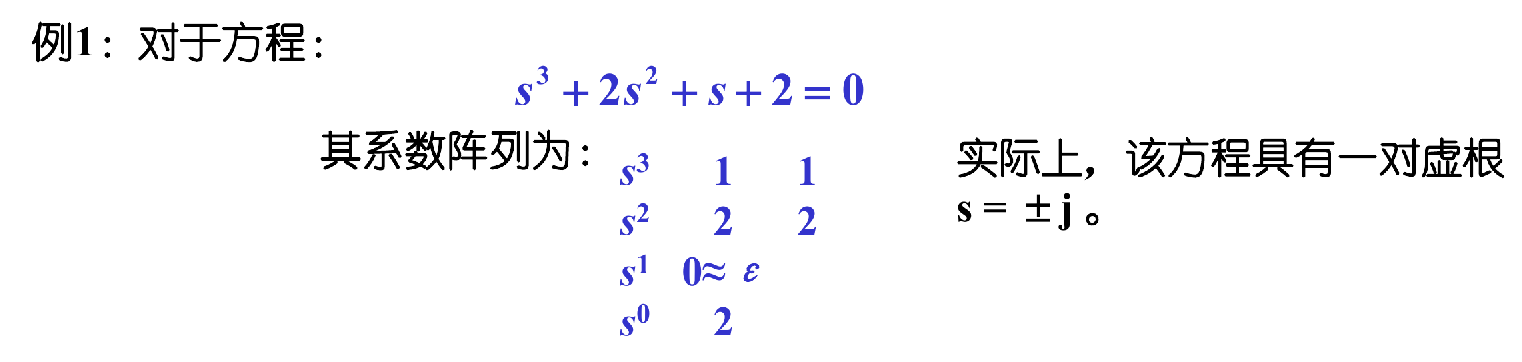第五章 瞬态响应和稳态响应分析
本章主要内容涵盖了控制系统动态性能的核心概念,包括:
- 引言
- 一阶、二阶及高阶系统的时域分析
- 劳斯稳定判据
- 积分和微分控制对系统性能的影响
- 单位反馈控制系统中的稳态误差
5.1 引言
- 系统性能分析:基于系统的数学模型,可以采用多种方法分析其性能。
- 试验输入信号:在分析和设计控制系统时,通常会预先规定一些特殊的试验输入信号,通过比较系统对这些信号的响应来评估其性能特点。
- 设计准则:许多设计准则都建立在系统对这些特殊测试信号的响应,或是对初始条件变化的响应之上。
5.1.1 典型试验信号
为了分析系统的特性,常采用以下几种典型的输入信号:
- 阶跃函数 (Step functions):模拟系统输入突然发生的变化。 r(t)=u(t)
- 斜坡函数 (Ramp functions):模拟系统输入以恒定速度变化。
- 加速度函数 (Acceleration functions):模拟系统输入以恒定加速度变化。
- 脉冲函数 (Impulse functions):模拟系统受到瞬时冲击。
- 正弦函数 (Sinusoidal functions):用于分析系统的频率特性。
核心思想:采用何种信号取决于系统在正常工作中最常见的输入信号形式。
5.1.2 瞬态响应和稳态响应
控制系统的总输出响应 c(t) 可以分解为两部分:瞬态响应 ct(t) 和稳态响应 cs(t)。
c(t)=ct(t)+cs(t)
5.1.3 绝对稳定性、相对稳定性和稳态误差
- 绝对稳定性 (Absolute Stability):判断系统是稳定还是不稳定。
- 稳定:系统受到扰动后,能恢复到原来的平衡状态。
- 临界稳定:系统受到扰动后,在新的位置持续振荡,不发散也不收敛。
- 不稳定:系统受到扰动后,响应发散。
- 系统的稳定性取决于特征根(极点)在复平面上的位置(回顾一下信号与系统的知识)
- 特征根全部在左半平面:系统绝对稳定
- 特征根在虚轴上:系统临界稳定,最终呈等幅振荡状态
- 特征根在右半平面:系统不稳定
- 相对稳定性 (Relative Stability):衡量系统稳定的程度,即系统暂态响应衰减的速度。
- 稳态误差 (Steady-State Error):系统进入稳态后,期望输出与实际输出之间的差值。
5.2 一阶系统 (First-Order Systems)
![image-20251224124848854]()
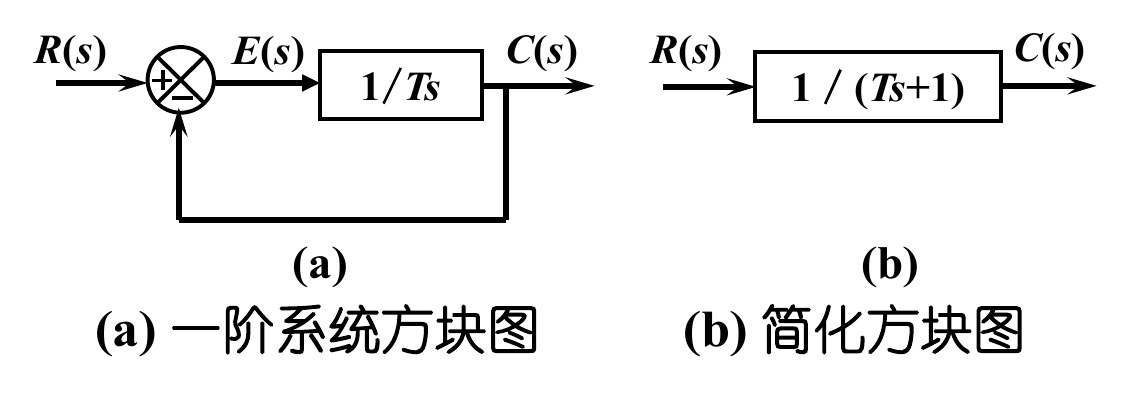
一阶系统由以下方框图表示,其输入/输出关系(传递函数)为:
传递函数:
R(s)C(s)=Ts+11
其中,T 是系统的时间常数。
5.2.1 一阶系统的单位阶跃响应
![image-20251124184924297]()
当输入为单位阶跃信号时,R(s)=s1。
输出 C(s) 为:
C(s)=Ts+11⋅s1=s(Ts+1)1
通过拉氏反变换,得到时域响应:
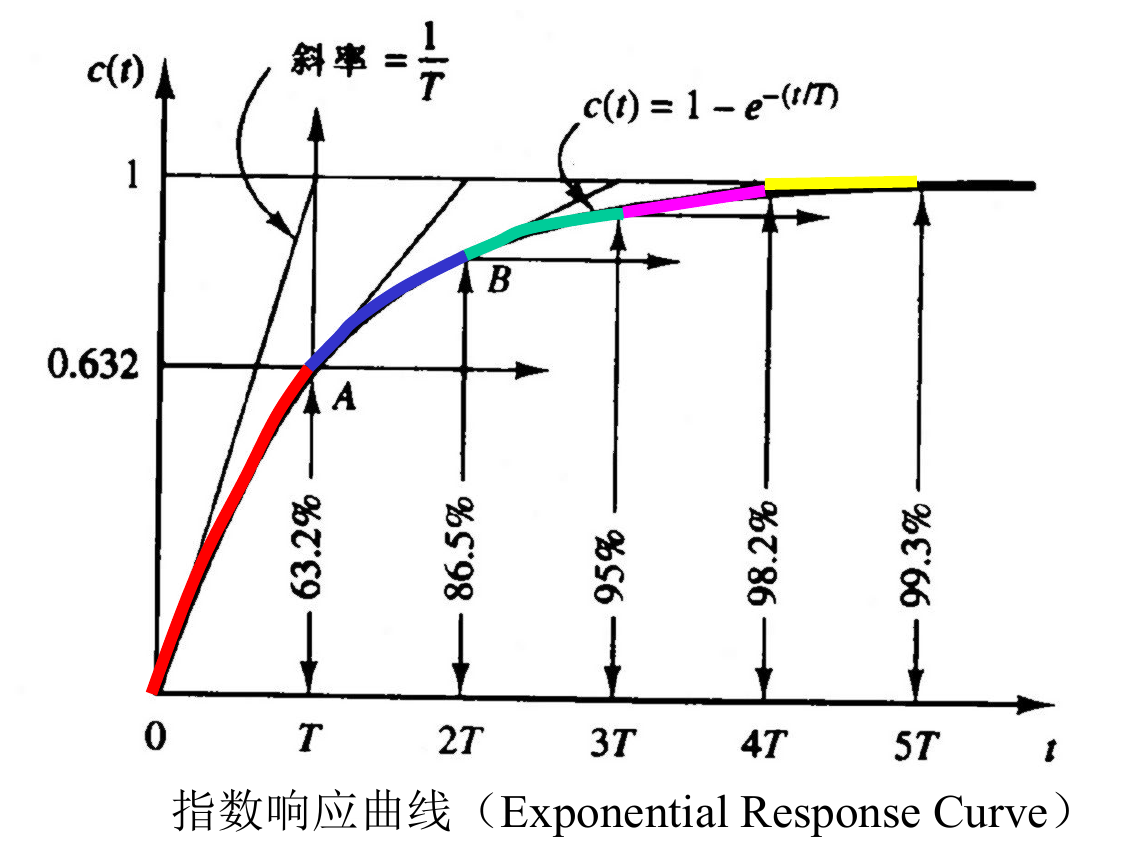
c(t)=1−e−t/T,t≥0
响应特性:
- 初始值:c(0)=0。
- 终值:limt→∞c(t)=1。
- 当 t=T (一个时间常数) 时,响应达到终值的 63.2%,即 c(T)=1−e−1≈0.632。
- 在 t=0 处的初始斜率为 dtdc(t)∣t=0=T1。(初始斜率表征了初始响应速度)
- 时间常数决定了响应速度
5.2.2 一阶系统的单位斜坡响应
![image-20251124184954079]()
当输入为单位斜坡信号时,r(t)=t,其拉氏变换为 R(s)=s21。
输出 C(s) 为:
C(s)=Ts+11⋅s21=s21−sT+Ts+1T2
通过拉氏反变换,得到时域响应:
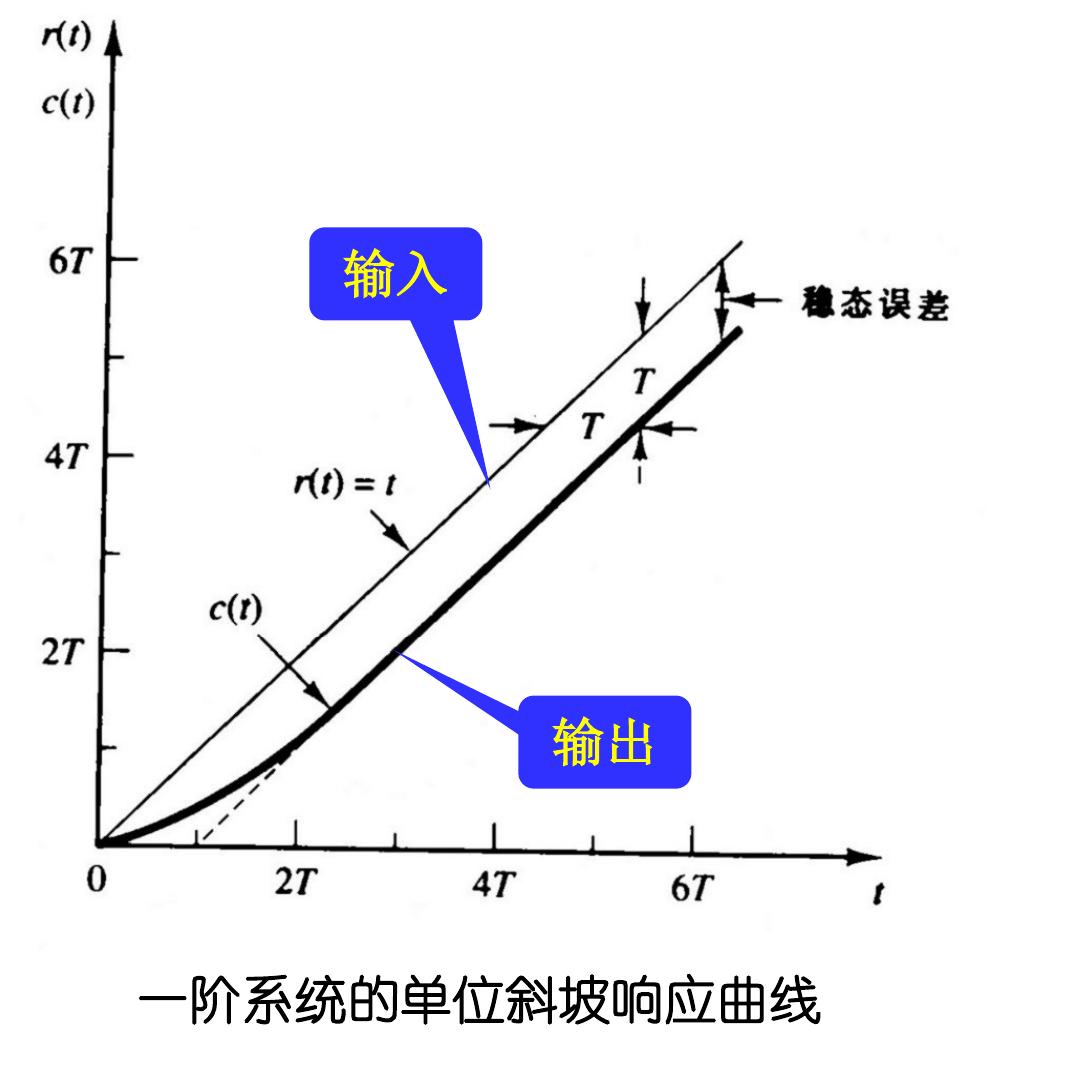
c(t)=t−T+Te−t/T,t≥0
误差信号 e(t)=r(t)−c(t) 为:
e(t)=T(1−e−t/T)
稳态误差 ess 为:
ess=t→∞lime(t)=T
5.2.3 一阶系统的单位脉冲响应
当输入为单位脉冲信号时,R(s)=1。
输出 C(s) 为:
C(s)=Ts+11
通过拉氏反变换,得到时域响应:
c(t)=T1e−t/T,t≥0
5.2.4 线性定常系统的重要特性
对于线性定常系统,输出的导数等于系统对输入导数的响应。
- 单位阶跃响应是单位脉冲响应的积分。
- 单位斜坡响应是单位阶跃响应的积分。
5.3 二阶系统 (Second-Order Systems)
![image-20251014221450305]()
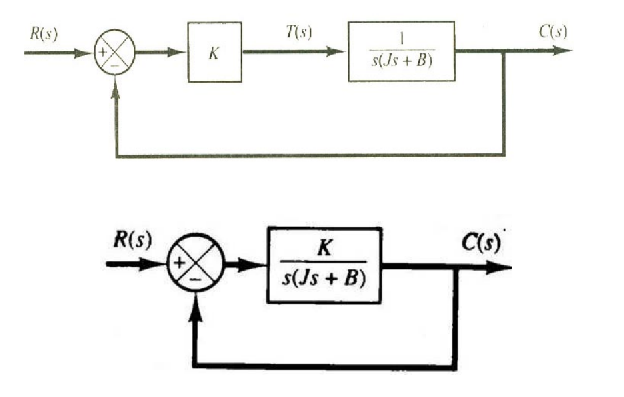
一个单位负反馈二阶系统的闭环传递函数为
- 我们只研究无零点,分子为常数的二阶系统,分子含s的二阶系统有很大不同,请参见其他教材
- 单位负反馈系统的稳态增益是1,如果是反馈回路系数变成 KH ,稳态增益会变成 KH1 ,但其响应特性是不变的,这边的结论仍然能成立。
R(s)C(s)=Js2+Bs+KK
为了研究方便,令
JK=ωn2,JB=2ζωn=2σ
标准的二阶系统(无零点)闭环传递函数为:
R(s)C(s)=s2+2ζωns+ωn2ωn2
![image-20251224125056083]()
重要参数定义:
-
ωn:无阻尼自然频率 (undamped natural frequency)。
-
ζ:阻尼比 (damping ratio)。
ζ=BcB=2JKB
-
σ=ζωn:衰减系数 (attenuation),也叫衰减率。
由闭环传递函数,可知标准二阶系统的特征方程为 s2+2ζωns+ωn2=0,判别式为 Δ=4ζ2ωn2−4ωn2=4ωn2(ζ2−1)
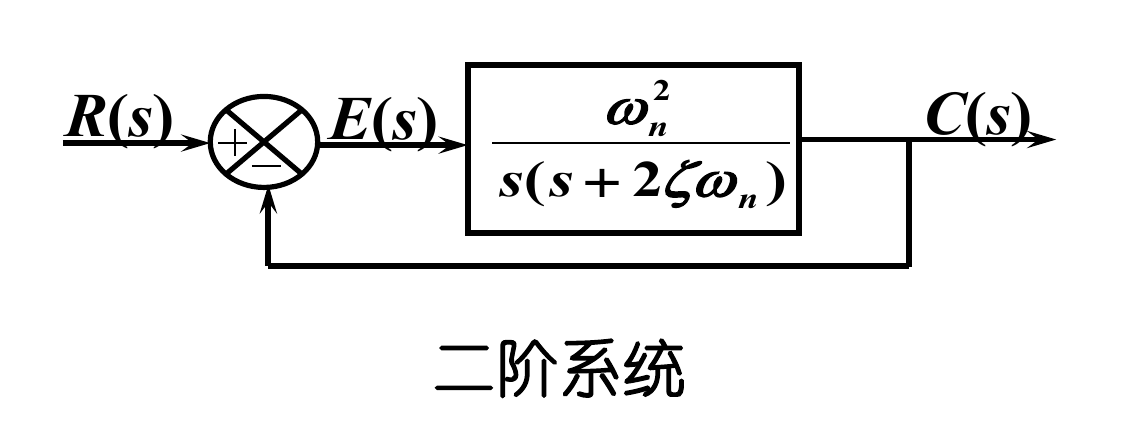
故根据阻尼比 ζ 的值,二阶系统的响应可以分为四种情况:
-
欠阻尼系统 (0<ζ<1):闭环极点为一对共轭复数,瞬态响应是振荡的。
R(s)C(s)=(s+ζωn+jωd)(s+ζωn−jωd)ωn2⟹pole:s1,2=−ζωn±jωd
其中,极点的实部(的绝对值) σ=ζωn 为衰减系数 ,极点的虚部 ωd=ωn1−ζ2 为阻尼自然频率。
-
临界阻尼系统 (ζ=1):闭环极点为两个相等的负实数,瞬态响应不振荡。
R(s)C(s)=(s+ωn)2ωn2⟹pole:s1,2=−ωn
-
过阻尼系统 (ζ>1):闭环极点为两个不等的负实数,瞬态响应不振荡。
R(s)C(s)=(s+ζωn+ωn1−ζ2)(s+ζωn−ωn1−ζ2)ωn2⟹pole:s1,2=−ζωn±1−ζ2ωn
-
无阻尼系统 (ζ=0):闭环极点为一对纯虚数,瞬态响应为等幅振荡。
R(s)C(s)=s2+ωn2ωn2=(s+jωn)(s−jωn)ωn2⟹pole:s1,2=±jωn
二阶系统对阶跃输入信号的响应
![image-20251009101348812]()
(1) 欠阻尼情况 (0<ζ<1)
-
复频域响应:
C(s)=(s2+2ζωn+ωn2)sωn2=s(s−s1)(s−s2)s1s2(s1,2=−ζωn∓jωd)=s1+s+ζωn+jωds1−s2s2+s+ζωn−jωds2−s1s1=s1−s+ζωn+jωd21+j2ωdζωn−s+ζωn−jωd21−j2ωdζωn
-
时域响应:
c(t)=L−1[C(s)]=1−(21+j2ωdζωn)e(−ζωn−jωd)t−(21−j2ωdζωn)e(−ζωn+jωd)t=1−e−ζωnt[2ejωdt+e−jωdt+ωdζωn2jejωdt−e−jωdt]=1−e−ζωnt(cosωdt+1−ζ2ζsinωdt)=1−1−ζ2e−ζωntsin(ωdt+β)where β=arctanζ1−ζ2=arccosζ
其中,ωd=ωn1−ζ2 为阻尼自然频率。
-
误差信号:e(t)=r(t)−c(t)=1−ζ2e−ζωntsin(ωdt+β) 是一个阻尼正弦振荡,稳态时误差为零,即 t→∞时,输入量与输出量之间不存在误差。
(2) 无阻尼情况 (ζ=0)
-
时域响应: 将 ζ=0 代入欠阻尼情况,可得
c(t)=1−cos(ωnt),t≥0
系统以无阻尼自然频率 ωn 进行等幅振荡。
-
对比欠阻尼和无阻尼情况,可以得到以下规律:
- 极点虚部的大小正好就是振荡频率
- 如果阻尼减小到零, 系统将以无阻尼自然频率 ωn 振荡。
- 现实中的系统总具有一定的阻尼,不可能通过试验观察到无阻尼自然频率。
- 可观察到的频率是阻尼自然频率 ωd, 它等于 ωd=ωn1−ζ2。该频率总是低于无阻尼自然频率。随着 ζ 值增大, 阻尼自然频率 ωd 将减小。如果 ζ 值增大到 1, 系统的响应将变成过阻尼的, 因而系统将不再产生振荡。
(3) 临界阻尼情况 (ζ=1)
-
时域响应:
c(t)=1−e−ωnt(1+ωnt),t≥0
响应是所有非振荡响应中最快的。
-
若闭环传递函数的两个极点接近相等,则系统可以近似地看作为临界阻尼系统。
(4) 过阻尼情况 (ζ>1)
-
复频域响应:
C(s)=(s+ζωn+ωn1−ζ2)(s+ζωn−ωn1−ζ2)sωn2=(s−s1)(s−s2)ss1s2=s−s1s1−s2s2+s−s2s1−s2s1+s1=s1−s21(s−s1s2+s−s2s1)+s1=2ωnζ2−1s1s2(s11s−s11+s21s−s21)+s1=2ζ2−1ωn(s11s−s11+s21s−s21)+s1
其中 s1,2=−(ζ∓ζ2−1)ωn 为系统的两个极点
-
时域响应:
c(t)=1+2ζ2−1ωn(s1e−s1t−s2e−s2t),t≥0
其中 s1,2=(ζ±ζ2−1)ωn 和系统的两个极点相对应(这边推导的时候和复频域那边的极点差了一个负号)。响应包含两个衰减的指数项,响应缓慢。
- 极点的位置决定了其对应的响应项的衰减速度,远离虚轴的极点对应的 es2t 衰减更快,靠近虚轴的极点 es1t 衰减较慢。因此,靠近虚轴的极点对系统性能的影响更大,称为系统的主导极点。
-
主导极点近似:
-
从时域来看,时域响应具有 c(t)=1+K1es1t+K2es2t 的形式。根据前面提到的近似原则,当ζ≫1时,可以丢掉 es2t 项,近似成 c(t)=1+K1es1t,又可以对系数 K1 进行近似
K1=s1−s2s2=−2ζ2−1ζ+ζ2−1≈−2ζζ+ζ=−1
所以系统的时域响应最终可以近似为
c(t)=1−es1t=1−e(−ζ+ζ2−1)ωnt,t≥0
不难发现,这时系统的响应就类似于一阶系统的响应。
-
从复频域来看,我们可以对闭环传递函数进行近似
R(s)C(s)=(s−s1)(s−s2)ωn2=s−s1−s1⋅s−s2−s2=s−s1−s1⋅1−s2s1=s−s1−s1⋅(1+s2s+⋯)≈s−s1−s1
由此,我们可以得到闭环传递函数的近似表示,它具有一阶系统闭环传递函数的形式
R(s)C(s)=s−s1−s1=s+ζωn−ωnζ2−1ζωn−ωnζ2−1
如果计算它的单位阶跃响应,不难发现具有和时域近似类似的形式,这说明我们这样做是合理的。
C(s)=s(s−s1)−s1=s1−s−s11⟶L−1c(t)=1−e(−ζ+ζ2−1)ωnt,t≥0
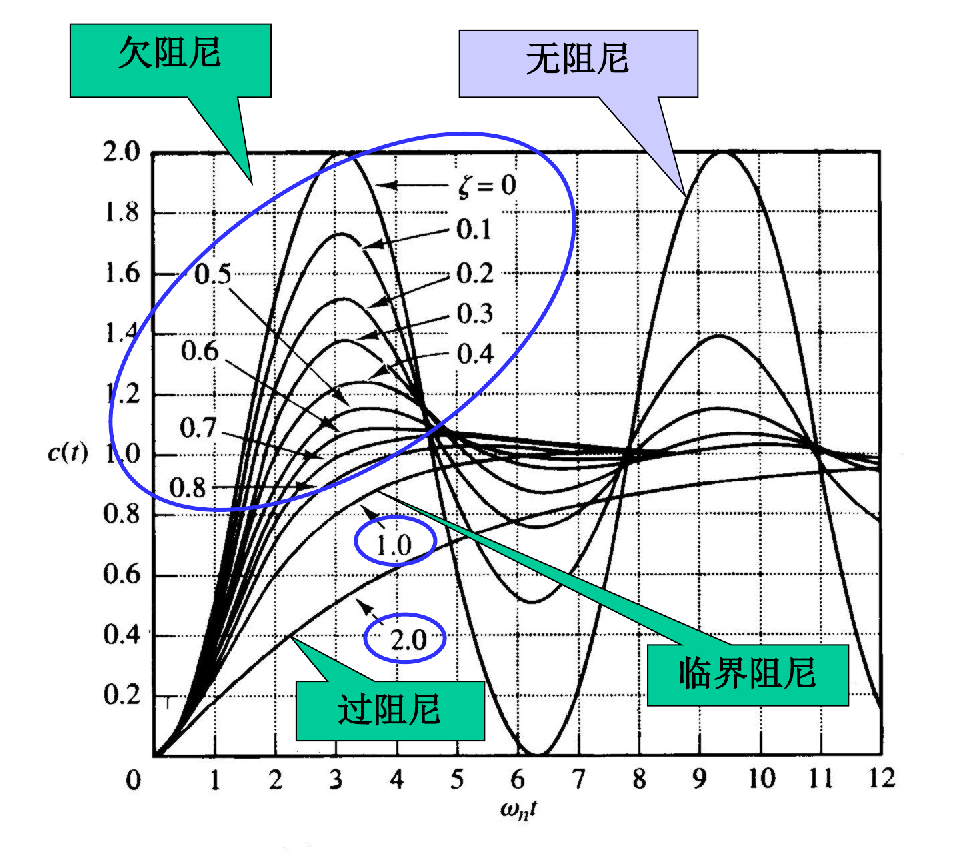
瞬态响应指标的定义 (以及针对欠阻尼二阶系统的计算)
![image-20251009101900085]()
-
延迟时间 td (Delay time): 响应曲线第一次达到稳态值一半所需要的时间。
-
上升时间 tr (Rise time): 响应曲线从稳态值的10%上升到90%(或0%到100%,我们选取0%到100%计算)所需要的时间。
⟹⟹⟹c(tr)=1−1−ζ2e−ζωntrsin(ωdtr+β)=11−ζ2e−ζωntrsin(ωdtr+β)=0sin(ωdtr+β)=0ωdtr+β=kπ(k=0,1,2,⋯)
- 当 k=0 时,ωdtr+β=0⟹tr=−ωdβ。因为 β>0 且 ωd>0,所以这是一个负值,不符合物理意义。
- 当 k=1 时,ωdtr+β=π⟹tr=ωdπ−β。这是第一个使 tr 为正值的解,正是我们要求的上升时间。
故标准二阶系统的上升时间为
tr=ωdπ−β(where β=arccosζ)
-
峰值时间 tp (Peak time): 响应曲线达到过调量的第一个峰值所需要的时间。
在数学上,这是一个极值点,可以通过令导数为零来找到。dtdc(t)=0
求时间响应函数 c(t) 求关于时间 t 的导数:
dtdc(t)=−dtd[e−ζωnt(cos(ωdt)+1−ζ2ζsin(ωdt))]=ζωne−ζωnt(cos(ωdt)+1−ζ2ζsin(ωdt))−e−ζωnt(−ωdsin(ωdt)+1−ζ2ζωdcos(ωdt))=e−ζωnt[(ζωn−1−ζ2ζωd)cos(ωdt)+(1−ζ2ζ2ωn+ωd)sin(ωdt)]
不难发现余弦项的系数为0,从而进一步化简
dtdc(tp)=e−ζωntp(1−ζ2ωn)sin(ωdtp)=0
显然,这个式子中正弦项前面的系数不为0,所以得到
sin(ωdtp)=0⟹ωdtp=kπ(k=0,1,2,…)
- 当 k=0 时,t=0。这是响应的起始点,不是峰值。
- 当 k=1 时,tp=ωdπ。这是导数为零的第一个非零时刻,对应系统响应的第一个极值点,也就是第一个峰值。这就是我们要求的峰值时间。
- 当 k=2 时,t=ωd2π。这对应系统响应的第一个谷值(最小值)。
- 当 k=3 时,tp3=ωd3π。这对应第二个峰值。(这个值后面算衰减比的时候会用到)
故标准二阶系统的峰值时间为
tp=ωdπ=ωn1−ζ2π
-
最大(百分比)过调量 Mp (Maximum overshoot): 响应曲线的最大峰值超出稳态值的量,通常用百分比表示。(也叫超调量)
Mp=c(∞)c(tp)−c(∞)×100%=exp(−1−ζ2ζπ)×100%
-
最大(百分比)过调量的数值直接说明了系统的相对稳定性。过调量越大,系统越不稳定。
-
注意:对于标准二阶系统,Mp 只与阻尼比 ζ 有关。
-
也就是说,欠阻尼二阶系统的相对稳定性只与阻尼比 ζ 有关。ζ(ζ<1) 越大,系统的相对稳定性越好。
- 如果两个二阶系统系统具有相同的阻尼比 ζ 值,但是具有不同的 ωn 值,则两个系统将呈现出相同的过调量和相同的振荡模式,认为二阶系统具有相同的相对稳定性。
-
标准二阶系统最大过调量的计算过程:
Mp=c(tp)−1=−e−ζωnωdπ(cosπ+1−ζ2ζsinπ)=e−ζωnωn1−ζ2π=e−1−ζ2ζπ
-
调整时间 ts (Settling time): 响应曲线达到并永远保持在稳态值的一定误差范围内(通常取稳态值 ±2% 或 ±5% 作为允许误差范围)所需的最短时间。
-
2% 误差标准: ts≈ζωn4=σ4
-
5% 误差标准: ts≈ζωn3=σ3
-
注意:σ=ζωn 正好是极点的实部,在复平面上表征为极点与虚轴的距离
详细计算过程:采用近似方法,不关心振荡的正弦部分,而是直接计算指数衰减包络线本身进入误差带的时间
y(t)=1±1−ζ2e−ζωnt
也就是说,我们要求时间 ts,使得从这时起,暂态响应的幅值(和包络线的位置是对应的)永远小于允许误差。
暂态响应的幅值是 1−ζ2e−ζωnt,为了计算方便(特别是对于0<ζ<0.9,即1−ζ2≈1的情况),工程上常使用指数衰减项 e−ζωnt 来近似代表暂态分量的衰减速度。这正好和一阶系统暂态响应的形式类似,时间常数 T=ζωn1 。
所以,我们求解的是衰减项 e−ζωnt 第一次等于误差限(0.05 或 0.02)的时刻 ts。
对于 ±5% 允许误差限制:
e−ζωnts=0.05⟹−ζωnts=ln0.05≈−2.9957⟹ts=ζωn−ln0.05≈ζωn3=σ3
对于 ±2% 允许误差限制:
e−ζωnts=0.02⟹−ζωnts=ln(0.02)≈−3.912⟹ts=ζωn−ln(0.02)≈ζωn4=σ4
-
衰减比(Decay Ratio) n:同方向的相邻两个波峰(过调量)的比值
n=Mp3Mp=c(tp3)c(tp)=e1−ζ22πζ
-
关于评价指标的说明:我们希望系统的瞬态响应具有以下特性:
- 充分的快速性
- 足够的阻尼
- 阻尼比 0.4<ζ<0.8
- ζ<0.4 瞬态响应严重过调
- ζ>0.8 响应变得过于缓慢
- 最大过调量和上升时间互相矛盾,需要权衡
二阶系统的脉冲响应
1. 二阶系统单位脉冲响应的定义
对于一个二阶系统,当输入为单位脉冲信号 r(t) 时,其在拉普拉斯域的表示为 R(s)=1。此时,系统的输出响应 C(s) 为:
C(s)=s2+2ζωns+ωn2ωn2
通过对该式进行拉普拉斯反变换,就可以得到系统在时域中的单位脉冲响应 c(t)。
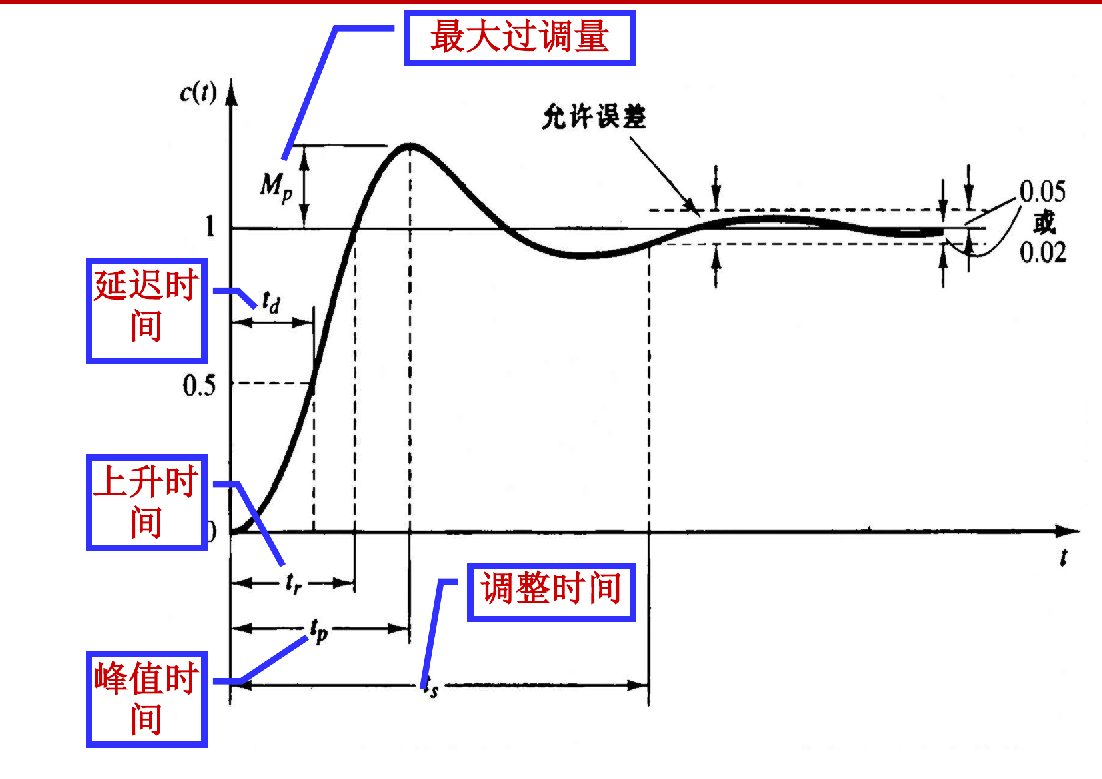
2. 不同阻尼比(ζ)下的时域响应
系统的响应特性由阻尼比 ζ 决定,主要分为三种情况:
- 欠阻尼 (Underdamped): 0≤ζ<1 响应是一个衰减的正弦振荡。其表达式为:
c(t)=1−ζ2ωne−ζωntsin(ωn1−ζ2t),t≥0
- 临界阻尼 (Critically Damped): ζ=1 响应无振荡,始终为正值。其表达式为:
c(t)=ωn2te−ωnt,t≥0
- 过阻尼 (Overdamped): ζ>1 响应同样无振荡,且始终为正值。其表达式为两个衰减指数项的差:
c(t)=2ζ2−1ωne−(ζ−ζ2−1)ωnt−2ζ2−1ωne−(ζ+ζ2−1)ωnt,t≥0
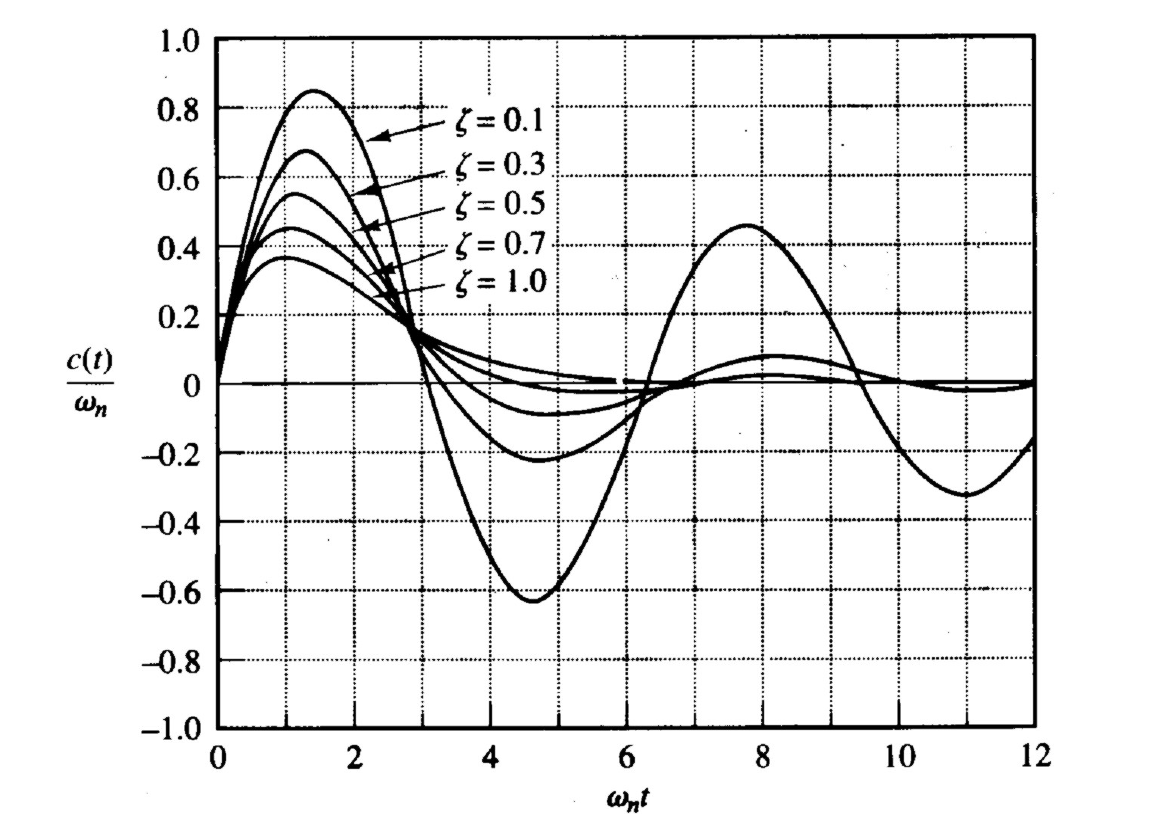
3. 响应曲线特征
![image-20251224115947450]()
从响应曲线图可以看出:
- 欠阻尼 (ζ<1): 响应曲线围绕零值上下振荡,并且阻尼比 ζ 越小,振荡越剧烈,峰值也越大。
- 临界阻尼 (ζ=1) 与过阻尼 (ζ>1): 响应曲线始终大于或等于零,不出现振荡。
- 一个重要结论是:如果一个系统的脉冲响应 c(t) 不改变符号(即没有振荡),那么这个系统必定是临界阻尼或过阻尼的。其对应的阶跃响应将没有超调量,而是单调变化。
4. 欠阻尼系统的最大过调量
对于欠阻尼系统 (0<ζ<1):
t=ωn1−ζ2tan−1ζ1−ζ2
c(t)max=ωnexp(−1−ζ2ζtan−1ζ1−ζ2)
5. 与阶跃响应的关系
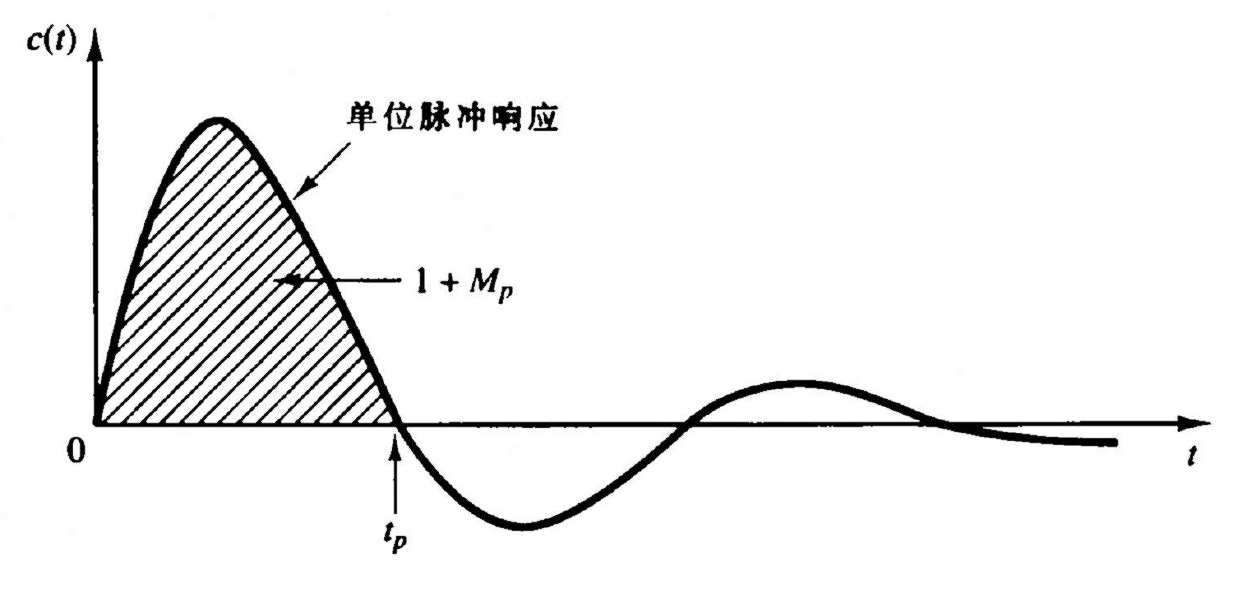
- 单位脉冲响应是单位阶跃响应对时间的导数。因此,单位阶跃响应的最大过调量 Mp 可以通过单位脉冲响应曲线来计算。
- 具体方法是:将单位脉冲响应曲线从 t=0 到曲线第一次与时间轴相交(t=tp)所包围的面积计算出来,这个面积的值就等于 1+Mp。
![image-20251224115921029]()
高阶系统的瞬态响应
高阶系统响应的构成
对于一个高阶闭环系统,其传递函数可以表示为:
R(s)C(s)=(s+p1)(s+p2)⋅⋅⋅(s+pn)K(s+z1)(s+z2)⋅⋅⋅(s+zm)
当输入为单位阶跃信号时,系统的响应 C(t) 在时域上的表现形式,完全取决于其闭环极点 pi 的类型。
- 不相同的实数极点 (pi): 在时域响应中,每个实数极点对应一个指数衰减项 aie−pit。极点 pi 距离虚轴越远(即 ∣pi∣ 越大),其对应的指数项衰减得越快。类似于一阶系统的响应。
- 共轭复数极点 (−ζkωk±jωk1−ζk2): 每一对共轭复数极点对应一个阻尼振荡项。这个振荡的衰减速度由实部 −ζkωk 决定,振荡频率由虚部 ωk1−ζk2 决定。类似于二阶系统的响应。
因此,一个稳定的高阶系统的总响应,是多个指数衰减曲线和阻尼正弦曲线的叠加,也就是说高阶系统的响应可以看作是一系列一阶和二阶系统响应的叠加。对于稳定系统,所有极点都必须位于S平面的左半部分,随着时间趋于无穷,所有这些瞬态项都会衰减至零。
闭环主导极点 (Dominant Closed-Loop Poles)
在众多极点中,并非所有极点都对系统响应有同等重要的影响。那些离虚轴最近且没有被零点抵消的极点,其对应的瞬态分量衰减最慢,从而主导了整个瞬态过程,这些极点被称为闭环主导极点。
判断主导极点的依据如下:
- 位置: 极点离虚轴的距离(即其实部的大小)决定了对应瞬态响应项的指数衰减速率,是关键因素。
- 离虚轴越近的极点,衰减速率越慢。离虚轴最近的极点在瞬态响应中的持续时间是最长的,影响是最大的。简单来说,离虚轴最近的极点起主导作用。
- 如果非主导极点的实部大小是主导极点实部大小的5倍以上(这个定量规则没那么严格),那么由非主导极点产生的瞬态分量会迅速衰减,可以忽略不计。
- 留数: 瞬态响应中每一项的幅值,取决于该极点上的留数(Residue)大小。
- **如果一个极点附近有一个零点,它们的作用会相互抵消,导致该极点上的留数变得很小,从而削弱了它对系统响应的贡献。**因此,即使一个极点离虚轴很近,但如果它旁边有一个零点,它也不是主导极点。
通过忽略那些远离虚轴或被零点抵消的非主导极点,就可以用一个二阶或一阶系统来近似模拟高阶系统的动态特性,从而大大简化分析。
稳定性与瞬态性能在S平面上的体现
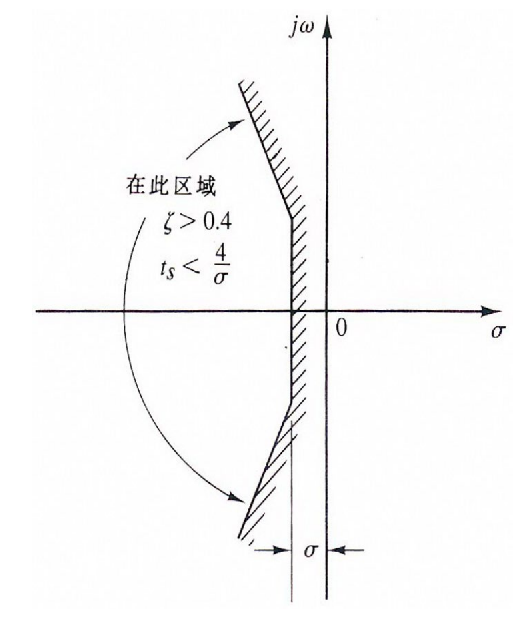
综上所述,为了让高阶系统获得满意的瞬态响应,其主导闭环极点必须位于S平面左半边的一个特定区域内,这个区域同时满足了对响应速度和阻尼的要求。
![image-20251017192306132]()
传统控制论分析高阶系统瞬态响应的基本方法:低阶近似/主导极点近似
-
分析极点位置:首先,分析系统的闭环传递函数,找到其在s复数平面上的所有极点。极点的位置决定了系统响应的模式(指数衰减、阻尼振荡等)和稳定性。
-
寻找闭环主导极点:在所有极点中,辨别出主导极点。判断的依据是:
- 距离虚轴最近:主导极点的实部绝对值远小于其他极点的实部绝对值(通常以5倍以上为界)。因为实部决定了瞬态分量的衰减速度,离虚轴近的极点衰减得最慢,因此在响应中占据主导地位。
- 附近没有零点:如果一个极点非常靠近一个零点,它们的作用会相互抵消,导致这个极点对系统响应的贡献(即留数)变得很小,从而不能成为主导极点。
-
构建近似的低阶系统:根据主导极点的形式进行简化。
- 如果主导极点是一个实数极点,则系统可以近似为一个一阶系统。
- 如果主导极点是一对共轭复数极点,则系统可以近似为一个二阶系统。
-
匹配稳态增益/误差常数:在建立近似的低阶系统模型时,必须调整其增益,使其稳态增益(即s=0时的传递函数值)与原始高阶系统完全相同。这一步至关重要,它保证了简化后的系统在阶跃响应下的稳态值(Final Value)与原系统一致。
- 一般来说,也就是分子上的类似稳态增益(或者说类似误差常数)的系数常数 K 需要变为 Kapprox=∏siKorigin ,其中 ∏si 为所有被舍弃掉的非主导极点的乘积。
-
分析近似系统性能:利用成熟的一阶或二阶系统理论,分析这个简化模型的性能指标(如调节时间、超调量、峰值时间等),并将这些指标作为对原始高阶系统性能的评估。
举例
第一步:定义一个高阶系统
假设我们有一个闭环传递函数为 G(s) 的三阶系统:
G(s)=(s+10)(s2+2s+5)50
这是一个三阶系统,因为分母多项式的最高次幂是3。
第二步:分析极点并寻找主导极点
首先,我们需要找到系统的所有闭环极点,即分母多项式的根:
- 一个实数极点来自 (s+10),即 p1=−10。
- 一对共轭复数极点来自 (s2+2s+5),解得 p2,3=−1±j2。
现在,我们来判断哪些是闭环主导极点 (Dominant Closed-Loop Poles)。
根据课件中的原则:
- 比较极点实部:共轭复数极点的实部是 Re(p2,3)=−1。实数极点的实部是 Re(p1)=−10。
- 找最靠近虚轴极点,应用“5倍原则”:远离虚轴的极点 p1 的实部大小 ∣−10∣ 是靠近虚轴的极点 p2,3 实部大小 ∣−1∣ 的10倍。这远大于课件中提到的5倍标准。
- 检查零点:该系统没有闭环零点,因此不存在零点对极点产生抵消作用的情况。
结论:共轭复数极点 p2,3=−1±j2 是系统的主导极点,因为它们比 p1 离虚轴近得多。这意味着由 p1 产生的瞬态分量 (e−10t) 将会非常快地衰减消失,而由 p2,3 产生的阻尼振荡分量 (e−tsin(2t+ϕ)) 衰减得慢得多,从而在整个瞬态响应中占据主导地位。
第三步:建立近似的低阶系统
既然我们确定了主导极点,就可以忽略非主导极点 (s+10),用一个二阶系统来近似原来的三阶系统。
近似系统的传递函数 Gapprox(s) 将只包含主导极点:
Gapprox(s)=s2+2s+5K
这里的增益 K 需要调整,以保证近似系统的稳态值与原系统相同。对于单位阶跃输入,系统的稳态值(直流增益)可以通过令 s=0 得到。
- 原系统的稳态值:G(0)=(0+10)(02+2(0)+5)50=10×550=1
- 近似系统的稳态值需要与之相等:Gapprox(0)=02+2(0)+5K=5K
令 Gapprox(0)=G(0),即 5K=1,解得 K=5。
因此,简化后的二阶系统为:
Gapprox(s)=s2+2s+55
第四步:比较瞬态响应特性
现在我们来分析这个近似的二阶系统,并将其性能指标与原三阶系统进行对比。
将 Gapprox(s) 与标准二阶系统形式 s2+2ζωns+ωn2ωn2 对比:
- 自然频率 ωn2=5⟹ωn=5≈2.236 rad/s
- 阻尼项 2ζωn=2⟹ζ=ωn1=51≈0.447
根据这些参数,我们可以预测系统的瞬态响应指标:
- 调节时间 (ts,按2%误差带):ts≈ζωn4=14=4 秒。
- 峰值时间 (tp):tp=ωdπ=ωn1−ζ2π=2.2361−0.4472π=2π≈1.57 秒。
- 超调量 (Mp):Mp=e1−ζ2−πζ×100%≈20.8%。
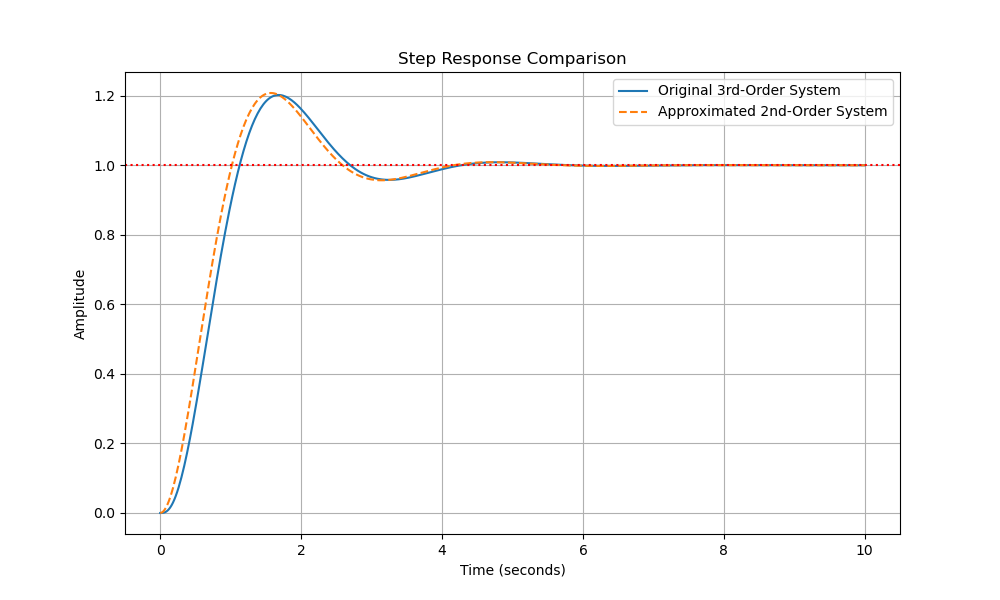
我们可以把这原系统和近似系统的时域中的单位阶跃响应用python画出来,可以看到是非常相似的,这证明我们的近似是合理的。
![]()
劳斯稳定判据 (Routh’s Stability Criterion)
劳斯稳定判据是一种代数方法,可以不求解特征方程的根,直接根据其系数来判断系统的绝对稳定性。
步骤:
-
写出系统的特征方程: a0sn+a1sn−1+⋯+an−1s+an=0
-
必要条件: 系统稳定的一个必要(非充分)条件是所有系数 ai 都必须是正值。
-
构建劳斯阵列:
snsn−1sn−2sn−3sn−4⋮s2s1s0a0a1b1c1d1⋮e1f1g1a2a3b2c2d2⋮e2a4a5b3c3…⋱a6a7…………
其中,
b1c1=a1a1a2−a0a3,b2=a1a1a4−a0a5,b3=a1a1a6−a0a7…=b1b1a3−a1b2,c2=b1b1a5−a1b3,…
-
稳定性判据:
- 稳定条件:系统稳定的充分必要条件是劳斯阵列第一列的所有元素均为正数。
- 不稳定根的数量:劳斯阵列第一列元素符号改变的次数等于特征方程具有正实部根的个数(系统在右半 s 平面极点的个数)。
特殊情况1:第一列某元素为零
对于 第一列某元素为零,但其余各项不等于零或者没有其余项 的情况,可以
- 用一个很小的正数 ε 代替该零,继续计算
- 然后分析当 ε→0+ 时第一列的符号变化:
- 如果位于零(ϵ)上面的系数符号与位于零(ϵ)下面的系数符号相同,表明有一对纯虚根存在,系统可能处于临界稳定状态。
- 如果位于零(ϵ)上面的系数符号与位于零(ϵ)下面的系数符号相反,表明有一个符号变化,存在正实部根,系统是不稳定的。
举例:
![image-20251017202755321]()
![image-20251017202825318]()
特殊情况2:某一行所有元素均为零
某一行所有元素均为零 表明特征方程存在大小相等、方向相反(即在s平面上关于原点对称)的根。这些根可能是:
- 一对或多对纯虚根 (s=±jω)。
- 一对或多对大小相等、符号相反的实根 (s=±σ)。
- 两对或多对共轭复根 (s=±σ±jω)。
解决方法:
- 利用该零行的上一行系数构成辅助多项式 P(s)。
- 用 P(s) 对 s 的导数 dsdP(s) 的系数来替代零行的元素,然后继续完成劳斯表。
辅助多项式有以下特性:
- 辅助多项式一定是一个偶次多项式,也就是说它只包含 s 的偶次幂(例如 s4,s2,s0)。
- 它只可能出现在偶次幂对应的行。由于辅助多项式是全零行的上一行,故全零行只可能是奇数次幂对应的行。
- 辅助多项式的根是原方程根的一部分
构造辅助多项式的方法如下:
- 找到全零行的上一行:在劳斯表中,定位到系数全为零的那一行的正上方一行。
- 利用上一行的系数:将这一行(非零行)的系数,从左到右,作为辅助多项式 A(s) 的系数。
- 确定多项式的幂次:
- A(s) 的最高次幂由该行在劳斯表第一列对应的 s 的幂次决定。
- 后续项的幂次依次递减
2。
举例:
![image-20251017204821560]()
![image-20251017204854167]()
![image-20251017204912797]()
相对稳定性分析
标准的劳斯判据只能判断系统是否绝对稳定(即所有极点是否都在s平面的左半边)。而相对稳定性分析则更进一步,希望知道极点距离虚轴有多远,这通常与系统的动态性能(如调节时间 ts)相关。
分析步骤:
- 坐标轴移动:
- 设定一个实数 σ>0。我们想要判断系统的所有极点是否都在 s=−σ 这条线的左边。
- 为此,进行变量代换,令 s=s^−σ。这个变换相当于将s平面的坐标原点移动到了 (−σ,0) 点,原来的 s=−σ 线变成了新的虚轴 s^=jω。
- 构建新特征方程:
- 将 s=s^−σ 代入系统原来的特征方程,得到一个关于新变量 s^ 的多项式。
- 应用劳斯判据:
- 对这个关于 s^ 的新多项式应用标准的劳斯稳定判据,构建劳斯阵列。
结论判读:
- 劳斯阵列第一列的符号改变次数,等于原系统特征方程在直线 s=−σ 右边的根(即极点)的数目。
- 如果劳斯阵列第一列所有系数均为正(没有符号改变),则说明原系统的所有极点都位于 s=−σ 这条线的左侧。
意义:通过这种方法,我们可以保证系统的所有极点其实部都小于 −σ (即 Re(si)<−σ)。这在工程上意味着可以保证系统的最小衰减率,从而确保系统的响应时间(调节时间 ts)不超过某个预设值(通常 ts≈σ4)。
![image-20251017192306132]()
积分和微分控制作用对系统性能的影响
比例控制 (Proportional Control)
- 作用:按比例反应控制系统的误差信号 e(t)。
- 特点:对于单位阶跃输入,使用纯比例控制且被控系统内无纯积分器的系统(0型系统)会存在稳态误差
- Tips: 不能脱离输入类型和被控系统的类型去讨论一个控制器是否会存在稳定误差
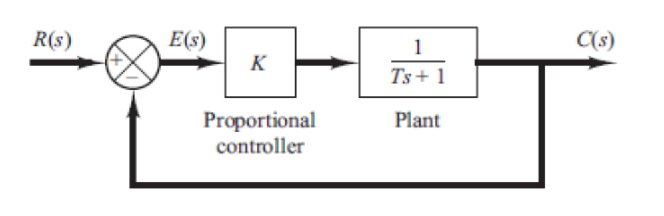
举例计算:使用纯比例控制器控制一个标准一阶系统(一阶延迟积分器),计算单位阶跃输入下的稳态误差
![image-20251224122304229]()
先求系统从参考信号到误差的闭环传递函数 E(s)/R(s)
G(s)=Ts+1K⟹R(s)E(s)=R(s)R(s)−C(s)=1−R(s)C(s)=1+G(s)1=Ts+1+KTs+1
然后求误差信号的表达式 E(s)
E(s)=Ts+1+KTs+1R(s)=Ts+1+KTs+1s1
由于这是个一阶系统,极点都在LHP,它一定是稳定的,故可以使用终值定理计算稳态误差
ess=t→∞lime(t)=s→0limsE(s)=s→0limTs+1+KTs+1=K+11
故稳态误差
ess=1+Kp1
积分控制 (Integral Control)
- 作用:对误差信号进行积分,只要存在误差,积分作用就不断地累积,直到误差消失。
- 特点:对于无纯积分器的被控系统,使用积分控制可以消除阶跃输入的稳态误差。即如果在控制器中包含积分作用,对于阶跃输入,稳态误差可以变为零。
- 缺点:可能会降低系统的相对稳定性,即影响瞬态性能,使响应变慢。(积分控制实际上类似于一个滞后矫正,在后面的章节会提到)
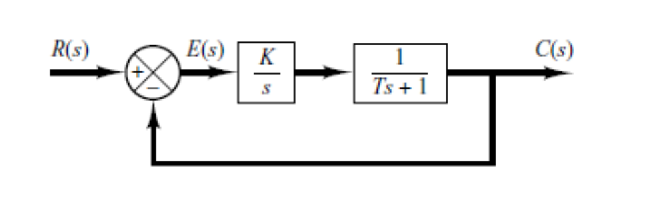
![image-20251224125152874]()
计算举例:一阶系统不变,仍然是单位阶跃输入,控制器换成积分控制,计算稳态误差
R(s)E(s)=R(s)R(s)−C(s)=1+G(s)1=s(Ts+1)+Ks(Ts+1)
二阶系统,显然极点都在LHP,系统稳定,可以使用终值定理
ess=t→∞lime(t)=s→0limsE(s)=s→0limTs2+s+KTs2+s=0
故包含积分作用后,对于阶跃输入,稳态误差可以变为零
微分控制 (Derivative Control)
- 作用:反映误差信号的变化速度(导数),能预测误差的变化趋势,在作用误差的值变得很大之前,产生一个有效的提前修正。
- 特点:
- 优点:能够增加系统的阻尼,主要改善系统的动态性能,提高稳定性。由于加上微分控制后,允许使用更大的比例增益,故(间接)有助于减小稳态误差。
- 缺点:对噪声敏感,且不能单独使用,通常与比例或比例积分控制结合形成 PD 或 PID 控制器。
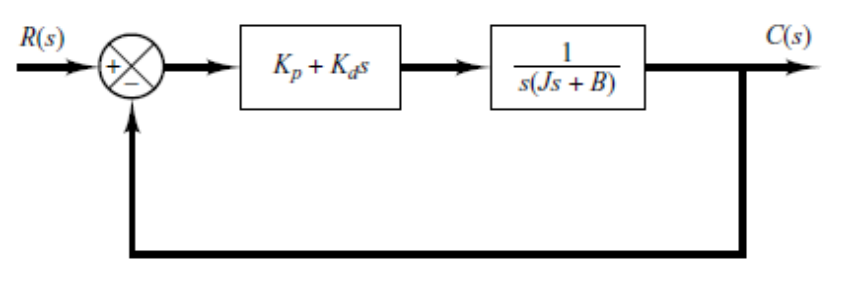
举例:二阶系统的PD控制对斜坡输入的稳态误差
![image-20251224214708720]()
闭环传递函数为
R(s)C(s)=Js2+(B+Kd)s+KpKp+Kds
误差的传递函数
R(s)E(s)=1−R(s)C(s)=Js2+(B+Kd)s+KpJs2+Bs
对于斜坡输入 r(t)=t→LR(s)=s21 ,稳态误差为
ess=t→∞lime(t)=s→0limsE(s)=s→0limsJs2+(B+Kd)s+KpJs2+Bss21=KpB
特征方程为 Js2+(B+Kd)s+Kp=0,易得阻尼比 ζ=2KpJB+Kd
可以看到微分项 Kd 的引入增大了系统的阻尼比
完整的PID控制传递函数
E(s)U(s)=Kp(1+Tis1+Tds)=TisKp(1+Tis+TiTds2)
对扰动的响应分析
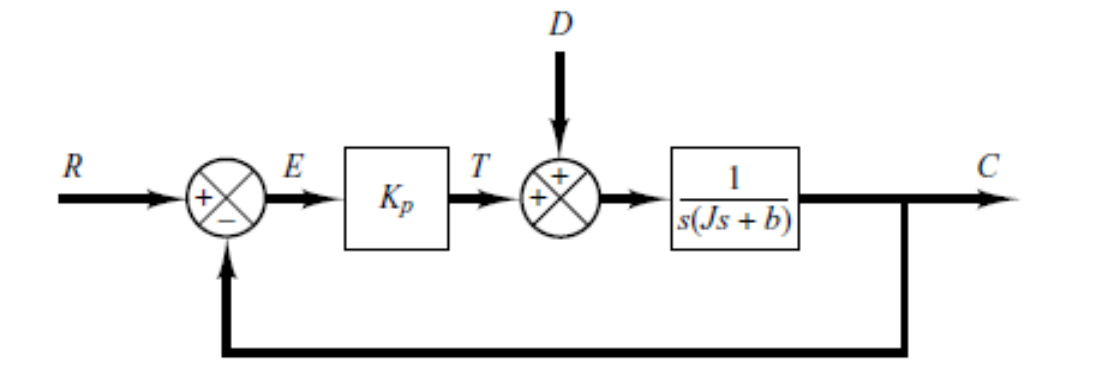
P控制下
![image-20251224210843687]()
用叠加原理,参考输入置零,分析扰动输入到误差信号的传递函数:通过闭环反馈公式得到到输出信号的传递函数,然后就可以得到到误差信号的传递函数
D(s)E(s)=−D(s)C(s)=−1+s(Js+b)Kps(Js+b)1=−Js2+bs+Kp1
这是个二阶系统,极点都在LHP,是稳定的,使用终值定理计算稳态误差
ess=t→∞lime(t)=s→0limsE(s)=s→0lim−sJs2+bs+Kp1s1=−Kp1
稳态误差不为0,可见P控制无法完全消除扰动的影响,系统输出和参考输入会存在一个 −Kp1 的误差。控制器的比例增益 Kp 越大,稳态误差就越小,但无法完全消除。
特征方程 Js2+bs+Kp=0 ,容易计算出阻尼比 ζ=2KpJb 。可见,在被控系统固定的情况下,增加比例增益 Kp ,响应速度会变快,即消除误差的速度会变快,但是相对稳定性可能会变差,即扰动可能会导致震荡,并且在欠阻尼情形下,震荡会变得剧烈。
PI控制下
D(s)E(s)=−D(s)C(s)=−1+s(Js+b)Kp(1+Tis1)s(Js+b)1=−Js3+bs2+Kps+TiKps
假定系统是稳定的,稳态误差为
ess=t→∞lime(t)=s→0limsE(s)=s→0lim−1+s(Js+b)Kp(1+Tis1)s(Js+b)1=s→0lim−Js3+bs2+Kps+TiKps=0
需要注意的是,特征方程:Js3+bs2+Kps+TiKp=0 这是个3阶系统,参数更加复杂(增加了一个可调整的参数),需要根据具体的系数取值才能分析其极点的分布情况。对于2阶以上的系统,有可能存在RHP极点,不一定稳定!
在系统稳定的前提下,稳态误差为0,可见引入的积分作用可以完全消除扰动的影响,系统可以稳定跟踪参考输入。
单位反馈控制系统中的稳态误差 (Steady-State Errors)
稳态误差是衡量系统控制精度的重要指标。它与系统类型和输入信号形式有关。
控制系统的类型
- 控制系统可以按照其对阶跃输入、斜坡输入和抛物线输入等的跟踪能力进行分类。
- 由单独的输入信号引起的稳态误差大小表明了系统的“优良度”。
(在单位反馈控制系统的场景下)系统类型由其开环传递函数 G(s) 在 s=0 处的极点个数 N 决定,即由开环传递函数中包含的(纯)积分环节数目决定。
G(s)=sN(T1s+1)(T2s+1)…K(Tas+1)(Tbs+1)…
- 0 型系统(Type 0): N=0
- 1 型系统 (Type 1): N=1
- 2 型系统 (Type 2): N=2
- ⋯
单位反馈控制系统的稳态误差
闭环传递函数
R(s)C(s)=1+G(s)G(s)
输入到误差的传递函数
R(s)E(s)=1+G(s)1⟹E(s)=1+G(s)R(s)
对于输入信号 R(s),稳态误差为
ess=t→∞lime(t)=s→0limsE(s)=s→0lim1+G(s)sR(s)
静态误差常数
静态位置误差常数 Kp (对应阶跃输入)
Kp=s→0limG(s)=G(0)
- 对于0型系统 Kp=K
- 对于1型或更高型系统 Kp=∞
系统对单位阶跃输入 r(t)=u(t) 的稳态误差
ess=s→0lim1+G(s)sR(s)=s→0lim1+G(s)ss1=1+G(0)1=1+Kp1
故系统对单位阶跃输入的稳态误差可用静态位置误差常数 Kp 表示
ess=1+Kp1
各型系统对单位阶跃输入的稳态误差
ess={1+K10Type 0Type 1 or higher
静态速度误差常数 Kv (对应斜坡输入)
Kv=s→0limsG(s)
- 对于0型系统 Kv=0
- 对于1型系统 Kv=K1
- 对于2型或更高型系统 Kv=∞
系统对单位斜坡输入的稳态误差
ess=s→0lim1+G(s)sR(s)=s→0lims+sG(s)1=s→0limsG(s)1=Kv1
故系统对单位斜坡输入的稳态误差可用静态位置误差常数 Kv 表示
ess=Kv1
各型系统对单位斜坡输入的稳态误差
ess=⎩⎨⎧∞K10Type 0Type 1Type 2 or higher
静态加速度误差常数 Ka (对应抛物线输入):
Ka=s→0lims2G(s)
- 对于0型系统和1型系统 Ka=0
- 对于2型系统 Ka=K1
- 对于3型或更高型系统 Ka=∞
系统对单位抛物线输入的稳态误差
ess=s→0lim1+G(s)sR(s)=s→0lims2+s2G(s)1=s→0lims2G(s)1=Ka1
故系统对单位抛物线输入的稳态误差可用静态位置误差常数 Ka 表示
ess=Ka1
各型系统对单位斜坡输入的稳态误差
ess=⎩⎨⎧∞K10Type 0 or Type 1Type 2Type 3 or higher
各型系统对三种输入的稳态误差总结
| 系统类型 |
阶跃输入 r(t)=1
ess=1+Kp1 |
斜坡输入 r(t)=t
ess=Kv1 |
抛物线输入 r(t)=21t2
ess=Ka1 |
| 0型系统 |
1+K1 |
∞ |
∞ |
| 1型系统 |
0 |
K1 |
∞ |
| 2型系统 |
0 |
0 |
K1 |
结论:
- 要减小或消除稳态误差,可以增加开环增益 K 或 增加系统中的积分环节数量(提高系统类型)。
- 增加积分环节虽然能改善稳态性能,但通常会降低系统的稳定性和动态响应速度,因此需要在设计中进行权衡。