📚 第六章(2) 控制系统设计的根轨迹法
1. 引言
2. 校正装置的类型与结构
2.1 校正结构
根据校正装置 Gc(s) 在系统中的位置,分为:
-
串联校正 (Series Compensation): Gc(s) 位于前向通路,与被控对象 G(s) 串联。
-
并联 (反馈) 校正 (Parallel or Feedback Compensation): Gc(s) 位于一个内部反馈回路中。
2.2 校正装置
课件主要讨论以下几种校正装置:
2.3 设计步骤 (通用)
设计过程通常是迭代的:
-
建立系统数学模型,调整校正装置参数。
-
建造样机并进行开环试验。
-
通过试探法 (trial-and-error) 修改样机,直到满足所有性能指标。
-
重要提示:使用根轨迹法或频率响应法,设计结果不是唯一的。所以这个不太适合作为考试计算题,但是概念还是可以考的,PID控制参数设计也是可以考的。
2.4 初步设计研究:增减开环极点和零点的影响
3. 超前校正 (Lead Compensation)
超前校正装置本质上是一个高通滤波器,提供正相角,用于改善系统的瞬态响应和稳定性。
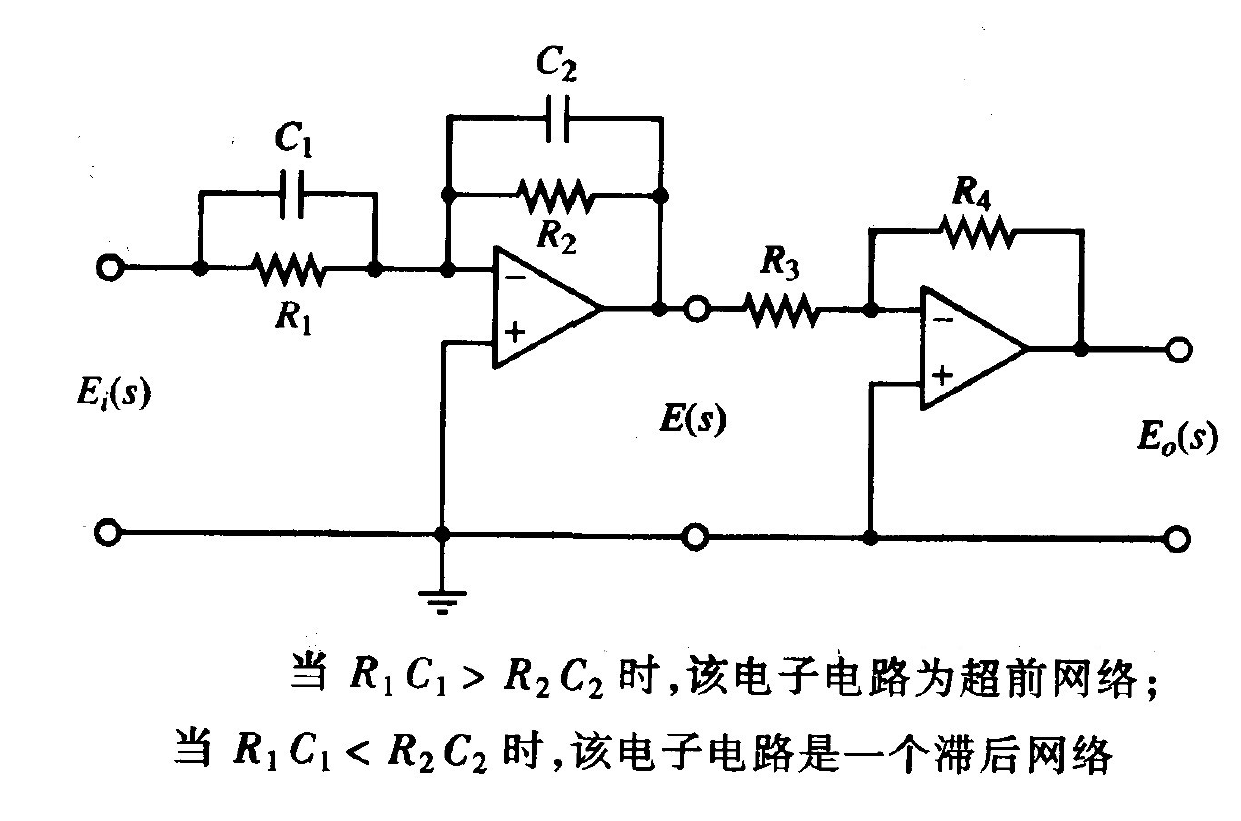
3.1 电子超前网络 (运算放大器实现)
![image-20251226190949931]()
Gc(s)=Ei(s)Eo(s)=KcααTs+1Ts+1=Kcs+αT1s+T1
-
参数定义:
-
T=R1C1
-
αT=R2C2
-
Kc=R3C2R4C1
-
α=R1C1R2C2
-
超前条件:
- 当 R1C1>R2C2 时,即 α<1 (0<α<1),该网络为超前网络。
-
极-零点分布:
3.2 基于根轨迹的超前校正设计步骤
-
确定期望极点:根据性能指标(如 ζ 和 ωn)确定期望的闭环主导极点 sd 的位置。
-
检查原始系统:绘制未校正系统的根轨迹,检查是否能通过调整增益满足要求。
-
计算辐角缺额 (Angle Deficiency):
-
确定 Gc(s) 的极点和零点:
-
即 Gc(sd)=∠(sd+1/T)−∠(sd+1/(αT))=ϕ。
-
有多种方法(如几何法、试探法)来放置这一对零极点以凑出 ϕ 角。
-
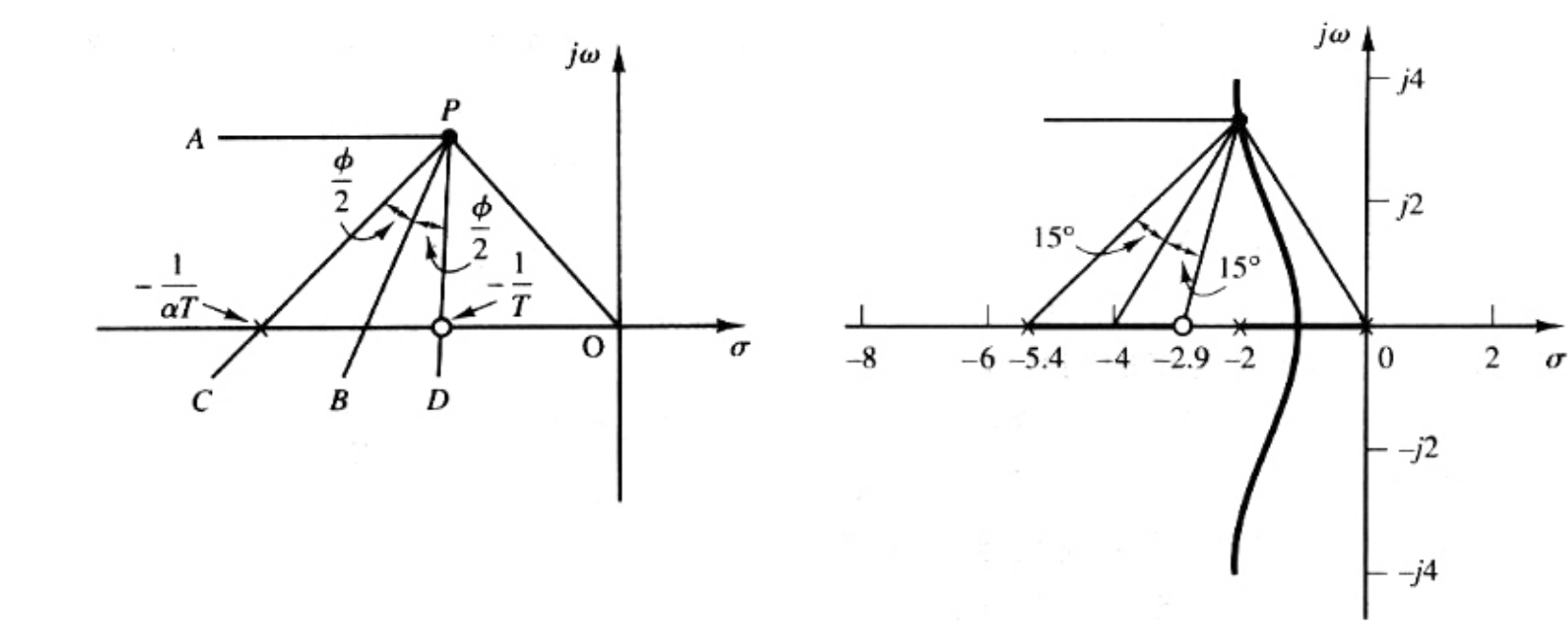
相对最好的一种放置方法是“角平分线法”
- 连接原点与期望极点: 画一条从原点 O 到期望闭环极点 sd 的直线。
- 画水平线: 从 sd 向左画一条水平线。
- 做角平分线: 做出上述两条线夹角的角平分线。
- 对称放置: 以这条角平分线为中心,向两侧各张开 ϕc/2 的角度。这两条边与实轴的交点,就是超前校正装置的零点 zc 和极点 pc。
-
按角平分线法放置,可以得到最大的 α 值(α=pczc)
- 超前校正器在高频段会提升增益,这会放大高频噪声,高频增益的提升倍数正好是 1/α。我们最大化 α,就意味着最小化 1/α,对高频噪声的放大倍数最小,抑制高频噪声。
- 物理实现也更容易: 极点 pc 不需要放置在特别远的位置,这降低了对控制器带宽的要求
- 这种方式能获得最大的静态误差系数 Kp/Kv,从而获得更小的稳态误差 ess,得到相对更好的稳态精度。
-
确定增益:
-
校验:
3.3 超前校正示例
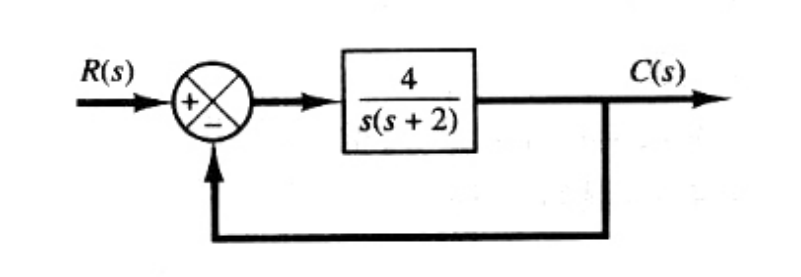
![image-20251226203755933]()
-
系统: 开环传递函数 G(s)=s(s+2)4,闭环传递函数 R(s)C(s)=s2+2s+44
-
原始指标: ζ=0.5, ωn=2 rad/s, Kv=2 s⁻¹
-
设计要求: ζ=0.5, ωn=4 rad/s
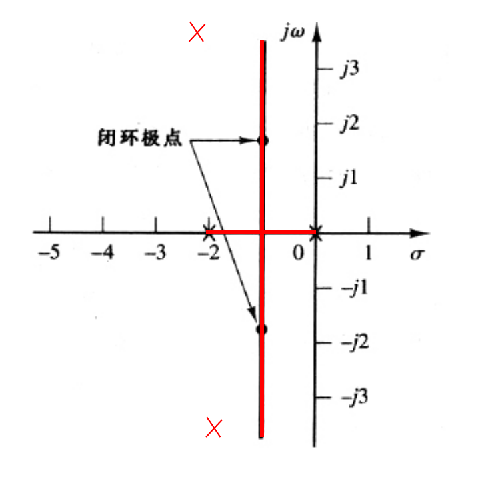
![image-20251226203819160]()
设计过程:
- 期望极点: sd=−ζωn±jωn1−ζ2=−2±j23
- 辐角缺额:
在当前系统的开环极点情况下,期望极点的辐角为
∠G(sd)=∠s(s+2)4∣s=−2+j23=0−∠(−2+j23)−∠(j23)=0−120∘−90∘=−210∘
从而得到辐角缺额 ϕ=180∘−210∘=−30∘ (此处课件记为 ϕ=30∘,表示需要补偿的正相角)
-
放置零极点:课件中选择使用角平分线法
![image-20251226210934573]()
-
确定增益:
-
Gc(s)G(s)=Kcs+5.4s+2.9s(s+2)4=s(s+2)(s+5.4)K(s+2.9)。
-
根据幅值条件 ∣Gc(sd)G(sd)∣=1,解得 K=18.7。
-
由于 K=4Kc,则 Kc=18.7/4=4.68。
-
校正装置为: Gc(s)=4.68s+5.4s+2.9。
-
校验:
-
校正后 Kv=lims→0sGc(s)G(s)=2×5.418.7×2.9=5.02 s⁻¹。 Kv 也得到改善。(但这并非超前校正的本意,只是这个例子恰好稳态性能也提升了)
-
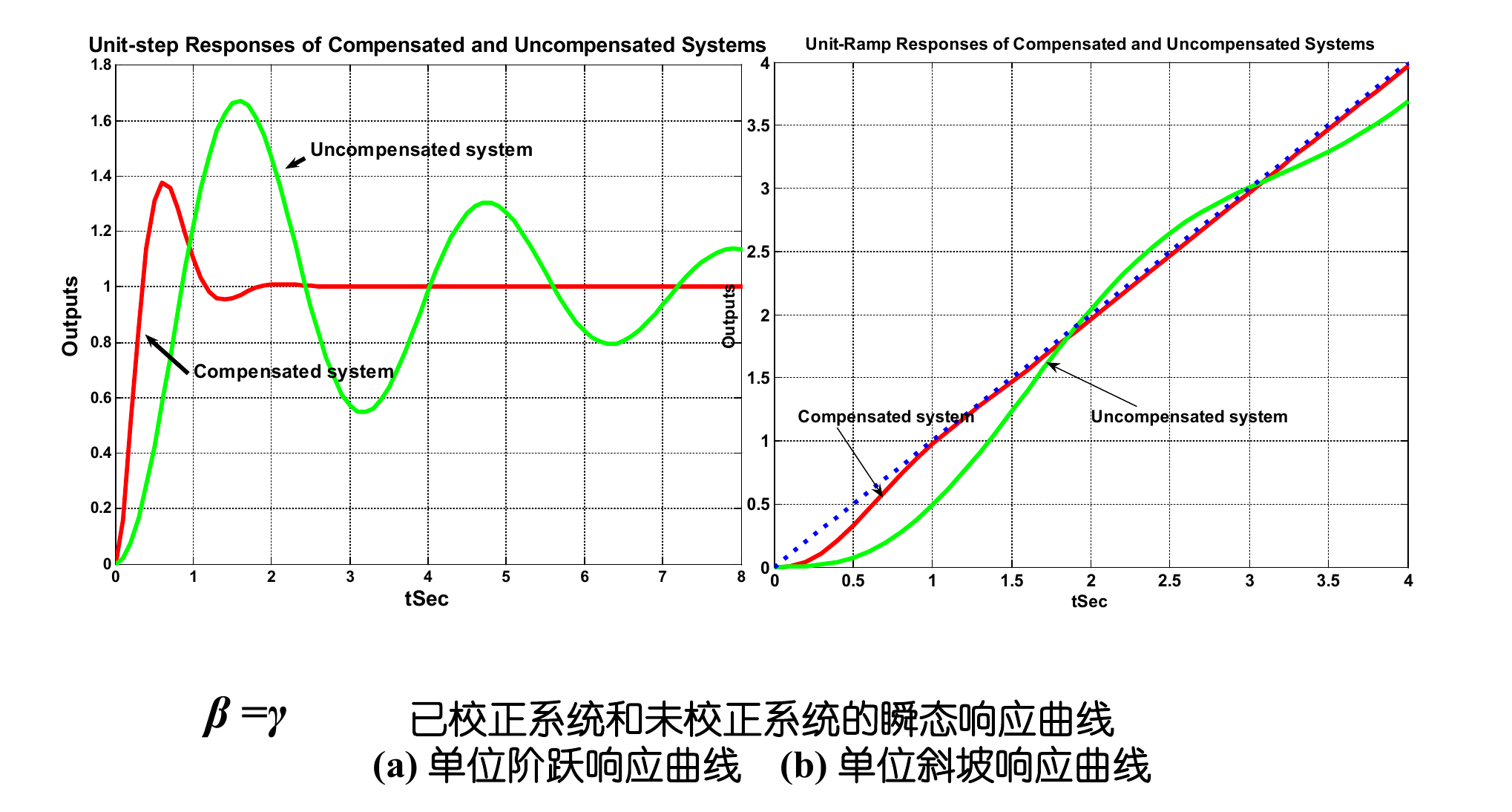
阶跃响应曲线表明,校正后系统(Compensated system)的响应速度明显快于未校正系统(Uncompensated system)。
- 但是,我们也发现,超调量有所增加,但是理论上 ζ 的值在校正前后并没有改变。出现这一现象的原因是,我们引入超前校正使系统阶数升高了(变成3阶),然后在校正计算过程中其实用了主导极点近似,将系统近似为一个二阶系统进行分析。这一近似是存在误差的,虽然近似二阶系统的 ζ 不变,但实际三阶系统的超调量变大了。这其实体现了传统控制方法的局限性,我们只能将主导极点配置到位,其他极点的影响虽然不大,但就是没法控制。
4. 滞后校正 (Lag Compensation)
滞后校正装置本质上是一个低通滤波器,主要用于改善系统的稳态性能(如减小稳态误差),但会牺牲一定的响应速度。
4.1 电子滞后网络
![image-20251226190949931]()
Gc(s)=K^cββTs+1Ts+1=K^cs+βT1s+T1
-
参数定义:
-
T=R1C1, βT=R2C2。
-
K^c=R3C2R4C1。
-
滞后条件:
- 当 R2C2>R1C1 时,即 β>1,该网络为滞后网络。
-
极-零点分布:
4.2 滞后校正的原理
- 适用场景:系统瞬态特性满意,但稳态特性不满意(例如 Kv 太小)。
- 核心思想:
- 不改变瞬态:为不影响原有的瞬态响应(即不改变主导极点 sd 的位置),滞后网络的极点和零点必须靠得非常近,并且都非常靠近S平面的原点。这样,在 sd 处(离原点较远),来自滞后网络的零极点的相角贡献 ≈0∘,且幅值贡献 ≈1。
- 改善稳态:稳态误差常数 Kv 是在 s→0 时计算的。
从稳态误差常数计算的方面进行理解:
- 未校正: Kv=lims→0sG(s)
- 校正后: K^v=lims→0sGc(s)G(s)=lims→0s(K^cs+1/(βT)s+1/T)G(s)
K^v=K^c(1/(βT)1/T)s→0limsG(s)=K^cβKv
-
设计取舍:通常设置 K^c≈1,这样校正后的 K^v≈βKv。
-
结论:滞后校正通过在原点附近设置一个(极点/零点)比值为 1/β 的零极点对,将稳态速度误差常数提高了 β 倍,而几乎不影响瞬态响应的主导极点。
-
副作用:滞后校正引入了一个靠近原点的“慢”闭环极点,这会导致响应中出现一个幅值很小、但衰减很慢的拖尾现象,从而增大了系统的调整时间。
4.3 滞后校正设计步骤
-
分析原系统:绘制 G(s) 的根轨迹,根据瞬态指标确定满意的主导闭环极点 sd 及其对应的增益 Korig。
-
计算 Kv:计算原系统的 Kv,orig。
-
确定 β:根据要求的 K^v,计算 β≈K^v/Kv,orig。
-
放置零极点:
-
确定增益:
-
校正后 Gc(s)G(s)=(K^cs+1/(βT)s+1/T)G(s)。
-
新的根轨迹与原轨迹在 sd 附近几乎重合。
-
在 sd 处, ∣Gc(sd)∣≈K^c。为保持 sd 位置不变,幅值条件要求 ∣Gc(sd)G(sd)∣≈1。
-
由于 ∣G(sd)∣≈1 (假设 Korig 已经包含在 G(s) 中),我们必须设置 K^c≈1。
-
校验:检查新的 Kv 是否达标,并注意瞬态响应变慢的影响。
4.4 滞后校正示例
![image-20251226214435424]()
-
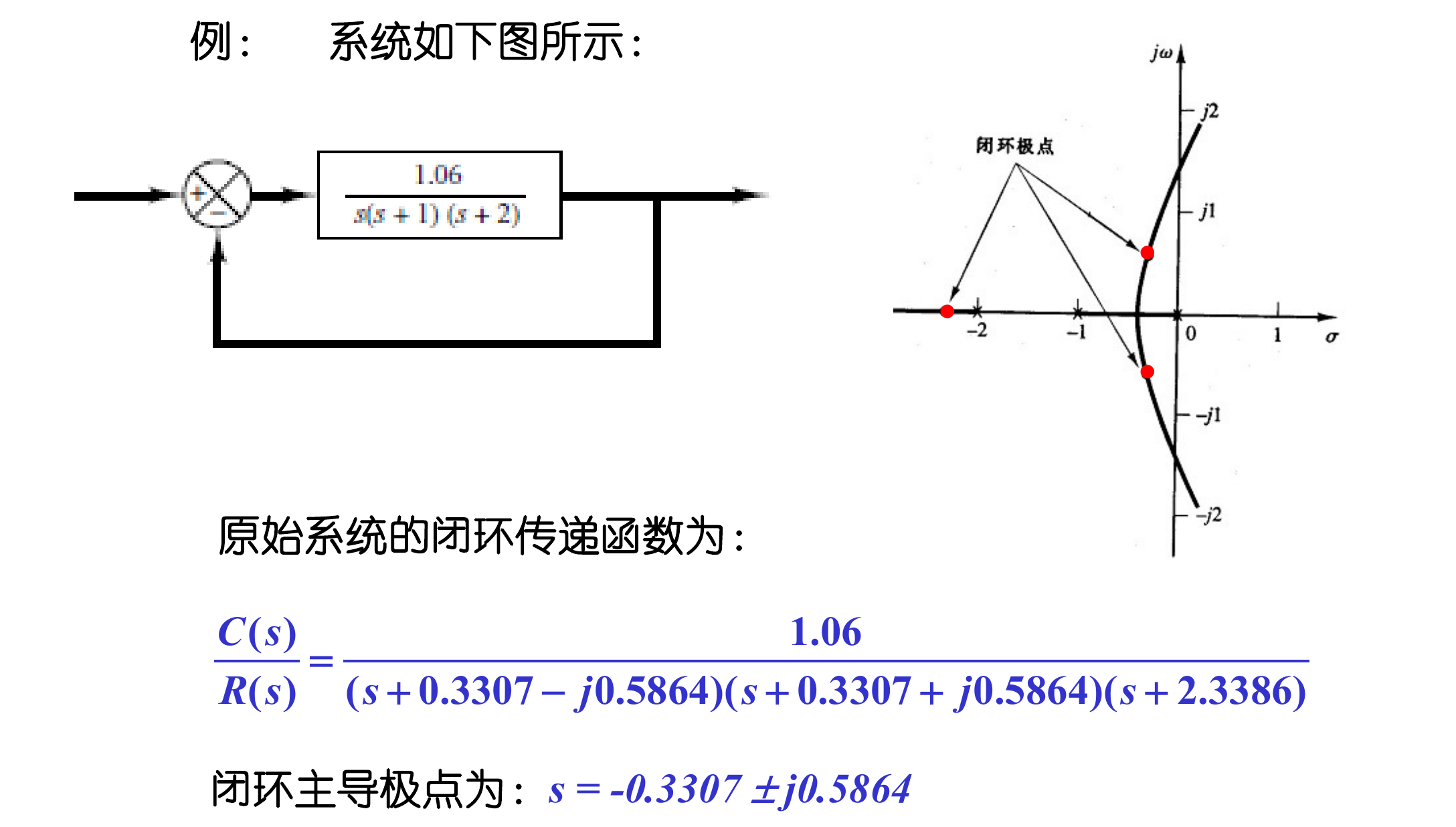
系统: G(s)=s(s+1)(s+2)1.06。
-
原始指标:主导极点 s=−0.3307±j0.5864, Kv=0.53 s⁻¹。
-
设计要求: Kv≈5 s⁻¹,且主导极点位置(瞬态)不变。
设计过程:
-
确定 β: β=K^v/Kv=5/0.53≈9.4。课件中取 β=10。
-
放置零极点:
-
原极点实部为-0.33。选择一个远小于0.33的零点。
-
课件选择 零点: s=−0.05。
-
极点: s=−0.05/10=−0.005。
-
确定增益 K^c:
-
校正后系统 Gc(s)G(s)=s(s+0.005)(s+1)(s+2)K(s+0.05),其中 K=1.06K^c。
-
新的根轨迹上,与原 ζ 对应的新主导极点为 s1=−0.31±j0.55 (与原来非常接近)。
-
在 s1 处用幅值条件: K=∣s+0.05s(s+0.005)(s+1)(s+2)∣∣s1=1.0235。
-
K^c=K/1.06=1.0235/1.06=0.9656 (约等于1,符合预期)。
-
校验:
-
新 Kv=lims→0sGc(s)G(s)=0.005×1×21.0235×0.05=5.12 s⁻¹ (达标)。
-
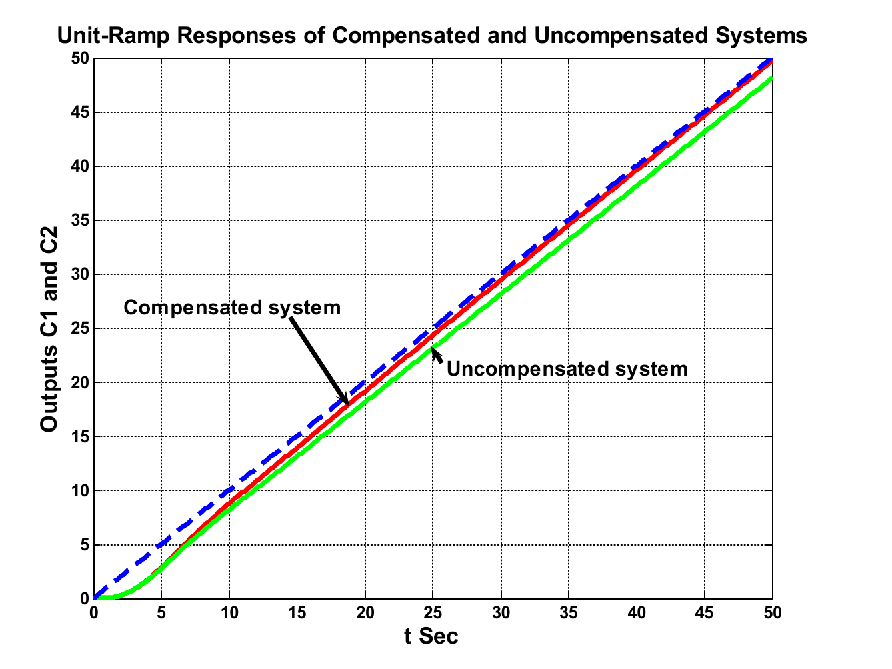
斜坡响应:校正后(Compensated)稳态误差显著减小。
-
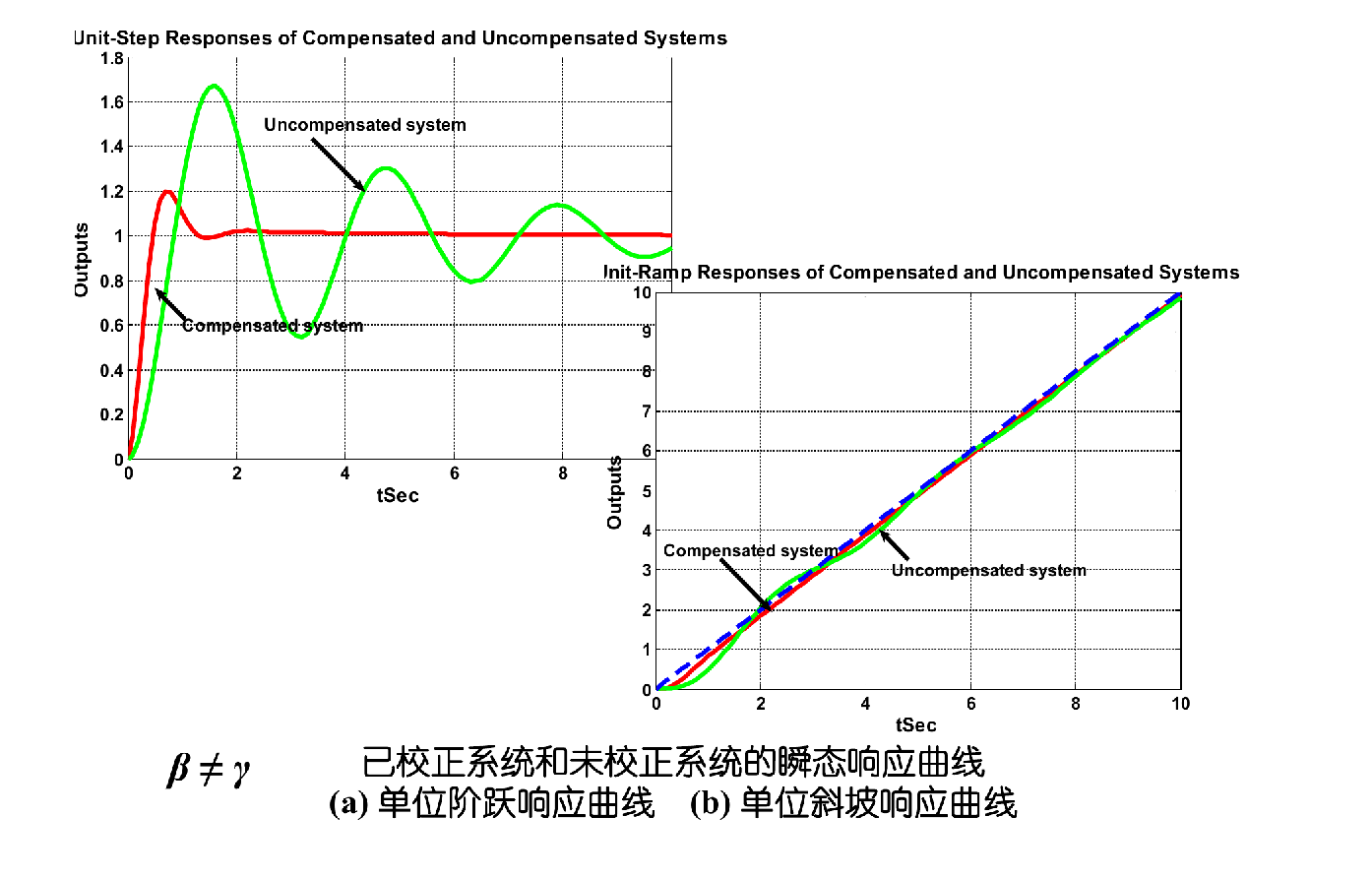
阶跃响应:校正后(Compensated)超调量增大,相对稳定性变差,调整时间变长,系统的响应变得缓慢。损失了一定的瞬态性能,如果单独使用滞后校正,这是难以避免的。如果调整后的瞬态性能不能满足要求的话,那就需要使用滞后-超前校正。
![image-20251226215001089]()
5. 滞后-超前校正 (Lag-Lead Compensation)
综合了超前校正(改善瞬态,相对稳定性增强)和滞后校正(减小稳态误差,改善稳态精度)的优点。
5.1 控制器(校正器)传递函数
Gc(s)=Kc超前部分 (γ>1)(s+T1γs+T11)滞后部分 (β>1)(s+βT21s+T21)
5.2 设计情况一: β=γ
设计过程是先设计超前部分(满足瞬态),再设计滞后部分(满足稳态)。
-
确定期望极点 sd。
-
计算辐角缺额 ϕ。此 ϕ 必须由超前部分提供。
-
设计超前部分:
-
假设滞后部分在 sd 处的幅值为1,相角为0。
-
选择超前部分的零点 s=−1/T1 和极点 s=−γ/T1 来提供 ϕ 角。
-
利用幅值条件 ∣Kc(sd+γ/T1sd+1/T1)G(sd)∣=1 求出 Kc。
-
设计滞后部分:
-
此时 Kc 和 γ 已知。
-
根据速度误差常数 Kv 要求,使用公式 K^v=lims→0sGc(s)G(s)=(Kcγβ)Kv,uncomp 求解 β 。
-
选择 T2:选择一个足够大的 T2,使滞后部分的零点 s=−1/T2 和极点 s=−1/(βT2) 足够靠近原点,以满足步骤3中的假设(即在 sd 处幅值 ≈1,相角 ≈0)。
5.3 示例 (情况一: β=γ)
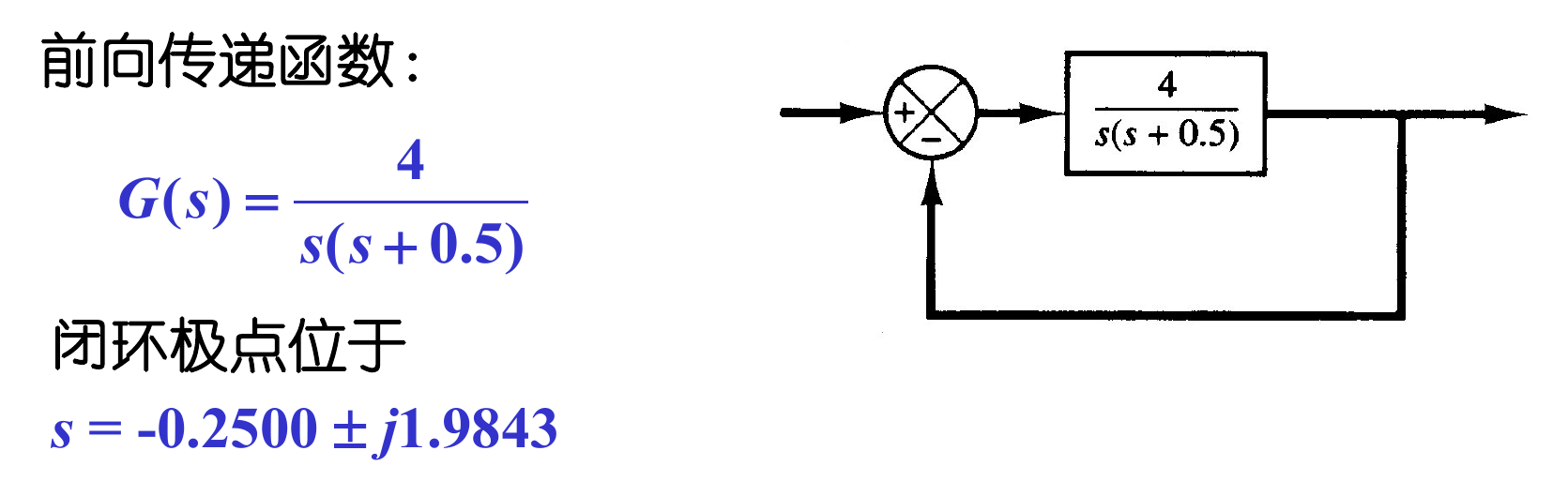
- 系统: G(s)=s(s+0.5)4。
- 原始指标: ζ=0.125, Kv=8。
- 设计要求: ζ=0.5, ωn=5 rad/s, Kv=80 s⁻¹。
设计过程:
![image-20251226221325066]()
-
期望极点: sd=−2.5±j4.33。
-
辐角缺额: ∠G(sd)=−235∘。 ϕ=−180∘−(−235∘)=55∘。
-
设计超前部分:
-
策略:选择超前零点 s=−0.5 来抵消 G(s) 的极点。
-
ϕ=∠(sd+0.5)−∠(sd+γ/T1)=55∘。
-
115∘−∠(sd+γ/T1)=55∘⟹∠(sd+γ/T1)=60∘。
-
解得极点位置 s=−γ/T1=−5.021。
-
⟹T1=1/0.5=2, γ=5.021×T1=10.04。
-
求 Kc: ∣Kcsd+5.021sd+0.5sd(sd+0.5)4∣=∣Kcsd(sd+5.021)4∣=1。
-
解得 Kc=6.26。
-
设计滞后部分:
-
Kv,uncomp=8。
-
Kv=(Kcγβ)Kv,uncomp⟹80=(6.2610.04β)×8。
-
解得 β=16.04。
-
选择 T2:
-
选择 T2=5 (一个足够大的数)。
-
滞后零点 s=−1/T2=−0.2。
-
滞后极点 s=−1/(βT2)=−1/(16.04×5)=−0.01247。
-
校验:
-
最终 Gc(s)=6.26(s+5.02s+0.5)(s+0.01247s+0.2)。
-
校正后系统为三阶(因 s+0.5 被抵消)。
-
新的主导极点 s=−2.4123±j4.2756 ( ζ=0.491,非常接近0.5)。
-
第三个闭环极点 s=−0.2078 被零点 s=−0.2 几乎抵消,影响很小。
-
响应曲线表明,瞬态响应(快速、稳定)和稳态响应(误差小)均满足要求。
![image-20251226224323461]()
5.4 设计情况二: β=γ
减少一个可调整参数,传递函数退化为
Gc(s)=Kc超前部分 (γ>1)(s+T1βs+T11)滞后部分 (β>1)(s+βT21s+T21)
设计步骤顺序相反:先根据稳态要求定 Kc,再设计超前部分。
-
确定期望极点 sd。
-
确定 Kc:
-
在 β=γ 的特殊情况下, Kv=lims→0sGc(s)G(s)=Kc×Kv,uncomp。
-
因此 Kc=Kv,desired/Kv,uncomp。 Kc 由稳态指标直接确定。
-
计算辐角缺额 ϕ。
-
设计超前部分:
-
设计滞后部分:β 已在步骤4中求出。选择一个足够大的 T2 使得滞后部分在 sd 处特性可忽略不计,就完成了设计。
5.5 示例 (情况二: β=γ)
-
期望极点: sd=−2.5±j4.33。
-
确定 Kc:
-
Kv,uncomp=8, Kv,desired=80。
-
Kc=80/8=10。
-
辐角缺额: ϕ=55∘。
-
设计超前部分:
-
需找到零点 z=1/T1 和极点 p=β/T1 满足:
-
∠(sd+z)−∠(sd+p)=55∘。
-
∣10⋅G(sd)∣⋅∣sd+psd+z∣=1⟹∣sd+psd+z∣=∣10⋅G(sd)∣1=40∣sd(sd+0.5)∣=4023.85=0.596 (即 PA/PB=0.596)。
-
通过几何法,解得:
-
β=8.34×T1=8.34×0.42=3.503。
-
设计滞后部分:
-
β=3.503。选择 T2=10。
-
滞后零点 s=−1/T2=−0.1。
-
滞后极点 s=−1/(βT2)=−1/(3.503×10)=−0.0285。
-
校验:
-
最终 Gc(s)=10(s+8.34s+2.38)(s+0.0285s+0.1)。
-
主导极点 s=−2.45±j4.31 (接近期望)。
-
其他极点 s=−0.1003 (被零点 s=−0.1 抵消) 和 s=−3.86。
-
响应曲线同样满足要求,但是可以很明显看出,暂态响应和稳态响应性能都相比方法1略差。这是可以理解的,因为方法2 β=γ 的设定相当于减少了一个可调整的参数。一般情况下,想要兼顾暂态性能和稳态性能,那就需要更多的可调整参数,系统和设计过程都越复杂。而可调整参数很少的情况下,那就很难做到兼顾瞬态与稳态性能,只能有所取舍了。
![image-20251226224242569]()
6. 并联校正 (Parallel Compensation) (不考)
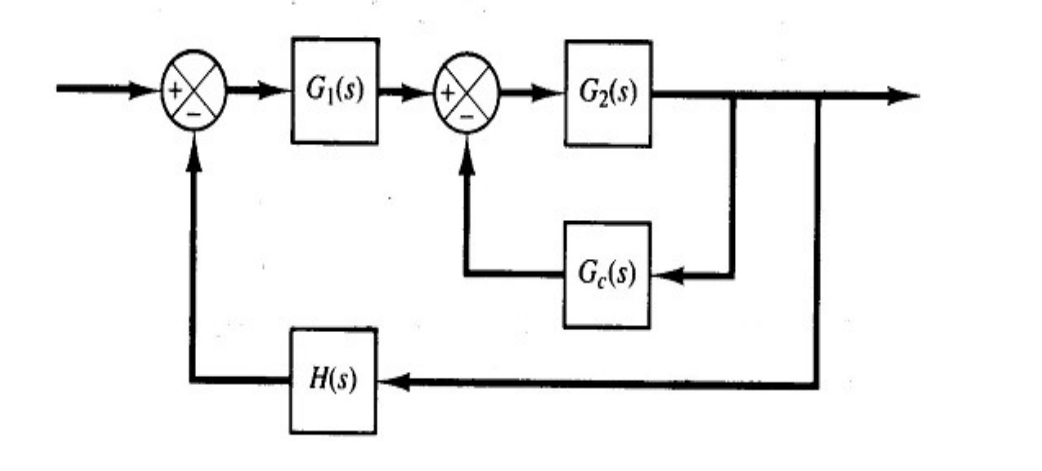
6.1 基本原理
![image-20251226224604286]()
1+1+G1G2HG2Gc=0
Gf=1+G1G2HG2
- 等效:上式 1+GcGf=0。
- 我们现在可以对一个等效的开环传递函数 Gf=1+G1G2HG2 使用根轨迹法来设计 Gc。
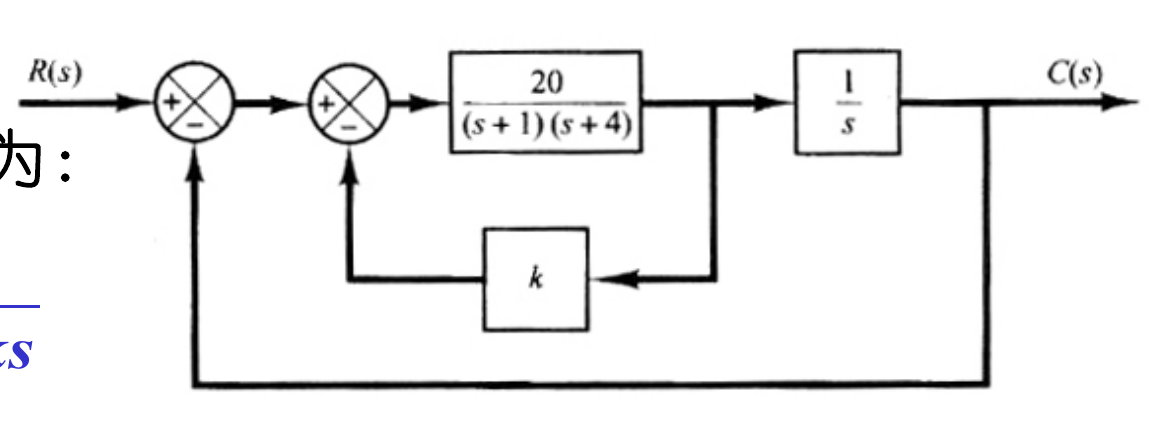
6.2 并联校正示例 (速度反馈)
这个例题挺不错的,考根轨迹,其实和并联校正没太大关系
![image-20251226225251435]()
-
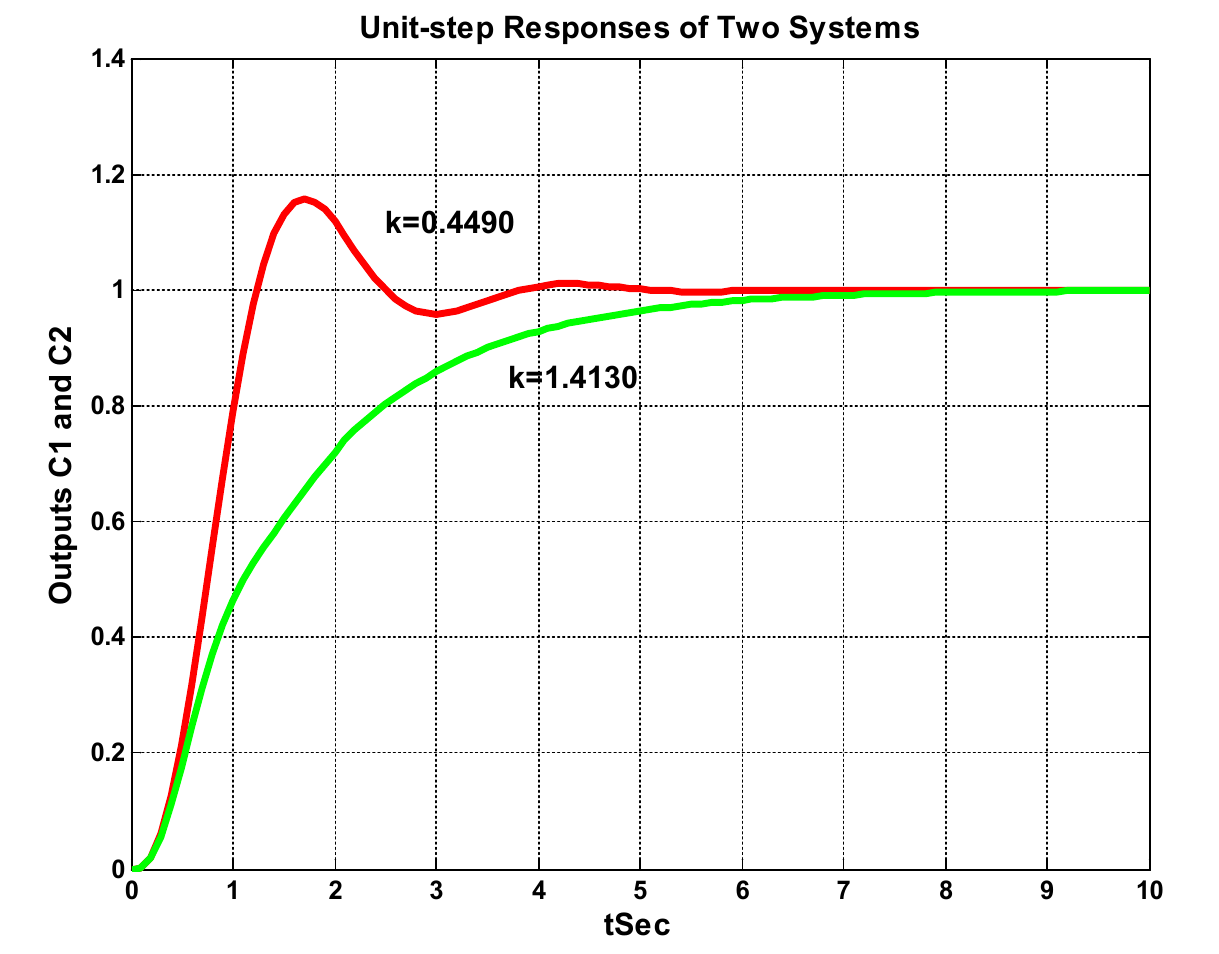
系统:一个带速度反馈(反馈增益 k)的系统。开环传递函数 G(s)=s(s+1)(s+4)+20ks20
-
特征方程: 1+G(s)=0⟹s3+5s2+4s+20ks+20=0
-
变形:(参数 k 是我们要设计的,等效于 Gc)
-
分析等效系统:
-
零点: s=0。
-
极点: s=−5,s=±j2。
-
设计要求:确定 k 值,使闭环主导极点 ζ=0.4。(这个系统应该具有二阶特性)
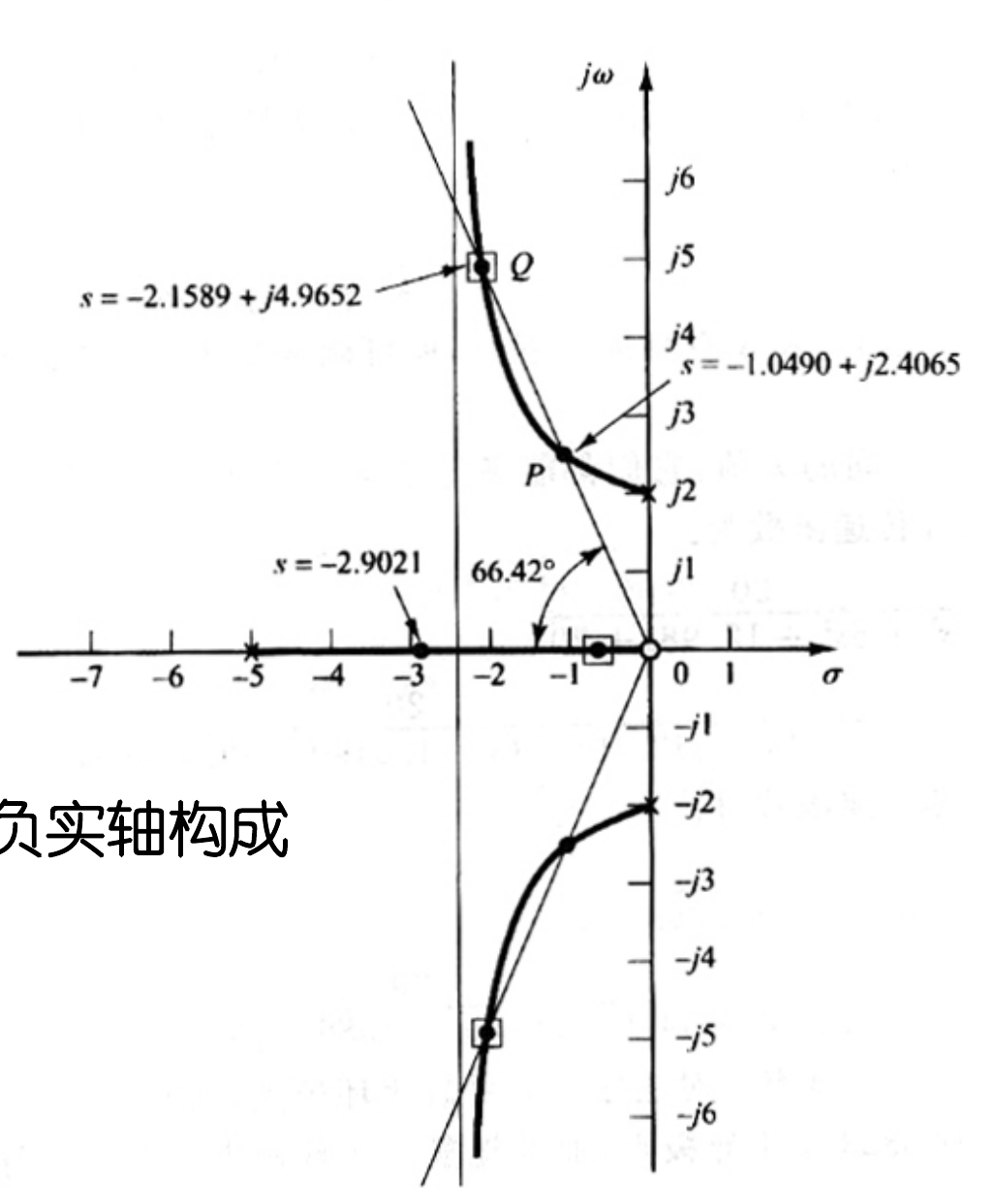
![image-20251226225945519]()
求解:
-
ζ=0.4 对应于从原点出发,与负实轴夹角 θ=arccos(0.4)=66.42∘ 的直线。
-
绘制 Gf 的根轨迹图。
-
ζ=0.4 的直线与根轨迹有两个交点 P 和 Q。
-
交点 P: sP=−1.0490+j2.4065。
-
在 P 点用幅值条件: K=∣1/Gf(sP)∣=∣s(s+5)(s2+4)∣∣sP=8.9801。
-
k=K/20=0.4490。
-
校验:此时闭环极点为 −1.049±j2.4065 和 −2.9021。复数极点是主导极点(实部-1.049 > -2.9021)。
-
交点 Q: sQ=−2.1589+j4.9652。
-
在 Q 点用幅值条件: K=∣1/Gf(sQ)∣=28.260。
-
k=K/20=1.413。
-
校验:此时闭环极点为 −2.159±j4.965 和 −0.6823。实数极点 s=−0.6823 离虚轴更近,它是主导极点。系统表现为一阶特性,不满足 ζ=0.4 的二阶要求。
- 结论:必须选择 k=0.4490。
- 关键:千万别忘了校验等效二阶系统的极点是否是主导极点。如果不是主导极点的话,是不成立的。
![image-20251226230359487]()
7. PID 控制参数的设计 (本章重点)
7.1 P 控制器
Recall: P控制器传递函数
Gc=Kc
- 在原始根轨迹上,根据瞬态和稳态指标选择一个合适的闭环极点位置,该位置对应的 Kc 即为所求。
7.2 PI 控制器
Recall: PI 控制器传递函数
Gc=Kc(1+Tis1)=Kcss+Ti1
7.3 PD 控制器
Recall: PD 控制器传递函数
Gc=Kc(1+Tds)=KcTd(s+Td1)
- 作用:增加一个零点 s=−1/Td。这本质上就是一种超前校正。
- 设计方法:类似超前校正的思路
- 计算期望极点 sd :根据性能指标(如 ζ 和 ωn)确定期望的闭环主导极点 sd 的位置。
- 计算辐角缺额 ϕ,确定PD控制器需要提供的额外辐角。
- 确定微分时间常数 Td ,使得 ∠(sd+Td1)=ϕ
- 根据计算出闭环极点达到期望极点时的静态增益 K=∣G(s)∣∣s+Td1∣1s=sd
- 静态增益 K=KcTd ,反解出比例增益 Kc=TdK
例题(这种形式的题目是有可能考的):系统开环传递函数 G(s)=s(s+2)1。试设计一PD控制器,使系统的动态响应满足: ζ=22, ωn=22
- 期望极点 sd=−2±j2。
- 计算得 G(sd) 的辐角缺额为 ϕ=45∘,PD控制器必须提供 45∘: ∠(sd+1/Td)=45∘。
- 计算 Td:
∠(−2+j2+Td1)=45∘⟹tan(45∘)=Td1−22=1⟹Td1=4⟹Td=0.25
(即 PD 零点放在 s=−4 处)
K=∣G(−2+j2)∣∣−2+j2+4∣1=2222×2=2
Kc=TdK=8
7.4 PID 控制器
Recall: PID 控制器的传递函数
Gc=Kc(1+Tis1+Tds)=KcTisTdTis2+Tis+1
例题:系统开环传递函数 G(s)=s(s+2)1。试设计一PID控制器,使系统的动态响应满足: ζ=22, ωn=22
串联PID可控制器后,系统的开环传递函数变为
G′(s)=G(s)Gc(s)=KcTis2(s+2)(TdTis2+Tis+1)
可见,系统阶数升高1次,变成3阶系统,有3个极点。而我们恰好有3个可配置的参数 Kc Ti Td。所以,我们不仅可以将决定系统暂态性能的两个闭环主导极点配置到我们需要的位置 s1,2=−2±j2 ,还能把另外一个极点也配置到位,也就是3个极点全部配置到位。由于我们希望另一个极点的影响尽可能小,也就是离虚轴尽可能远,我们可以选择一个比如 s3=−10 或者 −20 这样的位置。
这样,我们就可以写出期望的特征方程
(s+2−j2)(s+2+j2)(s+10)=0⟹s3+14s2+48s+80=0
从开环传递函数写出系统的特征方程
G′(s)=−1⟹Kc(TdTis2+Tis+1)+Tis2(s+2)=0
展开,得系统的特征方程
s3+(KcTd+2)s2+Kcs+TiKc=0
比较同幂次系数,使之相等,得到方程组,解方程组得到所有参数的值
⎩⎨⎧KcTd+2=14Kc=48TiKc=80⟹⎩⎨⎧Kc=48Ti=0.6Td=0.25
延伸:
- 这种将系统所有的极点都配置到位的方法,正是后面会讲到的现代控制论中极点配置的内容