Chapter6 Root-Locus Analysis

第六章 根轨迹分析 (Root-Locus Analysis)

本章主要内容包括：

• 引言 (Introduction)
• 根轨迹图 (Root-Locus Plots)
• 根轨迹作图的一般规则 (General Rules for Plotting Root Loci)
• 控制系统设计的根轨迹法 (Root-Locus Method for Control System Design)，包括超前校正、滞后校正和滞后-超前校正。
• 核心思想：画图、读图、用图。

1. 引言

• 核心概念：闭环系统瞬态响应的基本特征与闭环极点的位置紧密相关。
• 设计观点：在某些系统中，通过简单地调整增益，就可以将闭环极点移动到所需要的位置。
• 问题：闭环极点是系统特征方程的根，直接求解非常繁琐。
• 解决方法：W.R.伊凡思 (Evans) 提出的根轨迹法 (Root-Locus Method)。
• 根轨迹法定义：一种图解方法，用来表示系统的特征方程的根（闭环极点）与系统中某一个参数（通常是增益 $K$）从0到 $\infty$ 变化时的关系，即在 $s$ 平面上的轨迹。
• 作用：根轨迹图能揭示每一个开环极点或开环零点对闭环极点位置的影响。

2. 根轨迹图 (Root-Locus Plots)

2.1 根轨迹的基本概念

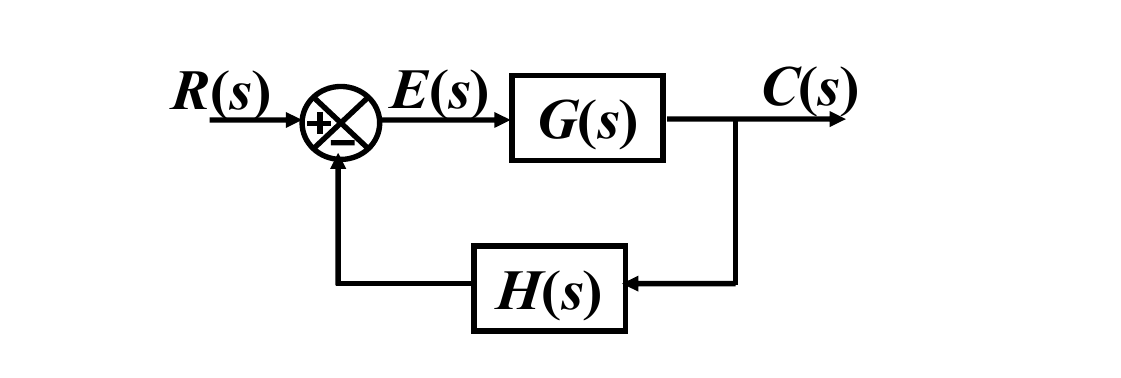
对于一个如图所示的负反馈控制系统：

• 闭环传递函数为： $\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)H(s)}$。
• 特征方程为： $1+G(s)H(s)=0$。
• 根轨迹法的基础是：满足系统的特征方程的根，即系统的闭环极点，就是使开环传递函数 $G(s)H(s) = -1$ 的 $s$ 值。

2.2 根轨迹的两个条件

方程 $G(s)H(s) = -1$ 是一个复数方程，它可以被分解为两个独立的条件：

1. 辐角条件 (Angle Condition)

   $$\angle G(s)H(s)=\pm180^{\circ}(2k+1) \quad k=0,1,2,...$$

   • 定义：复平面上所有满足辐角条件的点的集合，构成了根轨迹。
   • 根轨迹就是 $K = 0 \to \infty$ 时，系统的闭环极点运动留下的轨迹，即 $K \geq 0$ 时对应的所有闭环极点的集合

2. 幅值条件 (Magnitude Condition)

   $$|G(s)H(s)|=1$$

   • 作用：用于确定根轨迹上对应于特定增益 $K$ 值的闭环极点。
   • 同时满足辐角和幅值条件的 $s$ 点，才是系统特征方程的根（即闭环极点）。

2.3 根轨迹条件的图解计算

假设开环传递函数为

$$G(s)H(s)=\frac{K(s+z_{1})}{(s+p_{1})(s+p_{2})(s+p_{3})(s+p_{4})}$$

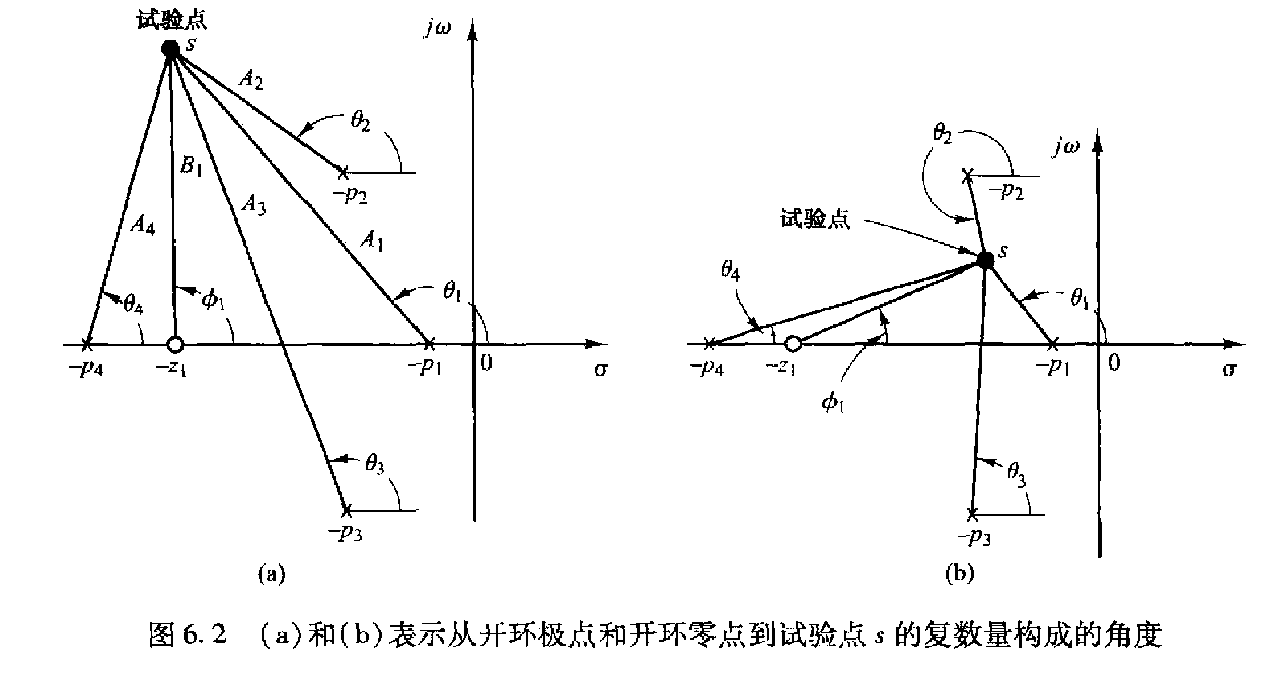
在 $s$ 平面上任取一个试验点 $s$：

• 从每个开环零点（如 $-z_1$）画向量到 $s$ 点，其幅值为 $B_i$，辐角为 $\phi_i$。

• 从每个开环极点（如 $-p_1$）画向量到 $s$ 点，其幅值为 $A_i$，辐角为 $\theta_i$。

1. 图解辐角条件： $s$ 点在根轨迹上，当且仅当该等式成立。

   $$\angle G(s)H(s) = \sum_i \phi_i - \sum_i \theta_i = (\text{所有零点向量的相角和}) - (\text{所有极点向量的相角和})$$

   $$\phi_{1}-(\theta_{1}+\theta_{2}+\theta_{3}+\theta_{4}) = \pm180^{\circ}(2k+1)$$

2. 图解幅值条件：

   $$|G(s)H(s)| = \frac{K \cdot (\text{所有零点向量的幅值乘积})}{(\text{所有极点向量的幅值乘积})} = 1$$

   $$\frac{KB_{1}}{A_{1}A_{2}A_{3}A_{4}} = 1$$

   • 增益 $K$ 的计算：

     $$K = \frac{A_{1}A_{2}A_{3}A_{4}}{B_{1}} = \frac{\prod_i |s-p_i|}{\prod_i |s-z_i|} = \frac{\prod \text{s点到各开环极点的距离}}{\prod \text{s点到各开环零点的距离}}$$

3. 根轨迹作图的一般规则

绘制根轨迹的目的是画出当增益 $K$ 从 $0 \to \infty$ 时，闭环极点的轨迹。

标准形式：

$$1+G(s)H(s) = 1+\frac{K(s-z_{1})(s-z_{2})\cdot\cdot\cdot(s-z_{m})}{(s-p_{1})(s-p_{2})\cdot\cdot\cdot(s-p_{n})}=0$$

---

规则1：起点、终点和分支数

• 起点 ($K=0$)：根轨迹的分支起始于开环极点 $p_i$。
  • 原理：当 $K=0$ 时，幅值条件 $K = \frac{\prod |s-p_i|}{\prod |s-z_i|}$ 要求分子 $\prod |s-p_i| = 0$，因此 $s$ 必须等于某个 $p_i$。
• 终点 ($K \to \infty$)：根轨迹的分支终止于开环零点 $z_i$ （包括有限零点和位于无穷远的零点）。
  • 原理：当 $K \to \infty$ 时，幅值条件要求分母 $\prod |s-z_i| = 0$，因此 $s$ 必须等于某个 $z_i$ 或者 $s \to \infty$。
• 分支数：根轨迹的分支数等于特征方程的阶数，即等于开环极点的数目 $n$。
• 无穷远零点：通常（物理可实现的系统) $n > m$。$m$ 条分支终止于 $m$ 个有限零点，$n-m$ 条分支终止于 $n-m$ 个无穷远零点。

规则2：对称性

• 根轨迹图对称于实轴。
  • 原理：因为特征方程的系数均为实数，其复数根（极点和零点）必须以共轭对的形式出现。

规则3：实轴上的根轨迹

• 判据：实轴上的某一区段是根轨迹的一部分，当且仅当该区段右侧的实数开环极点和实数开环零点的总数之和为奇数。
• 原理简要分析：
  • 复数零极点一定以共轭对的方式，故对实轴上的点 $s$，它们的相角相互抵消，对辐角 $\angle G(s)H(s)$ 的总贡献为0，故对于实数 $s$ ，只需考虑实轴上的
  • 对实轴上的 $s$ ，$s$ 左边的所有点对辐角的贡献为0，$s$ 右边的每一个零点对辐角贡献 $180^{\circ}$ ，每一个极点对辐角贡献 $-180^{\circ}$
  • 故右边零极点总数为奇数个时，总辐角 $\angle G(s)H(s)$ 为 $180^{\circ}$ 的奇数倍

规则4：根轨迹的渐近线 (针对 $n-m$ 条趋于无穷远的分支)

• 渐近线的倾角 $\phi_a$：

  $$\phi_{a}=\frac{\pm(2k+1)180^{\circ}}{n-m}, k=0,1,2,...$$

  • $n$ 是开环极点数，$m$ 是开环零点数。

• 渐近线与实轴的交点 $\sigma_a$：

  $$\sigma_{a}=\frac{\sum_{i=1}^{n}p_{i}-\sum_{i=1}^{m}z_{i}}{n-m}$$

  其中 $\sum p_i$ 是所有开环极点之和， $\sum z_i$ 是所有开环零点之和。

简要推导过程

开环传递函数可以写成如下形式

$$G(s)H(s) = K \frac{B(s)}{A(s)} = -1 \implies \frac{A(s)}{B(s)} = -K$$

将 $A(s)$ 和 $B(s)$ 展开并进行长除法

$$\frac{A(s)}{B(s)} = \frac{s^n - (\sum p_i) s^{n-1} + \dots}{s^m - (\sum z_i) s^{m-1} + \dots} = s^{n-m} + \left( \sum_{i=1}^{m} z_i - \sum_{i=1}^{n} p_i \right) s^{n-m-1} + \dots$$

特征方程近似为

$$s^{n-m} + \left( \sum_{i=1}^{m} z_i - \sum_{i=1}^{n} p_i \right) s^{n-m-1} \approx -K \implies s^{n-m} \left[ 1 + \frac{\sum z_i - \sum p_i}{s} \right] \approx K e^{j(2k+1)\pi}$$

两边开 $(n-m)$ 次方

$$s \left[ 1 + \frac{\sum z_i - \sum p_i}{s} \right]^{\frac{1}{n-m}} \approx K^{\frac{1}{n-m}} \cdot e^{j \frac{(2k+1)\pi}{n-m}}$$

泰勒展开/麦克劳林展开/使用广义二项式定理，并忽略高阶项（只保留一阶项）

$$s \left[ 1 + \frac{1}{n-m} \cdot \frac{\sum z_i - \sum p_i}{s} \right] \approx K^{\frac{1}{n-m}} \cdot e^{j \frac{(2k+1)\pi}{n-m}} \implies s + \frac{\sum z_i - \sum p_i}{n-m} \approx K^{\frac{1}{n-m}} \cdot e^{j \frac{(2k+1)\pi}{n-m}}$$

稍微整理一下

$$s \approx \left( \frac{\sum p_i - \sum z_i}{n-m} \right) + K^{\frac{1}{n-m}} \cdot e^{j \frac{(2k+1)\pi}{n-m}}$$

这个 $s$ 的表达式 $s \approx \sigma_a + R \cdot e^{j \phi_a}$ 恰好完美描述了渐近线的几何形态，其中 $\sigma_a$ 为与实轴的交点， $\phi_a$ 为倾角

规则5：分离点 (Breakaway) 与会合点 (Break-in)

• 定义：根轨迹在实轴上汇合或分离的点（本质上是一个意思），这些点是特征方程的重根。
• 推荐用方法1

计算方法 1： $K$ 对 $s$ 的导数为零。

求解

$$\frac{dK}{ds}=0$$

注意此方法的解需要进行有效性检验： $\frac{dK}{ds}=0$ 的解 $s$ 要是实际的分离点或会合点，还需要满足：

1. 该点 $s$ 必须位于根轨迹上（满足规则3）。
2. 该点 $s$ 对应的增益 $K$ 值必须为正实数 ($K > 0$)。

计算方法 2：

$$\sum_{i=1}^{m}\frac{1}{s-z_{i}}=\sum_{i=1}^{n}\frac{1}{s-p_{i}}$$

分离角/会合角 $\phi_b$

• 若有 $\gamma$ 条根轨迹在一点分离/会合，则它们切线之间的夹角均分 $360^\circ$。

• 与实轴的夹角为：

  $$\phi_{b}=\frac{\pm(2k+1)180^{\circ}}{\gamma}, k = 0,1, \cdots \frac{\gamma - 1}{2}$$

• 最常见的情况（普通分离点）是2条分支在实轴分离，$\gamma=2$，分离角 $\phi_b = \pm 90^\circ$ （即相互垂直）。

  • 在计算上来说，$\frac{dK}{ds} = 0$ 的单根都是普通分离点。即使看上去可能有轨迹交汇，但它们是不同的 $K$ 值时闭环极点经过留下的轨迹。只有取相同的 $K$ 值时，多个闭环极点经过同一点，这一点才会是有大于2条轨迹分离/会合。（下面的高阶分离点情况）

• 特殊的高阶分离点（比较少见，系数要经过特殊设计才会出现）：$\gamma > 2$ ，在计算时表现为 $\frac{dK}{ds} = 0$ 有重根

  • 如果 $\frac{dK}{ds} = 0$ 有 $\gamma - 1$ 重根，则意味着该点有 $\gamma$ 条分支分离/会合
  • $\frac{dK}{ds} = 0$ 二重根，$\gamma = 3$ ，则 $\phi_b = 60^{\circ}$ ，分离点/会合点呈现三叉星图案
  • 再高阶的分离/会合点十分少见，因为系统一般才3阶/4阶，很难有那么多轨迹恰巧在一点分离/会合

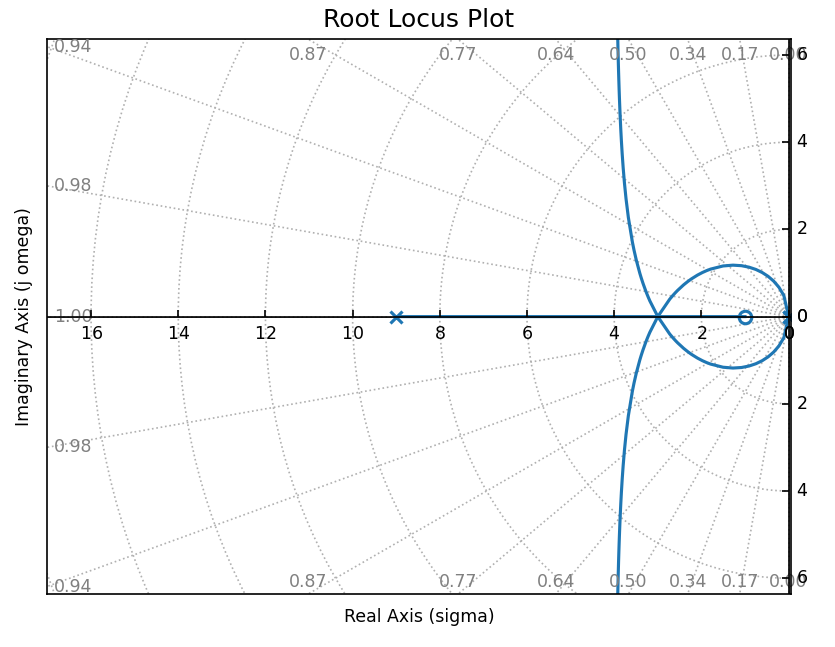
下面这个 $G(s) = \frac{K(s+1)}{s^2(s+9)}$ 是唯一一个在做题过程中遇到的高阶分离点情况

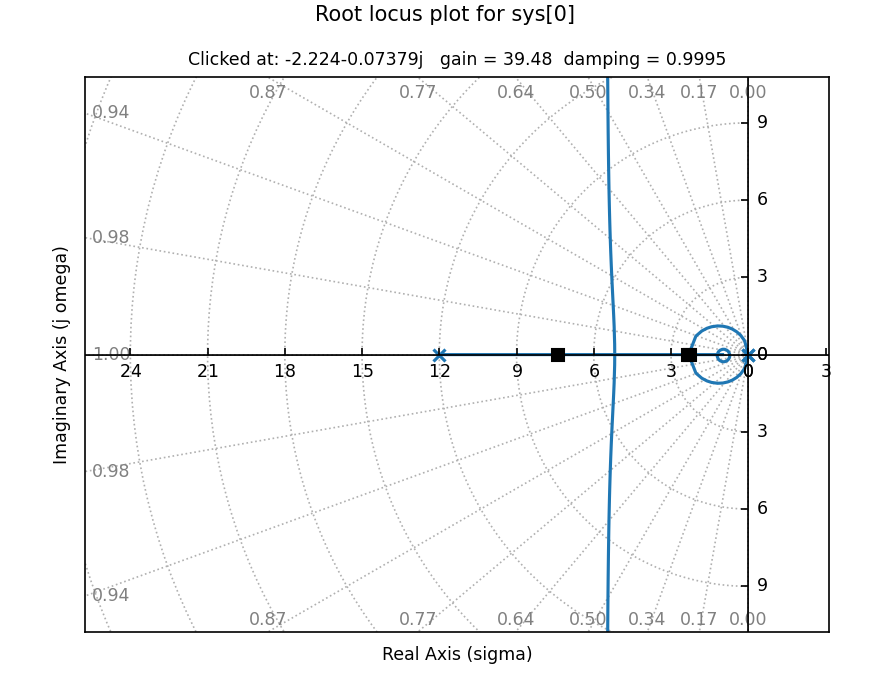
而这是一个看起来有3条轨迹相交，但实际只是普通分离点的情况： $G(s) = \frac{K(s+1)}{s^2(s+12)}$

• 这种情况其实只要算 $\frac{dK}{ds} = 0$ 解出来是单根就可以发现了，不放心的话可以把计算出分离点的K值代进特征方程去看一下另外一个根在什么地方（但其实没必要）。

规则6：与虚轴 $j\omega$ 的交点

• 此点对应系统临界稳定状态。

方法1：劳斯判据 (Routh Criterion)

• 建立特征方程 $s^n + a_{n-1}s^{n-1} + ... + a_1 s + a_0 = 0$ （系数中含 $K$）。
• 构建劳斯阵列。
• 令首列 $s^i$ 行（含$K$）的元素等于0，解出临界增益 $K_{cr}$。
• 利用 $s^{i+1}$ 行（零行之上的行）建立辅助方程（辅助多项式 $= 0$），解出的 $s$ 值即为与虚轴的交点 $s = \pm j\omega$。

方法2：令 $s = j\omega$，解复变方程

• 将 $s = j\omega$ 代入特征方程。
• 分离实部和虚部，令两者分别等于0。

$$(\text{Real Part}) + j (\text{Imaginary Part}) = 0 \implies \begin{cases} (\text{Real Part}) = 0 \\ (\text{Imaginary Part}) = 0 \end{cases}$$

• 联立求解 $\omega$ 和 $K$。

规则7：出射角 (Angle of Departure) 与 入射角 (Angle of Arrival)

• 如果根轨迹从不在实轴上的复数极点出发，或进入
• 出射角：根轨迹离开开环复数极点 $p_j$ 处的切线与实轴的夹角。

$$\begin{aligned} \sum \angle(p_{j}-z_{i}) - \angle\phi_{p,j} - \sum_{i \neq j} \angle(p_{j}-p_{i}) = \pm(2k+1)180^{\circ} \\ \implies \angle\phi_{p,j} = \pm(2k+1)180^{\circ} + \sum \angle(p_{j}-z_{i}) - \sum_{i \neq j} \angle(p_{j}-p_{i}) \end{aligned}$$

• 入射角：根轨迹进入开环复数零点 $z_j$ 处的切线与实轴的夹角。

$$\sum_{i \neq j} \angle(z_{j}-z_{i}) - \angle\phi_{z,j} - \sum \angle(z_{j}-p_{i}) = \angle\phi_{z,j} \\ \implies \angle\phi_{z,j} = \pm(2k+1)180^{\circ} + \sum \angle(z_{j}-p_{i}) - \sum_{i \neq j} \angle(z_{j}-z_{i})$$

规则8：确定闭环极点

• 根轨迹（满足辐角条件）画好后，若要查找特定性能（如阻尼比 $\zeta$）的闭环极点：

  • 例如， $\zeta = \cos(\beta)$，从原点画一条与负实轴夹角为 $\beta$ 的直线。
  • 该直线与根轨迹的交点 $s_d$ 即为所求的主导极点。

• 反求增益K：

  • 确定了交点 $s_d$ 后，利用幅值条件即可求 $K$。

$$K = \frac{\prod |s-p_i|}{\prod |s-z_i|} = \frac{\prod \text{s点到各开环极点的距离}}{\prod \text{s点到各开环零点的距离}}$$

规则9：根轨迹方程推导方法

令 $s = \sigma + j \omega$，代入特征方程 $G(s)H(s) = -1$ ，求解复变方程，整理成 $f(\sigma, \omega) = 0$ 的形式，即为根轨迹方程

$$G(s;K)H(s)|_{s = \sigma + j \omega} + 1 = 0 \implies u(\sigma, \omega; K) + j v(\sigma, \omega; K) = 0 \implies \begin{cases} u(\sigma, \omega; K) = 0 \\ v(\sigma, \omega; K) = 0 \end{cases}$$

想办法消去K，即得根轨迹方程

$$f(\sigma, \omega) = 0$$

二阶开环传递函数的根轨迹很可能有圆、椭圆等二次曲线的形状。更高阶的往往就是一些没什么规律的高次曲线。

扩展方法1：微扰分析

某些情况下，使用已有规则仍然无法明确判断根轨迹在某些关键点的走向，例如从原点出发直接分离的情况下，是直接进入了RHP还是往LHP绕了一圈再进入RHP？

例如这个案例：

$$G(s)H(s) = \frac{K(2s+1)}{s^2(s+2)(s+5)}$$

微扰分析很灵活，大致有这些思路：

1. 进行合理近似：可以忽略那些距离很远的极点和零点在微小运动中造成的辐角变化，但保留距离近的极点和零点带来的影响。这个思路和出射角/入射角的计算类似。
   • 合理近似没有特别统一的哪些影响要保留，哪些可以近似掉的标准，可以灵活进行，但至少要保证能够计算出微扰中闭环极点的运动方向。需要注意的是，一定要保证顺序是优先近似掉距离远的极点，再近似距离近的极点。
   • 例如我们的例子中，可以只保留 $s_{1,2} = 0$ 和 $z_1 = -\frac{1}{2}$
2. 可以使用辐角条件判断：完成近似后，可以用辐角条件判断走向。
   • 例如我们例子中 $\angle (s + \frac{1}{2}) - 2 \angle(s - 0) = - 180^{\circ}$。由于 $\angle (s+\frac{1}{2}) > 0$，必然要有 $\angle (s-0) > 90^{\circ}$ 。也就是说两个极点分离离开原点以后必然先进入LHP绕一圈，之后再往RHP去。
3. 如果已经简化到二阶或以下，直接解近似简化后的根轨迹方程判断，更加清晰准确

$$\frac{K(2s+1)}{10s^2} = -1 \implies 10s^2 + 2Ks + 2K = 0 \implies s_{1,2} = -\frac{K}{10} \pm \frac{j}{10} \sqrt{10K - K^2}$$

显然对于原点附近的微扰，即 $K = \epsilon > 0$ 的时候，闭环极点实部小于0，往LHP运动

---

根轨迹作图基本流程总结

1. 确定开环极点和零点在 s 平面上的位置
2. 确定实轴上的根轨迹
3. 确定根轨迹渐近线
4. 求出分离点与会合点
5. 若有不在实轴上的共轭复数（开环）极点或零点，需要求出每个复数极点的出射角和每个复数零点的入射角
6. 确定根轨迹与虚轴的交点
7. 如果此时根轨迹在某些关键点（例如虚轴交点或者原点）的走向仍然难以判断，需进行微扰分析（进行合理近似，利用辐角条件或复变方程判断）
8. 某些情况下，如有需要，求出根轨迹方程

注意事项

• 手绘根轨迹时，**每一个分支都一定要标出方向！**有些复杂的根轨迹可能需要对每个分支的走向进行文字描述（避免歧义）

【示例1】

$$G(s)H(s) = \frac{K}{s(s+1)(s+2)}$$

• P/Z：$n=3, m=0$。开环极点 $p_1=0, p_2=-1, p_3=-2$。
• 实轴：$(-1, 0)$ 和 $(-\infty, -2)$ 区间。
• 渐近线：$n-m=3$ 条。
  • $\phi_a = \frac{\pm 180^\circ(2k+1)}{3} = \pm 60^\circ, 180^\circ$。
  • $\sigma_a = \frac{(0) + (-1) + (-2)}{3} = -1$ 。
• 分离点：$K = -(s^3+3s^2+2s)$。$\frac{dK}{ds} = -(3s^2+6s+2) = 0$。
  • $s = -0.4226$ ($K=0.3849 > 0$，有效)。
  • $s = -1.5774$ ($K=-0.3849 < 0$，无效)。
• 虚轴交点：特征方程 $s^3+3s^2+2s+K=0$。
  • 劳斯判据：$s^1$ 行为 $\frac{6-K}{3}$。令其为0，得 $K=6$。
  • 辅助方程：$3s^2+K=0 \implies 3s^2+6=0 \implies s = \pm j\sqrt{2}$。
• 设计：求 $\zeta=0.5$ 时的 $K$。
  • $\zeta=0.5$ 对应 $\beta = \cos^{-1}(0.5) = 60^\circ$ 的直线。
  • 交点为 $s = -0.3337 \pm j0.5780$。
  • 用幅值条件求 $K$： $K = |s(s+1)(s+2)|_{s=...} = 1.0383$。
  • 第三个极点：由根之和 $\sum s_i = \sum p_i = -3$，得 $s_3 = -2.3326$。

【示例2】

$$G(s)H(s) = \frac{K(s+2)}{s^2+2s+3}$$

• P/Z：$n=2, m=1$。开环极点 $p_{1,2} = -1 \pm j\sqrt{2}$。开环零点 $z_1 = -2$。
• 实轴：$(-\infty, -2]$ 区间。
• 渐近线：$n-m=1$ 条。
  • $\phi_a = \frac{\pm 180^\circ}{1} = 180^\circ$ （即负实轴）。
• 出射角 (从 $p_1 = -1+j\sqrt{2}$ )：
  • $\theta_1 = 180^\circ + \angle(p_1-z_1) - \angle(p_1-p_2)$
  • $\angle(p_1-z_1) = \angle(1+j\sqrt{2}) \approx 55^\circ$。
  • $\angle(p_1-p_2) = \angle(j2\sqrt{2}) = 90^\circ$。
  • $\theta_1 = 180^\circ + 55^\circ - 90^\circ = 145^\circ$。
  • $p_2$ 的出射角为 $-145^\circ$。
• 会合点：$K = -\frac{s^2+2s+3}{s+2}$。$\frac{dK}{ds} = 0 \implies s^2+4s+1=0$。
  • $s = -0.2680$ （不在实轴轨迹上，无效）。
  • $s = -3.7320$ （在实轴轨迹上，$K=5.4641 > 0$，有效）。
• 会合角：$\gamma=2$ 条分支会合，$\phi_b = \frac{\pm 180^\circ}{2} = \pm 90^\circ$。
• 轨迹：根轨迹呈圆形。

常见情况

• 开环传递函数 $G(s)H(s) = \frac{K}{(s+a)(s+b)}$ 的根轨迹为从两个开环极点开始在实轴上靠近，在中点相遇后沿两个极点的平分线 $\to \infty$

---

4. 特殊情况分析

4.1 根之和特性

• 条件：如果开环传递函数的极点数 $n$ 和零点数 $m$ 满足 $n-m \ge 2$。
• 定理：闭环极点之和是一个常数，恒等于开环极点之和，与增益 $K$ 无关。
  • $\sum_{i=1}^{n} s_i = \sum_{i=1}^{n} p_i = \text{Constant}$
• 推论：当 $K$ 增大时，如果某些闭环极点（根轨迹分支）向左（更稳定）移动，则必有其他分支向右（更不稳定）移动，以保持总和不变。

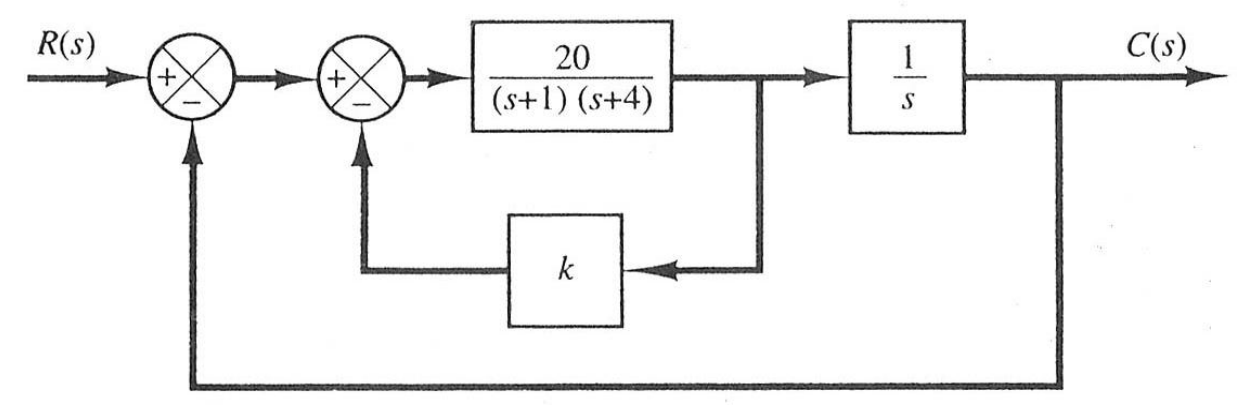
4.2 参数非 $K$ 的根轨迹

开环传递函数

$$G(s)H(s) = \frac{20}{s^3 + 5 s^2 + (4+20k) s}$$

特征方程

$$1 + G(s)H(s) = 0 \implies s^3 + 5s^2 + (4+20k) s + 20 = 0$$

• 问题：当待变参数 $k$ 不在 $G(s)H(s)$ 的分子上时（如上面的例子）。
• 方法：
  1. 写出系统的特征方程。$s^3+5s^2+(4+20k)s+20=0$
  2. 将特征方程代数变形，整理为标准形式 $1 + k' \cdot G'(s)H'(s) = 0$。
  3. 示例：
     • $s^3+5s^2+4s+20 + 20ks = 0$
     • 两边同除以不含 $k$ 的项： $1 + \frac{20ks}{s^3+5s^2+4s+20} = 0$
  4. 此时，可以绘制根轨迹：
     • “等效增益” $K' = 20k$。
     • “等效开环传递函数” $G'(s)H'(s) = \frac{K' s}{s^3+5s^2+4s+20} = \frac{K's}{(s+5)(s^2+4)}$。
  5. 按此 $G'(s)H'(s)$ 的“等效极点”（ $-5, \pm j2$）和“等效零点”（$0$）绘制根轨迹。
  6. 在轨迹上找到所需点（如 $\zeta=0.4$），用幅值条件求出 $K'$，再反解出 $k$。

4.3 开环极点-零点对消

• 问题：当 $G(s)$ 中的一个极点与 $H(s)$ 中的一个零点相同时（如 $G(s)$ 有 $(s+1)$ 因子在分母， $H(s)$ 有 $(s+1)$ 因子在分子）。
• 陷阱：在计算 $G(s)H(s)$ 时，这对极点和零点会相互抵消，使系统的阶数降低。

$$G(s)H(s) = \frac{K(s+1)}{s(s+1)(s+2)} = \frac{K}{s(s+2)}$$

• 后果：基于 $G(s)H(s) = \frac{K}{s(s+2)}$ 绘制的根轨迹，其特征方程为 $s(s+2)+K=0$，这不是完整的系统特征方程。
• 完整特征方程： $\frac{C(s)}{R(s)} = \frac{G}{1+GH} = \frac{K/(s(s+1)(s+2))}{1+K(s+1)/(s(s+1)(s+2))} = \frac{K}{(s+1)[s(s+2)+K]}$。
• 结论：
  1. 完整的特征方程是 $(s+1)[s(s+2)+K] = 0$。
  2. 系统的闭环极点 = { $G(s)H(s)$ 根轨迹上的点 } $\cup$ { $G(s)$ 和 $H(s)$ 之间被消掉的 $G(s)$ 的极点 }。
  3. 在此例中， $s=-1$ 始终是系统的一个闭环极点，无论 $K$ 取何值。

• 通用结论：开环极点-零点对消意味着系统存在一个固定的，不随 $K$ 值改变而移动的闭环极点，表现为根轨迹上有一个始终固定在相消开环零极点处的闭环极点，也可以理解为这个根轨迹分支起始和终止于同一点（相消的开环极点 $\to$ 零点），所以固定不动。这个点在画根轨迹时也需要明确标出，不能漏。

4.4 非最小相位系统

• 最小相位系统：所有开环极点和零点都在 $s$ 左半平面 (LHP)。
• 非最小相位系统：至少有一个开环极点或零点在 $s$ 右半平面 (RHP)。
• 对辐角条件的影响：在计算根轨迹问题，对于非最小相位系统，我们关注的是RHP零点对辐角条件的影响
  • 如果是 $Ts - 1$ 形式的RHP零点，那么辐角条件不变，仍然是 $\angle G(s)H(s) = \pm180^{\circ}(2k+1)$
  • 如果是 $1 - Ts$ 形式的RHP零点，将会引入额外的 $180^{\circ}$ 辐角，辐角条件将会改变为 $\angle G'(s) = \pm 360^{\circ}$ ，根轨迹变成类似正反馈根轨迹（0度根轨迹）的情况。
  • 在根轨迹问题中，**有无RHP零点并不造成实质影响，符号的变化才是重点。**RHP零点多引入了 $-1$ 的系数，才会造成辐角条件改变。当然偶数个个引入 $-1$ 系数的 RHP 零点的作用是会相互抵消的，这个自行灵活判断。
• 示例： $G(s) = \frac{K(1-T_a s)}{s(Ts+1)}$，它在 $s = +1/T_a$ 处有一个 RHP 零点。

$$G(s) = -\frac{K(T_a s-1)}{s(Ts+1)}$$

辐角为

$$\angle G(s) = \angle -\frac{K(T_a s-1)}{s(Ts+1)} = \angle(-1) + \angle\frac{K(T_a s-1)}{s(Ts+1)} = 180^{\circ} + \angle \frac{K(T_a s-1)}{s(Ts+1)}$$

辐角条件变为0度（$360k$ 度）

$$\angle G(s) = \pm180^{\circ}(2k+1) \implies \angle \frac{K(T_a s-1)}{s(Ts+1)} = \pm180^{\circ}(2k) = \pm 360^{\circ} k$$

• 结论：对于开环传递函数中RHP零点有 $1-sT$ 形式的系统，其根轨迹绘制规则等效于 $\angle G'(s) = 0^\circ$ (或 $360^\circ k$)，即正反馈的辐角条件（0度根轨迹）。

4.5 正反馈系统

• 特征方程： $1 - G(s)H(s) = 0$。
• 根轨迹条件： $G(s)H(s) = +1$。
• 辐角条件 (0度根轨迹)： $\angle G(s)H(s) = \pm k \cdot 360^{\circ}$， $k=0,1,2,...$。
• 幅值条件： $|G(s)H(s)| = 1$ （与负反馈相同）。
• 作图规则修改：只有使用了辐角条件的规则需要修改
  1. （规则3）实轴轨迹：实轴上某一区段是根轨迹，当且仅当该区段右侧的实数开环极点和零点总数为偶数（包括0）。
  2. （规则4）渐近线倾角： $\phi_{a}=\frac{\pm k \cdot 360^{\circ}}{n-m}$。
  3. （规则7）出射/入射角：公式中的 $\pm 180^\circ(2k+1)$ 项变为 $\pm k \cdot 360^{\circ}$。
  4. （规则9）算轨迹方程的时候特征方程是 $G(s)H(s) = 1$
  5. 其他规则均不变

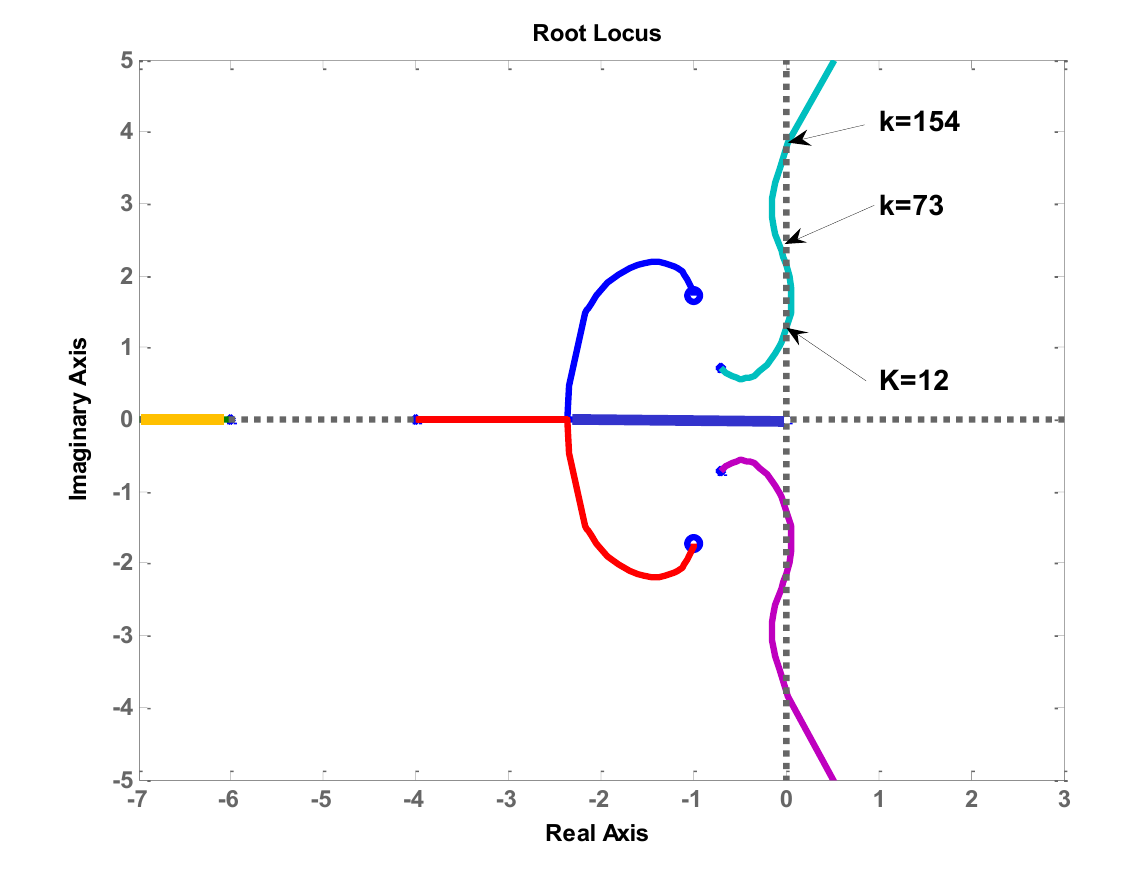
4.6 条件稳定系统

• 定义：系统仅在某几段 $K$ 值范围内稳定，当 $K$ 增大时，系统可能从稳定 $\to$ 不稳定 $\to$ 稳定 $\to$ 不稳定。
• 示例：一个系统的根轨迹可能先进入 RHP，再绕回 LHP，最后又进入 RHP。
• 稳定范围：例如 $0 < K < 12$ （稳定）， $12 < K < 73$ （不稳定）， $73 < K < 154$ （稳定）， $K > 154$ （不稳定）。
• 应用：条件稳定系统在实际中是不能令人满意的。在系统中增加适当的校正网络，可以消除条件稳定性问题。

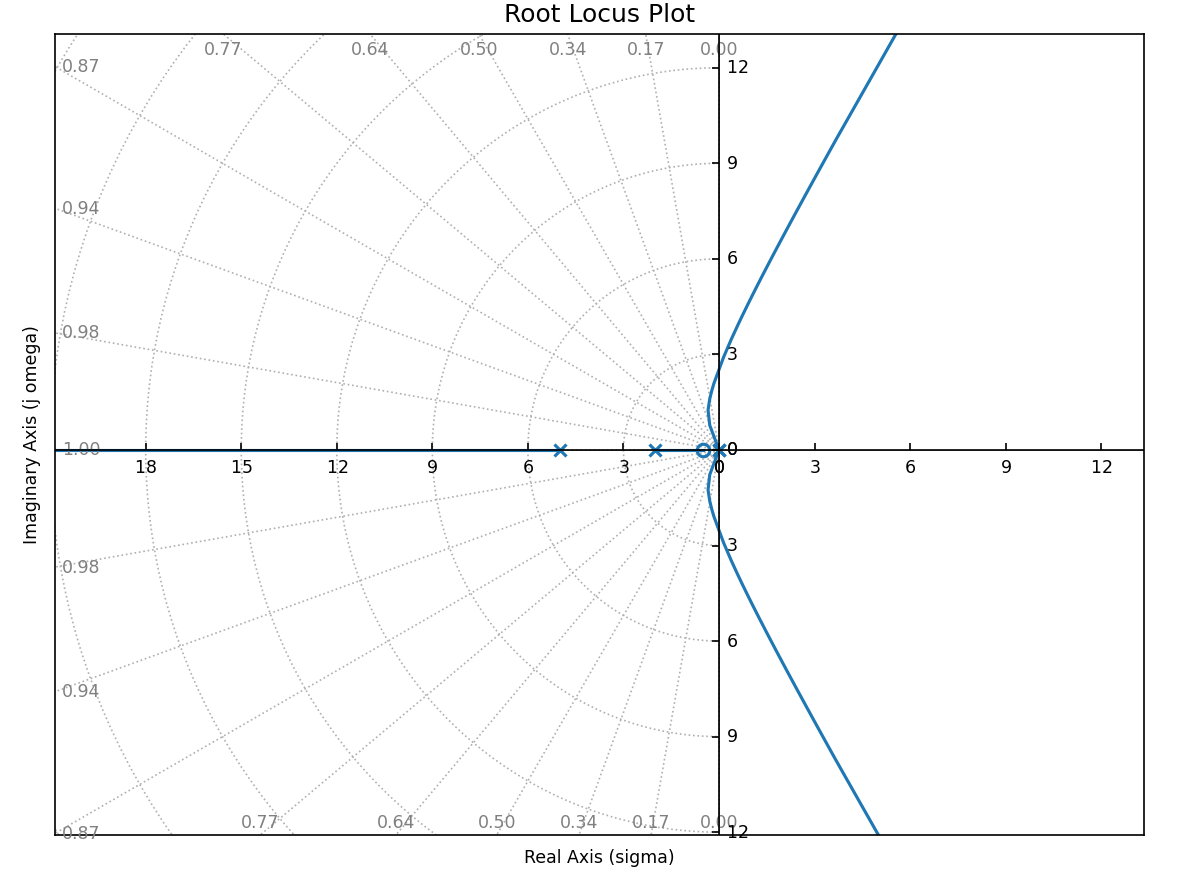
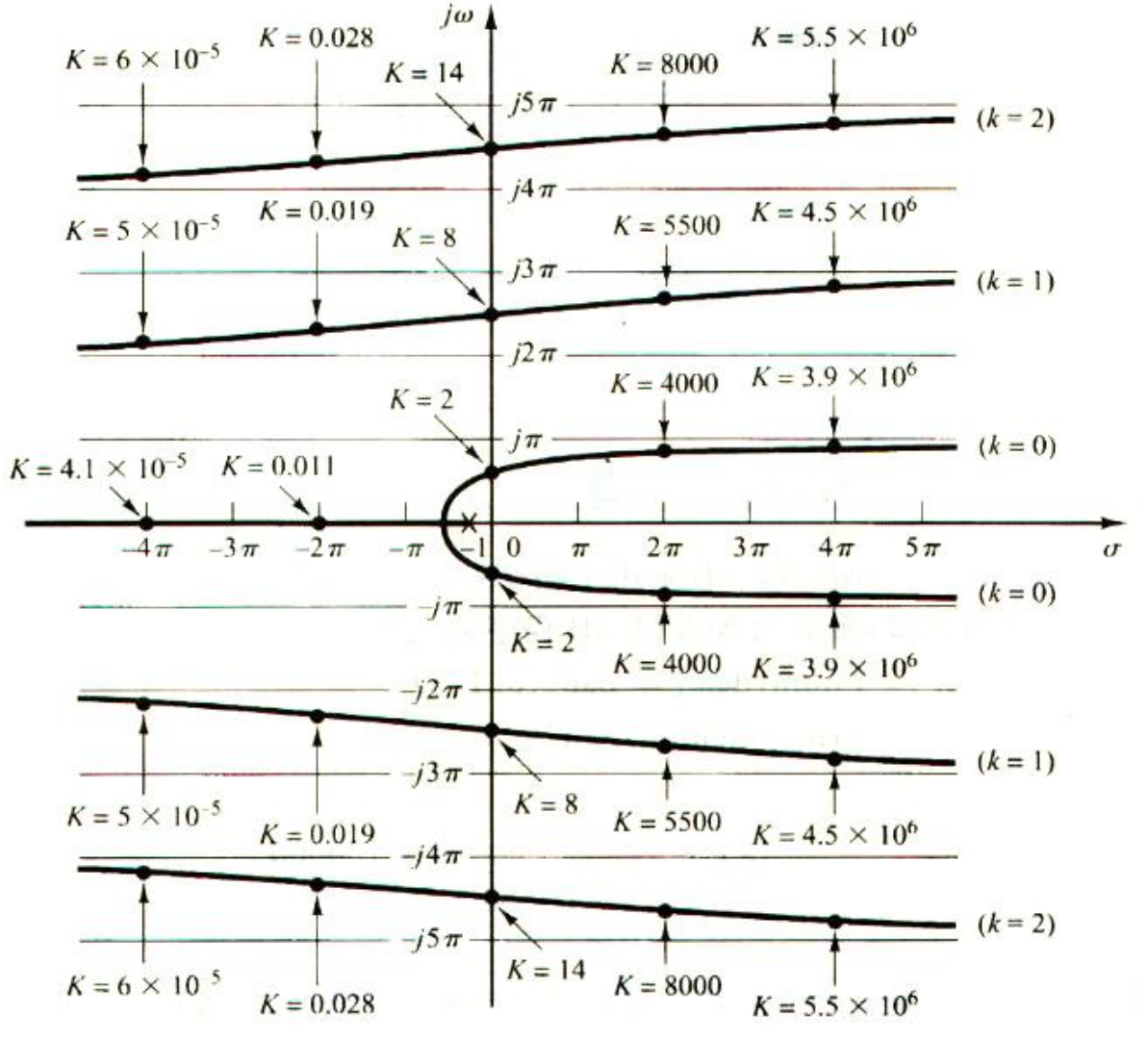
4.7 具有传递延迟 (Transport Lag) 的系统

• 延迟（纯滞后）环节： $y(t) = x(t-T)$，其传递函数为 $e^{-Ts}$。
• 示例： $G(s) = \frac{Ke^{-Ts}}{s+1}$。
• 特征方程： $1 + \frac{Ke^{-Ts}}{s+1} = 0$。
• 辐角条件：
  • $\angle e^{-Ts} - \angle(s+1) = \pm 180^\circ(2k+1)$。
  • 令 $s = \sigma + j\omega$，$e^{-Ts} = e^{-T\sigma} e^{-j\omega T}$。
  • $\angle e^{-Ts} = -\omega T$ (弧度) 或 $-57.3^\circ \omega T$ (度)。
  • 新辐角条件： $-57.3^\circ \omega T - \angle(s+1) = \pm 180^\circ(2k+1) \implies \angle(s+1) = \pm 180^\circ(2k+1) + 57.3^\circ \omega T$
  • 特点：
    1. 辐角条件本身包含 $\omega$，导致根轨迹不再是简单的圆或直线。
    2. 由于 $k=0, 1, 2, ...$，存在无穷多条根轨迹分支。

• 幅值条件：
  • $|\frac{Ke^{-Ts}}{s+1}| = 1 \implies \frac{K |e^{-T\sigma}| |e^{-j\omega T}|}{|s+1|} = 1$。
  • $|e^{-j\omega T}|=1$，$|e^{-T\sigma}| = e^{-T\sigma}$。
  • $K = |s+1| e^{T\sigma}$。
• 近似处理 (当 $T$ 很小时)：
  • $e^{-Ts} \approx 1 - Ts$
  • $e^{-Ts} \approx \frac{1}{Ts+1}$
  • Padé 近似 (更精确)： $e^{-Ts} \approx \frac{1 - Ts/2}{1 + Ts/2} = \frac{2-Ts}{2+Ts}$。这是一个 RHP 零点在 $s=2/T$ 的非最小相位环节。