Rookie's blog

Chapter7-3

自动控制原理笔记：频率响应设计与校正

1. 引言与基础概念

1.1 频率响应设计的目的

在控制系统中，瞬态响应（如超调量、调节时间）通常是最重要的指标。虽然频率响应法通过间接方式描述瞬态特性，但因其方便性，常用于通过伯德图（Bode Plot）进行系统设计。

主要频域指标与系统特性的关系：

  • 低频区（远低于增益交界频率）：表征闭环系统的稳态特性（稳态精度/稳态误差）。

  • 中频区（增益交界频率附近）：表征闭环系统的相对稳定性（相位裕量、增益裕量、谐振峰值）。

  • 高频区（远高于增益交界频率）：表征系统的复杂性及抗噪声能力 。

1.2 伯德图设计的一般步骤

  1. 调整开环增益 KK，以满足稳态精度（如静态误差常数）的要求。
  2. 绘制未校正系统的伯德图。
  3. 若相位裕量或增益裕量不满足要求，则通过引入校正装置改变开环传递函数。
  4. 校正的实质：在稳态精度与相对稳定性之间寻求折中。
    • 校正的目标：在低频区和增益交界频率附近，增益应该足够大，伯德图中对数幅值曲线的斜率应为-20dB/十倍频程。该斜率应延伸到足够的带宽，以保证适当的相位裕量。在高频区域，应当使增益尽可能快衰减下来，以便使噪声的影响达到最小。
image-20251229083314194

2. 超前校正 (Lead Compensation)

2.1 特性与传递函数

超前校正主要用于改善瞬态响应（增加带宽、提高响应速度），但会增强高频噪声效应 。

  • 传递函数：

Gc(s)=KcαTs+1αTs+1=Kcs+1Ts+1αTG_{c}(s)=K_{c}\alpha\frac{Ts+1}{\alpha Ts+1}=K_{c}\frac{s+\frac{1}{T}}{s+\frac{1}{\alpha T}}

其中 0<α<10 < \alpha < 1。零点位于 s=−1/Ts=-1/T，极点位于 s=−1/(αT)s=-1/(\alpha T)。由于 α<1\alpha < 1，零点总是位于极点的右方（更靠近虚轴）。

  • 正弦传递函数：

Gc(jω)=jωT+1jωαT+1, 0<α<1G_c(j\omega) = \frac{j\omega T + 1}{j\omega \alpha T + 1}, \, 0 < \alpha < 1

  • 通常 α\alpha 取值在 0.05 左右。
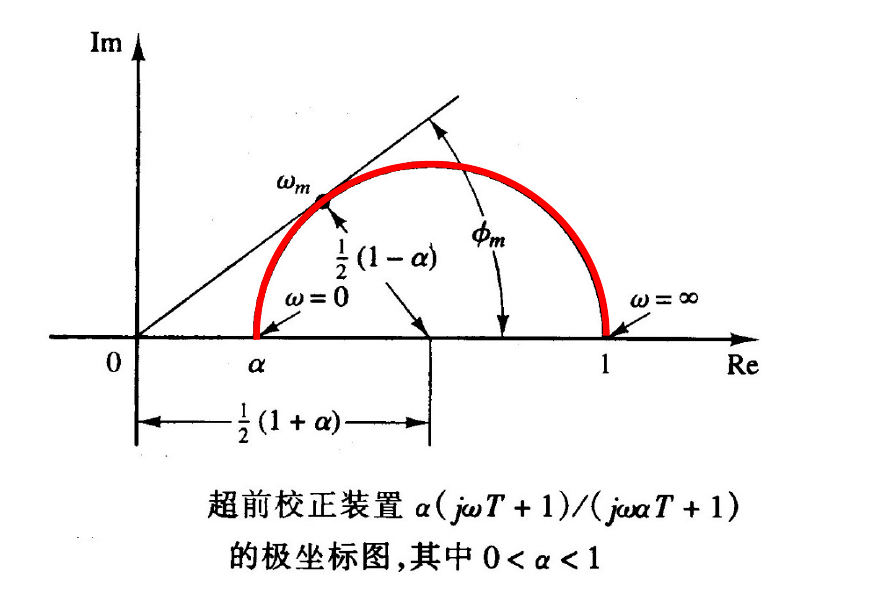
image-20251229085505842

  • 最大相位超前角 ϕm\phi_m：发生在两个转角频率的几何中点 ωm\omega_m 处：

    ωm=1αTsin⁡ϕm=1−α1+α\omega_{m}=\frac{1}{\sqrt{\alpha}T} \quad \sin \phi_{m} = \frac{1-\alpha}{1+\alpha}

该公式用于根据需要的相位超前量确定 α\alpha 值和 TT 值。

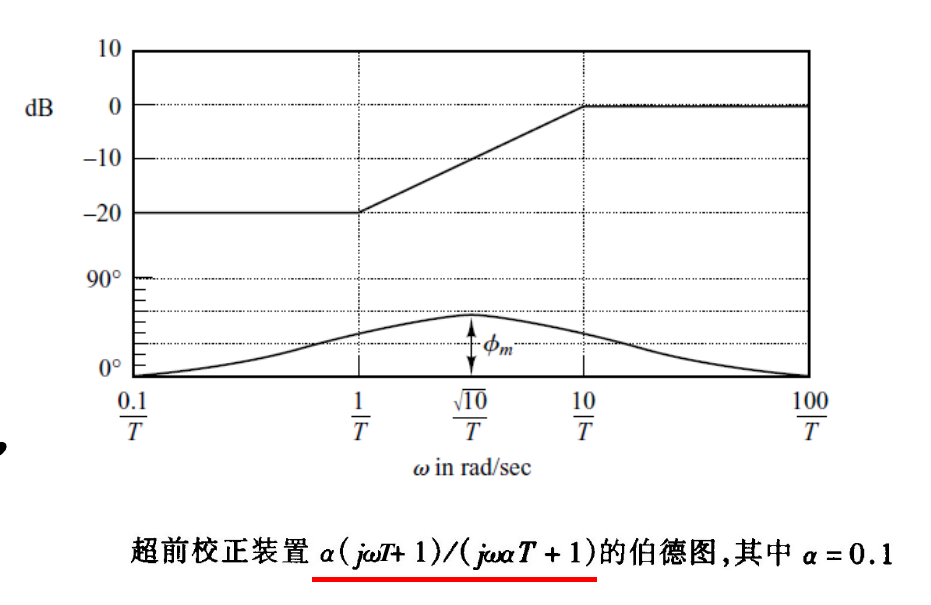
  • 幅频特性：超前校正装置本质上是一个高通滤波器：高频部分通过，低频部分衰减。
    • 0<ω<1T0 < \omega < \frac{1}{T} : 20lg⁡α20 \lg \alpha dB
    • 1T<ω<1αT\frac{1}{T} < \omega < \frac{1}{\alpha T}: 20dB/dec 斜率上升 lg∣G∣=20lg⁡α+20(lg⁡ω−lg1T)lg |G| = 20 \lg \alpha + 20(\lg \omega - lg \frac{1}{T})
    • 1αT<ω<T\frac{1}{\alpha T} < \omega < T: 00 dB
    • 注意：此处给出的幅值中假设 Kc=1K_c = 1，如 Kc≠1K_c \neq 1，需要整体加上 20lg⁡Kc20 \lg K_c dB的偏移量。图中则是假设了 Kc=1K_c = 1 和 α=0.1\alpha = 0.1，故起始段为 −20-20 dB 。
image-20251229085159073

2.2 超前校正设计步骤

  1. 确定增益 KK：根据给定的静态误差常数（如 KvK_v）确定满足稳态要求的开环增益。
    • 定义 K=KcαK = K_c \alpha ，开环系统的静态增益为原来的 K 倍

校正系统的开环传递函数为

Gc(s)G(s)=KTs+1αTs+1G(s)=Ts+1αTs+1G1(s)G_c(s)G(s) = K \frac{Ts+1}{\alpha Ts+1} G(s) = \frac{Ts+1}{\alpha Ts+1} G_1(s)

其中，开环系统的静态增益变成原来的 KK 倍：G1(s)=KG(s)G_1(s) = K G(s)

  1. 画未校正伯德图：利用已确定的 KK，画出系统 G1(jω)G_1(j\omega) 的伯德图，并计算当前的相位裕量 15。

  2. 确定所需超前角：

ϕm=目标相位裕量−未校正系统相位裕量+Δ\phi_m = \text{目标相位裕量} - \text{未校正系统相位裕量} + \Delta

其中 Δ\Delta 是为了补偿因高频增益上升，增益交界频率右移而增加的相位滞后，通常取 5∘∼12∘5^\circ \sim 12^\circ（例题中取了 5∘5^\circ） 。

  1. 计算 α\alpha：利用 sin⁡ϕm=1−α1+α\sin \phi_m = \frac{1-\alpha}{1+\alpha} 求出 α\alpha 。

  2. 确定新的增益交界频率 ωc\omega_c： 在未校正系统的伯德图上，找到幅值为 −10lg⁡(1/α)-10 \lg(1/\alpha) dB（即 −20lg⁡(1/α)-20 \lg(1/\sqrt{\alpha}) dB）的频率点，该点即为新的增益交界频率。同时令 ωm=ωc\omega_m = \omega_c，把超前校正装置提供最大超前相角的频率适配到增益交界频率上

解释：超前校正装置在最大超前角频率 ωm\omega_m 处的幅值增益为 1/α1/\sqrt{\alpha}。为了使校正后系统在该频率处穿越 0dB 线，未校正系统的幅值需为 −10lg⁡(1/α)-10\lg(1/\alpha) dB。

  1. 确定 TT：由 ωc=1αT\omega_c = \frac{1}{\sqrt{\alpha}T} 计算 TT 。

  2. 得出校正装置：用计算好的极点 1/(αT)1/(\alpha T) 和零点 1/T1/T，并计算 Kc=K/αK_c = K/\alpha 。

2.3 实例 (Pages 16-23)

  • 对象：G(s)=4s(s+2)G(s) = \frac{4}{s(s+2)}
  • 指标：Kv=20K_v=20, PM≥50∘PM \ge 50^\circ, GM≥10dBGM \ge 10dB.
  • 结果：校正后系统带宽增加（截止频率从6.3 rad/s增加到9 rad/s），谐振频率增大，谐振峰幅值 MrM_r 减小，相对稳定性得到改善且响应速度变快。
  • 局限性：如果在增益交界频率附近，G1(jω)G_1(j\omega) 的相角减小得很快，超前校正就无效了，因为随着增益交界频率向右方移动，使其在新的增益交界频率上很难产生足够的相位超前去cover掉 G1(jω)G_1(j\omega) 在这一段上增加的相位滞后。
    • 用小 α\alpha 值，但也不能太小（不应小于0.05），否则会导致起始段的增益太低（前面提过起始段 20lg⁡α20 \lg \alpha dB），需要给系统添加很大的附加增益 KcK_c 才能满足稳态性能要求。
    • 如果一个不行，就考虑两个超前校正网络串联（需隔离）

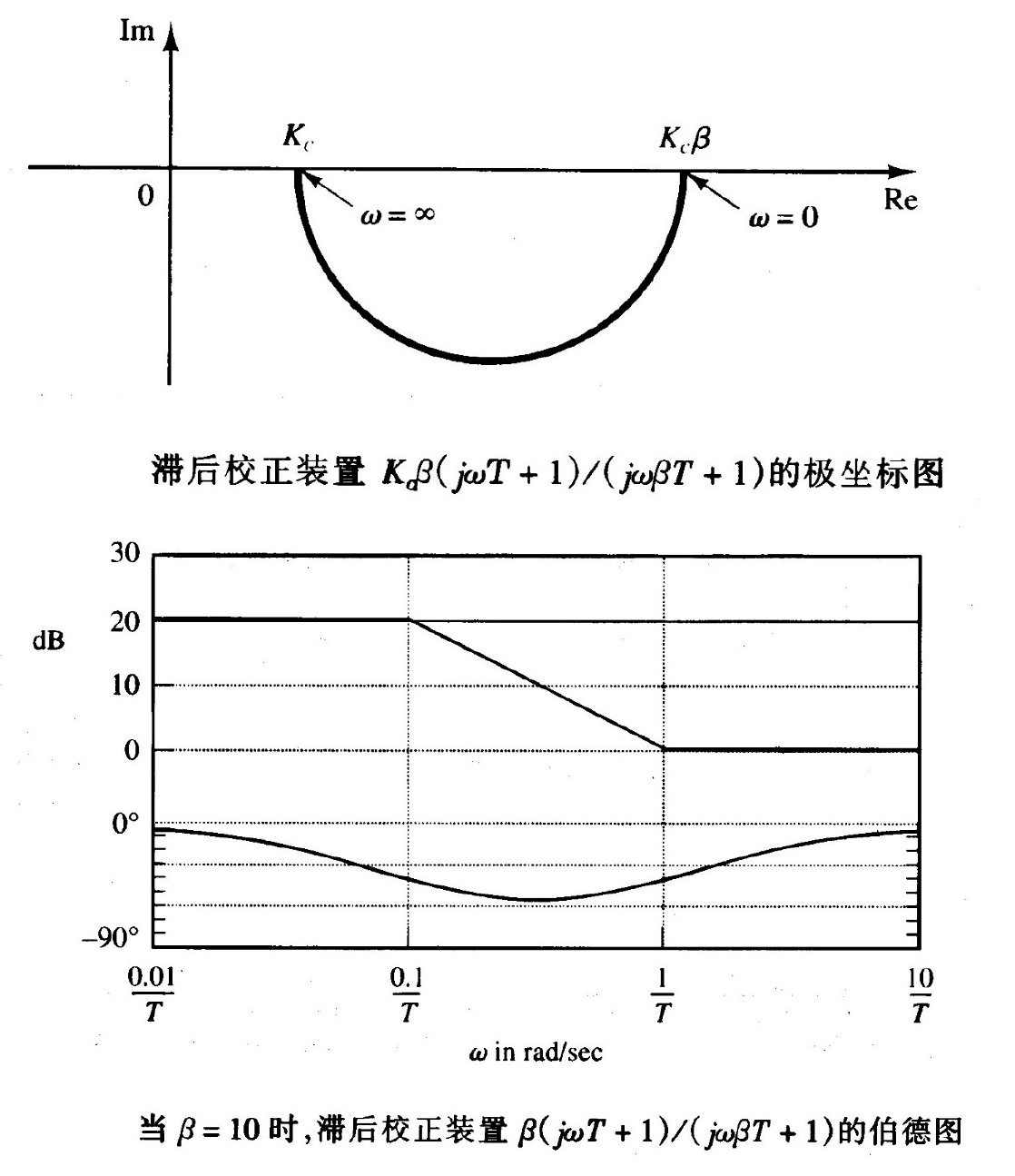
3. 滞后校正 (Lag Compensation)

3.1 特性与传递函数

滞后校正主要用于显著提高稳态精度，同时抑制高频噪声，但会减小系统带宽，导致瞬态响应变慢。

  • 传递函数：

Gc(s)=KcβTs+1βTs+1=Kcs+1Ts+1βTG_{c}(s)=K_{c}\beta\frac{Ts+1}{\beta Ts+1}=K_{c}\frac{s+\frac{1}{T}}{s+\frac{1}{\beta T}}

其中 β>1\beta > 1。极点位于零点的右边（更靠近原点）。

  • 频率特性：
    • 低频（ω<1βT\omega < \frac{1}{\beta T}）幅值为 20lg⁡β20 \lg \beta dB，高频（ω>1T\omega > \frac{1}{T}）幅值为 0 dB，中间段 −20-20 dB/dec 斜率。
      • 此处没有考虑 KcK_c ，考虑 KcK_c 的话需要整体叠加上 20lg⁡Kc20 \lg K_c dB的偏移量。按照滞后校正标准设计方法 Kc=KβK_c = \frac{K}{\beta} ，这相当于把低频增益对齐到 20lg⁡K20 \lg K dB ，而高频段进行衰减。
    • 本质上是一个低通滤波器。
    • 关键作用：利用其在高频段的衰减特性，降低增益交界频率，使系统获得足够的相位裕量（相位滞后特性在校正中是不希望的副作用）。
image-20251229105122378

3.2 滞后校正设计步骤

  1. 确定增益 KK：根据静态误差常数要求确定 KK。
  2. 寻找新的增益交界频率：在未校正系统 G1(jω)G_1(j\omega) 的相频曲线上，找到相角等于 −180∘+目标相位裕量+Δ-180^\circ + \text{目标相位裕量} + \Delta 的频率点，作为新的增益交界频率。
    • Δ\Delta 为补偿滞后校正带来的相位滞后，通常取 5∘∼12∘5^\circ \sim 12^\circ 。
  3. 确定转角频率（零点）： 为避免滞后影响，将滞后校正的零点 ω=1/T\omega = 1/T 选在远低于新加益交界频率处（通常低一个到十个倍频程，例如 ωnew_c/10\omega_{new\_c} / 10）。
    • 反正，我们希望滞后校正的零点离新的增益交界频率尽可能远一些，以避免滞后校正附带的相位滞后，因为我们只想利用滞后校正带来的幅值衰减，而附加的相位滞后是我们不想要的。
  4. 确定 β\beta 值：测量未校正系统在新交界频率处的幅值 AA (dB)。滞后装置需提供 −A-A dB 的衰减以使该处成为 0dB 交叉点。即 20lg⁡(1/β)=−A⇒20lg⁡β=A20 \lg (1/\beta) = -A \Rightarrow 20 \lg \beta = A 。
  5. 确定极点与 KcK_c： 极点 ωp=1/(βT)\omega_p = 1/(\beta T)。增益 Kc=K/βK_c = K/\beta 。

3.3 实例 (Pages 34-41)

  • 对象：G(s)=1s(s+1)(0.5s+1)G(s) = \frac{1}{s(s+1)(0.5s+1)}
  • 指标：Kv=5K_v=5, PM≥40∘PM \ge 40^\circ.
  • 结果：未校正系统不稳定（PM = -20度）。校正后系统稳定，但增益交界频率从2 rad/s 降至 0.5 rad/s，带宽减小，响应速度变慢。

4. 滞后-超前校正 (Lag-Lead Compensation)

4.1 特性与传递函数

综合了超前和滞后校正的优点：既能改善稳态精度（低频增益大），又能增大带宽和稳定性（超前部分） 。

传递函数：

Gc(s)=Kc(s+1T1s+γT1)(s+1T2s+1βT2)G_{c}(s)=K_{c}\left(\frac{s+\frac{1}{T_{1}}}{s+\frac{\gamma}{T_{1}}}\right)\left(\frac{s+\frac{1}{T_{2}}}{s+\frac{1}{\beta T_{2}}}\right)

其中超前部分 γ>1\gamma > 1

s+1T1s+γT1=1γ(T1s+1T1γs+1)γ>1\frac{s+\frac{1}{T_{1}}}{s+\frac{\gamma}{T_{1}}} = \frac{1}{\gamma} \left(\frac{T_1 s + 1}{\frac{T_1}{\gamma}s+1}\right) \quad \gamma > 1

滞后部分 β>1\beta > 1

s+1T2s+1βT2=β(T2s+1βT2s+1)β>1\frac{s+\frac{1}{T_{2}}}{s+\frac{1}{\beta T_{2}}} = \beta \left( \frac{T_2 s + 1}{\beta T_2 s + 1} \right) \quad \beta > 1

通常设计时为了方便（减少一个可配置参数），取 γ=β\gamma = \beta 。（当然也可以选择 γ≠β\gamma \neq \beta）

  • 相频特性：
    • 当 0<ω<ω10<\omega<\omega_1 时，该校正装置作为一个滞后校正装置，相角滞后。
    • 当 <ω<<\omega< 时，该校正装置作为一个超前校正装置，提供超前相角。
    • 频率 ω1\omega_1 是相角等于 0 时的频率

ω1=1T1T2\omega_1 = \frac{1}{\sqrt{T_1 T_2}}

  • 幅频特性：
    • 滞后校正在低频段，超前校正在中频段（较高频段），两者幅频特性叠加
    • 假设 Kc=1,γ=βK_c = 1, \gamma = \beta，低频 ω<1βT2\omega < \frac{1}{\beta T_2} 和高频 ω>γT1\omega > \frac{\gamma}{T_1} 为 0dB
    • 中间频段增益为 ∣Gc∣=−20lgγ|G_c| = -20 lg \gamma dB
    • 若考虑 KcK_c ，整体叠加 20lg⁡Kc20 \lg K_c 的偏移量
    • 滞后校正过渡段 -20dB/dec，超前校正过渡段 +20dB/dec
    • 整体上类似一个带限滤波器

4.2 设计思路

设定 γ=β\gamma = \beta 进行设计

  • 超前部分（包含 T1T_1）：在增益交界频率附近提供相位超前角，增大相位裕量。

  • 滞后部分（包含 T2T_2）：在增益交界频率附近产生幅值衰减，允许在低频范围内增大增益以提高稳态特性。

  • 设计步骤（基于实例）：

    1. 确定 KK 满足稳态误差。
    2. 选择新的增益交界频率 ωc\omega_c。
    3. 计算在该频率所需的相角超前量，确定超前部分的 α\alpha (即 1/β1/\beta)，此时参数 β=γ\beta = \gamma 就已经确定。
    4. 设计滞后部分（确定滞后部分剩下的时间参数 T2T_2），使其转角频率 1T2\frac{1}{T_2} 远低于 ωc\omega_c（例如选择 T2=100ωcT_2 = \frac{100}{\omega_c} ）。
    5. 利用几何作图法或计算，设计超前部分（确定超前部分的时间参数 T1T_1），使校正装置在 ωc\omega_c 处提供适当的衰减和相位。

5. 各种校正方式的对比总结

特性 超前校正 (Lead) 滞后校正 (Lag) 滞后-超前校正 (Lag-Lead)
主要作用 通过在增益交界频率处提供超前相角（相位超前特性），增加稳定裕量，改善瞬态响应，改善相对稳定性，增加带宽 通过降低高频增益（高频衰减特性），允许增大总增益，从而提高稳态精度，抑制高频噪声 兼顾稳态精度与快速响应
带宽变化 增大 (响应快) 减小 (响应慢) 适中/增大
频率特性 高通滤波器 低通滤波器 带限滤波器
信噪比 对高频噪声敏感 (信噪比变差) 衰减高频噪声 (信噪比变好) -
增益需求 需要（往往较大的）附加增益 不需要很大的附加增益 -
适用场景 需快速响应系统 允许响应较慢但要求高精度的系统 要求高精度且快速响应的系统

6. 特殊情况与注意事项

6.1 开环与闭环截止频率的区分

  • 开环截止频率（剪切频率）：开环幅频特性穿越 0dB 线的频率。
  • 闭环截止频率：闭环幅值响应降至低频幅值 -3dB (0.707) 时的频率。
  • 关系：闭环截止频率 > 开环截止频率，且二者同向变动。
    • 特别地，一阶系统相位裕度 ϕ=90∘\phi = 90^{\circ} 时，闭环截止频率 = 开环截止频率。一般来说，二阶及以上系统

6.2 极点抵消 (Pole Cancellation)

  • 原理：利用串联校正装置的零点（或极点）抵消系统中不希望的极点（或零点）。

  • 限制：

    • 不能抵消右半平面（不稳定）的极点。

      • 由于极点和零点位置的不精确性, 几乎不可能将极点与零点完全抵消。若没有完全抵消，则系统的响应中包含随时间增加而逐渐增大的指数项，最终将导致系统的不稳定。

    • 由于元件参数不精确，完全抵消很难实现。未完全抵消的靠近虚轴的二阶共轭极点可能导致长尾的瞬态响应。

      • 不过，如果左半 s 平面内的极点被抵消得不彻底，未被完全抵消的极-零点组合将产生一个持续时间很长但幅值很小的瞬态响应分量，仍然属于正常情况，所以这样做是合理的。

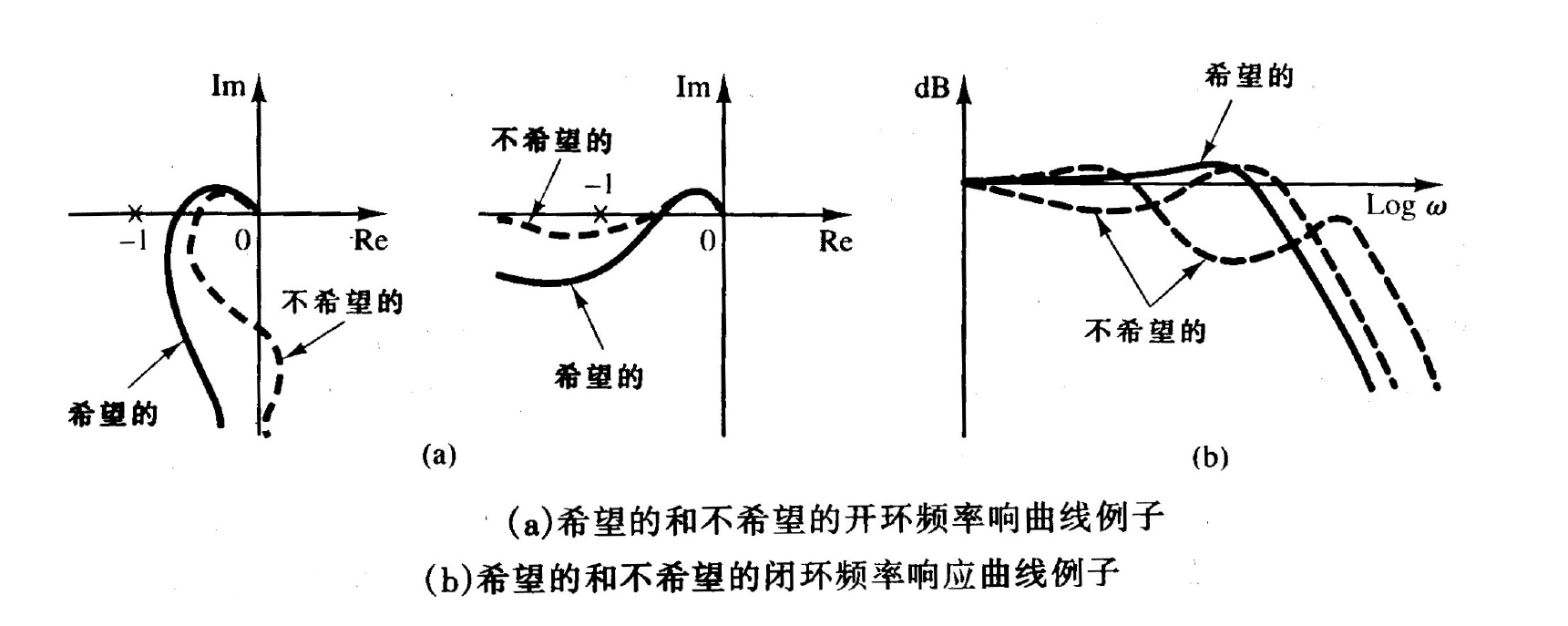
    • 正弦传递函数全频域幅值都为1的控制系统（全通滤波器）只存在于理想情况中，实际不可能做到（能量传递不可能无限快，高频必有衰减）。

      • 而且因为（高频）噪声几乎总是以某种形式存在，所以具有单位传递函数的系统也是不希望的，我们还是希望系统在高频段是衰减的。

  • 相关解释：

    • 在多数实际应用中，希望的控制系统应具有一对共轭复数闭环主导极点（低阶近似为欠阻尼二阶系统，有欠阻尼二阶系统的特性），并且具有适当的阻尼比和无阻尼自然频率。

    • 闭环极-零点配置图的重要部分，如闭环主导极点位置的确定，建立在所需系统的性能指标的基础上。

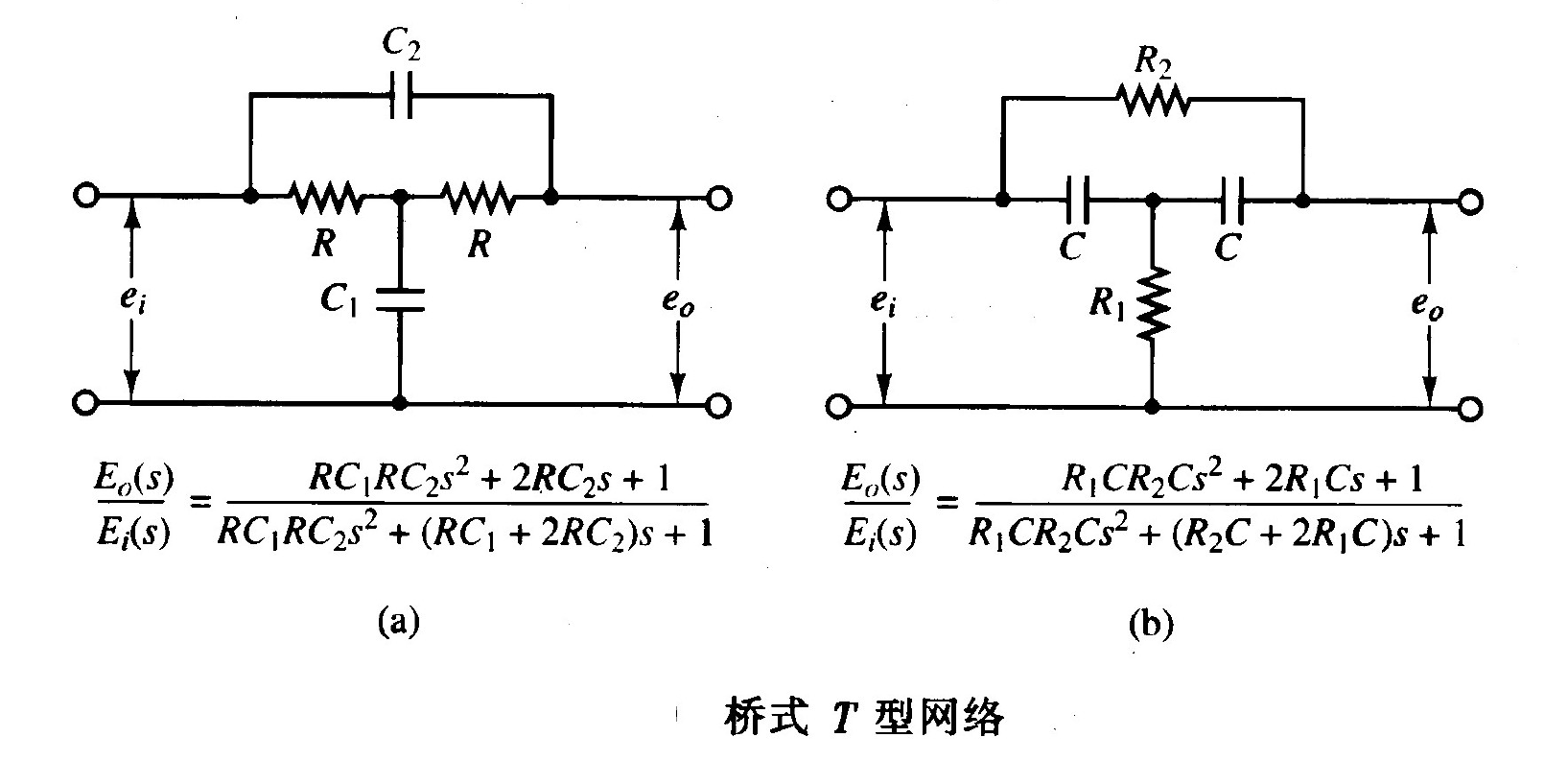
6.3 二阶极点抵消：桥式T型网络 (Bridged-T Network)

  • 当系统包含共轭复数极点（欠阻尼二阶系统特性）时，普通的（只能提供一阶实数零极点的）超前/滞后校正/滞后-超前校正可能效果不佳。
    • 在此情况下，采用具有两个（共轭复数）零点和两个极点的网络。如果零点选择得恰与对象的共轭复数极点相互抵消，则基本上能够以满意的极点取代不希望的极点。
  • 此时（物理实现上）可使用桥式T型网络，它具有两个零点和两个极点，可用于抵消不希望的共轭复数极点。
image-20251229115600094
0%