📚 第七章 频率响应分析 (Frequency-Response Analysis)
本章主要内容包括:
- 引言
- 对数坐标图 (伯德图, Bode Diagrams)
- 极坐标图 (Polar Plots)
- 对数幅-相图 (Log-Magnitude-versus-Phase Plots)
- 奈奎斯特稳定判据 (Nyquist stability criterion)
- 稳定性分析
- 相对稳定性
1. 引言
1.1 核心概念
- 频率响应 (Frequency Response): 指的是系统对正弦输入信号的稳态响应。
- 频率响应法 (Frequency Response Method): 通过在一定范围内改变输入正弦信号的频率,来研究系统产生的响应。
- 优点: 这种方法简单、精确、抗噪声干扰,并且可以推广到非线性控制系统。它与根轨迹法是互为补充的。
- 奈奎斯特稳定判据 (Nyquist Stability Criterion): 一种重要工具,它根据系统开环频率响应特性的信息,来研究线性闭环系统的绝对稳定性和相对稳定性。
1.2 系统对正弦输入的稳态输出
考虑一个稳定、线性、定常(LTI)系统,其传递函数为 G(s)=X(s)Y(s)。
- 输入信号: x(t)=Asin(ωt)。
- 稳态输出信号: 如果系统稳定,其稳态输出 y(t) 必定也是一个同频率的正弦信号,但幅值和相位会发生变化:
y(t)=Bsin(ωt+ϕ)
这里的关键在于 B 和 ϕ 是如何与系统 G(s) 关联的。
- 正弦传递函数 (Sinusoidal Transfer Function): 通过在系统传递函数 G(s) 中用 jω 替换 s 得到,即 G(jω)。
- 幅值关系: 输出幅值 B 是输入幅值 A 乘以 G(jω) 的模。
B=A∣G(jω)∣=AX(jω)Y(jω)
- 相位关系: 输出相位 ϕ 是 G(jω) 的相角。
ϕ=∠G(jω)=∠(X(jω)Y(jω))
因此,系统的频率响应特性可以直接由下式求得。
G(jω)=X(jω)Y(jω)
- ∣G(jω)∣ 被称为幅值比(输出振幅 / 输入振幅)。
- ∠G(jω) 被称为相位移(输出相位 - 输入相位)。
1.3 稳态响应的推导过程
-
输入: x(t)=Asin(ωt)。
-
输入的拉氏变换: X(s)=s2+ω2Aω。
-
输出的拉氏变换: Y(s)=G(s)X(s)=G(s)s2+ω2Aω。
-
部分分式展开: 假设 G(s) 有n个互不相同的极点 −s1,…,−sn, Y(s) 可以展开为:
Y(s)=s+jωa+s−jωaˉ+i=1∑ns+sibi
(其中 aˉ 是 a 的共轭复数)。
-
反变换 (时域响应):
y(t)=稳态部分ae−jωt+aˉejωt+暂态部分i=1∑nbie−sit(t≥0)
-
暂态响应: 对于稳定系统,所有极点 −si 的实部均为负。因此,当 t→∞ 时,所有 e−sit 项(包括重极点情况下的 tn−1e−sjt 项)都趋近于 0。
-
稳态响应 (yss(t)):
yss(t)=ae−jωt+aˉejωt
-
求解系数:
使用留数的方式求解系数
a=s→−jωlim(s+jω)Y(s)=G(−jω)−2jωAω=−2jAG(−jω)
利用系数的共轭性质,
aˉ=2jAG(jω)
- 代入: 令 G(jω)=∣G(jω)∣ejϕ,则其共轭 G(−jω)=∣G(jω)∣e−jϕ。
yss(t)=(−2jA∣G(jω)∣e−jϕ)e−jωt+(2jA∣G(jω)∣ejϕ)ejωt=A∣G(jω)∣[2jej(ωt+ϕ)−e−j(ωt+ϕ)]
- 最终结果: 根据欧拉公式 sin(x)=2jejx−e−jx,可得:
yss(t)=A∣G(jω)∣sin(ωt+ϕ)
这证明了我们在1.2部分中的一系列结论。
1.4 相位超前与滞后
- 相位滞后 (Phase Lag): 相角为负 (ϕ<0)。
- 相位超前 (Phase Lead): 相角为正 (ϕ>0)。
- 实现这些特性的网络分别称为相位滞后网络和相位超前网络。
2. 频率响应的图形表示
有三种主要的图形表示方法:
- 伯德图 (Bode Diagrams): 也称对数坐标图。
- 极坐标图 (Polar Plots): 也称奈奎斯特图 (Nyquist Plots)。
- 对数幅-相图 (Log-Magnitude-versus-Phase Plots): 也称尼科尔斯图 (Nichols Plots)。
3. 伯德图 (Bode Diagrams)
伯德图是应用最广泛的一种图示法。
3.1 伯德图的定义
伯德图由两幅图组成:
- 对数幅值图: 20log∣G(jω)∣,单位是分贝 (dB)。
- 相角坐标图: ∠G(jω),单位是度。
这两幅图都以频率 ω 为横坐标,且频率轴使用对数尺度。纵坐标(幅值/dB或相角/度)则使用线性尺度。
分贝 (dB) 换算:
- 20log(K×10)=20logK+20 dB (数值增大10倍,增加20 dB)。
- 20log(K×10n)=20logK+20n dB。
- 20log(1/K)=−20logK dB (倒数关系,dB值差一个负号)。
3.2 伯德图的优点
- 乘法变加法: 传递函数因子的相乘,在伯德图上表现为对数幅值(dB)的相加。
- 渐近线近似: 可以使用简单的渐近线来快速绘制近似的对数幅值曲线,需要时再进行修正。
- 扩展低频: 对数频率轴可以有效扩展低频范围(但无法画到 ω=0)。
- 实验辨识: 易于通过实验数据确定传递函数。
3.3 绘制伯德图的基本因子
任何一个传递函数 G(jω) 都可以分解为以下四种基本因子的乘积:
- 增益 K
- 积分/微分因子 (jω)∓1
- 一阶因子 (1+jωT)∓1
- 二阶因子 [1+2ζ(jω/ωn)+(jω/ωn)2]∓1
3.4 因子 1: 增益 K
- 对数幅值: 20logK (dB)。这是一条不随 ω 变化的水平直线。
- 相角: 0∘。
- 影响: 改变 K 值,只会使整个对数幅值曲线上升或下降 20logK dB,不影响相位曲线。
3.5 因子 2: 积分/微分因子 (jω)∓n
频率单位:
- 倍频程 (Octave): 频率从 ω1 变到 2ω1。
- 十倍频程 (Decade): 频率从 ω1 变到 10ω1。
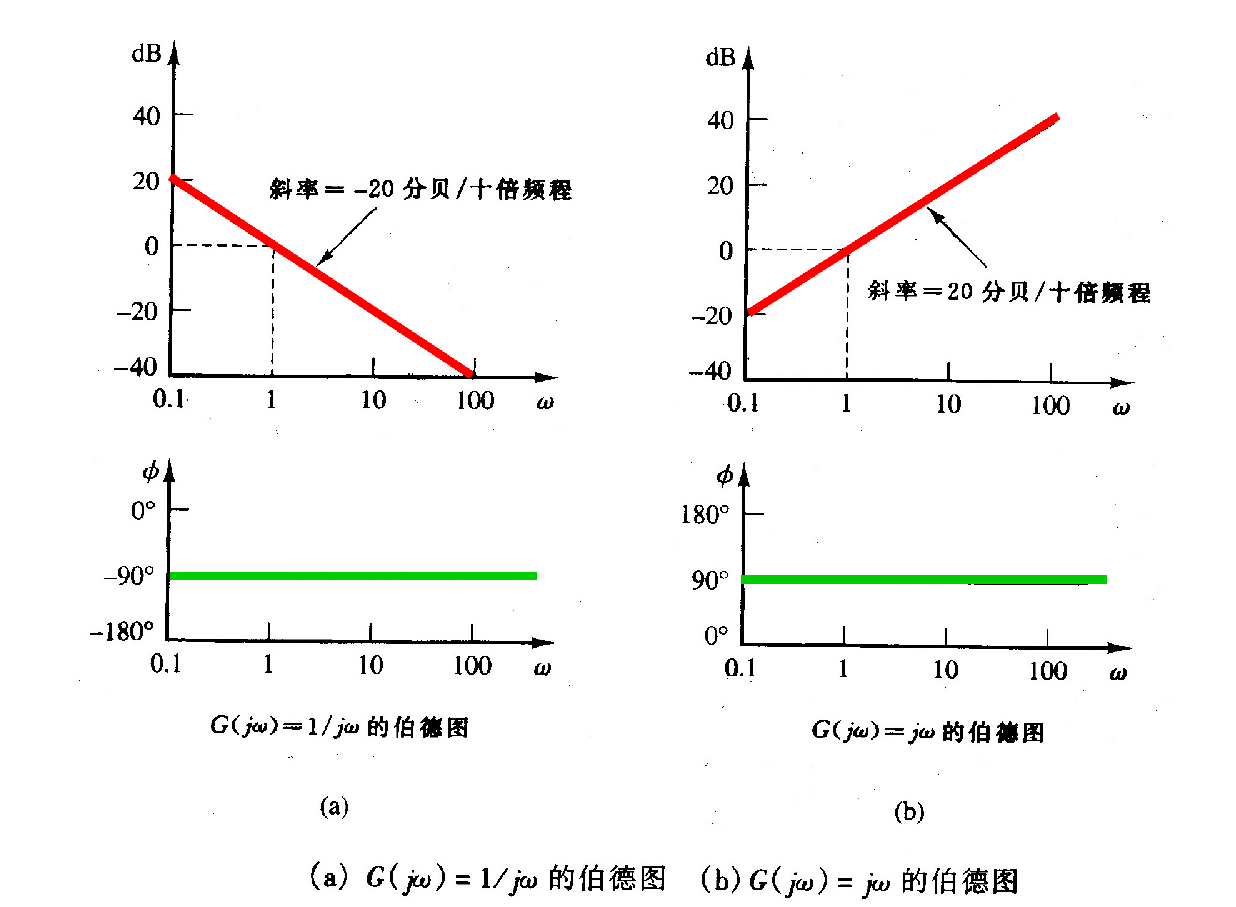
A. 积分因子 (jω)−n (以 n=1 为例, 1/jω)
- 对数幅值: 20log∣1/jω∣=−20logω (dB)。
- 图形: 这是一条直线,斜率为 -20 dB/十倍频程 (或 -6 dB/倍频程)。
- 特征点: 该直线在 ω=1 时穿过 0 dB 轴。
- 相角: ∠(1/jω)=−90∘(恒定)。
B. 微分因子 (jω)n (以 n=1 为例, jω)
- 对数幅值: 20log∣jω∣=20logω (dB)。
- 图形: 这是一条直线,斜率为 +20 dB/十倍频程 (或 +6 dB/倍频程)。
- 特征点: 该直线在 ω=1 时穿过 0 dB 轴。
- 相角: ∠(jω)=+90∘(恒定)。
C. 一般情况 (jω)∓n
- (jω)−n: 幅值斜率为 −20n dB/十倍频程,相角为 −90∘×n。
- (jω)n: 幅值斜率为 +20n dB/十倍频程,相角为 +90∘×n。
![image-20251106104300375]()
3.6 因子 3: 一阶因子 (1+jωT)∓n
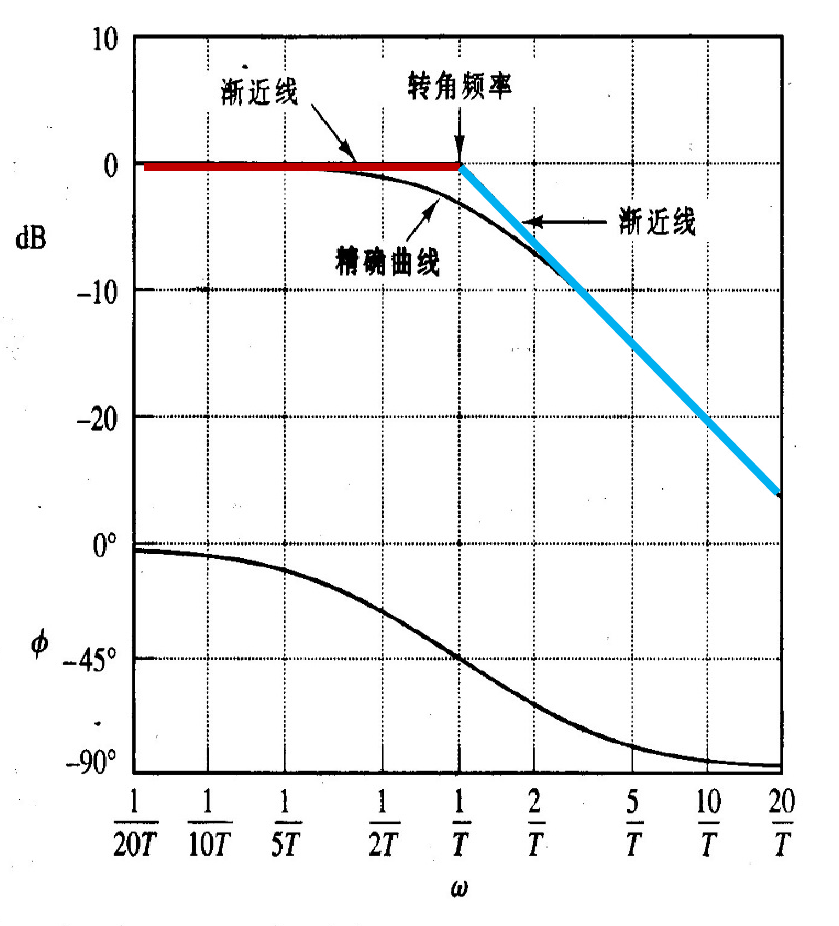
A. 因子 (1+jωT)−1 (低通滤波器特性)
![image-20251227162932644]()
20log1+jωT1=−20log1+(ωT)2
- 渐近线 (Asymptotes):
- 低频 (ω≪1/T): 幅值 ≈−20log1=0 dB。这是一条0 dB水平线。
- 高频 (ω≫1/T): 幅值 ≈−20log(ωT)。这是一条斜率为 -20 dB/十倍频程的直线。
- 转角频率 (Corner Frequency): 两渐近线相交于 ω=1/T。此处也称为交接频率或断点频率。
- 精确曲线修正 (误差):
- 在转角频率 ω=1/T 处:精确值为 −20log1+12=−20log2≈ -3.03 dB。这是误差最大的点,误差为 -3.03 dB。
- 在 ω=1/(2T) (低一倍频程):误差 ≈ -0.97 dB。
- 在 ω=2/T (高一倍频程):误差 ≈ -0.97 dB。
- 相角: 精确相角为 ϕ=−arctan(ωT)。
- 零频率 ω=0: ϕ=0∘。
- 转角频率 ω=1/T: ϕ=−arctan(1)=−45∘。
- 频率无穷大 ω=∞: ϕ=−90∘。
- 该曲线关于点 (ω=1/T,ϕ=−45∘) 斜对称。(因为相角是以反正切函数表示的)
B. 因子 (1+jωT)+1
- 其伯德图恰好是 (1+jωT)−1 的相反数(关于 0 dB 和 0° 轴对称)。
- 对数幅值: 20log∣1+jωT∣
- 渐近线: 0 dB 水平线,在 ω=1/T 转折为 +20 dB/十倍频程的斜线。
- 相角: ϕ=+arctan(ωT)
- ω=0: ϕ=0∘。
- ω=1/T: ϕ=+45∘。
- ω=∞: ϕ=+90∘。
C. 一般情况 (1+jωT)∓n
- 转角频率仍为 ω=1/T。
- 高频渐近线斜率为 ∓20n dB/十倍频程。
- 误差会叠加:在任意频率点的误差或相角,是 n=1 情况下的 n 倍。
3.7 因子 4: 二阶因子
[1+2ζ(jωnω)+(jωnω)2]∓1
我们重点分析 0<ζ<1 (欠阻尼) 的情况,因为临界阻尼和过阻尼可以直接分解成两个一阶因子处理。
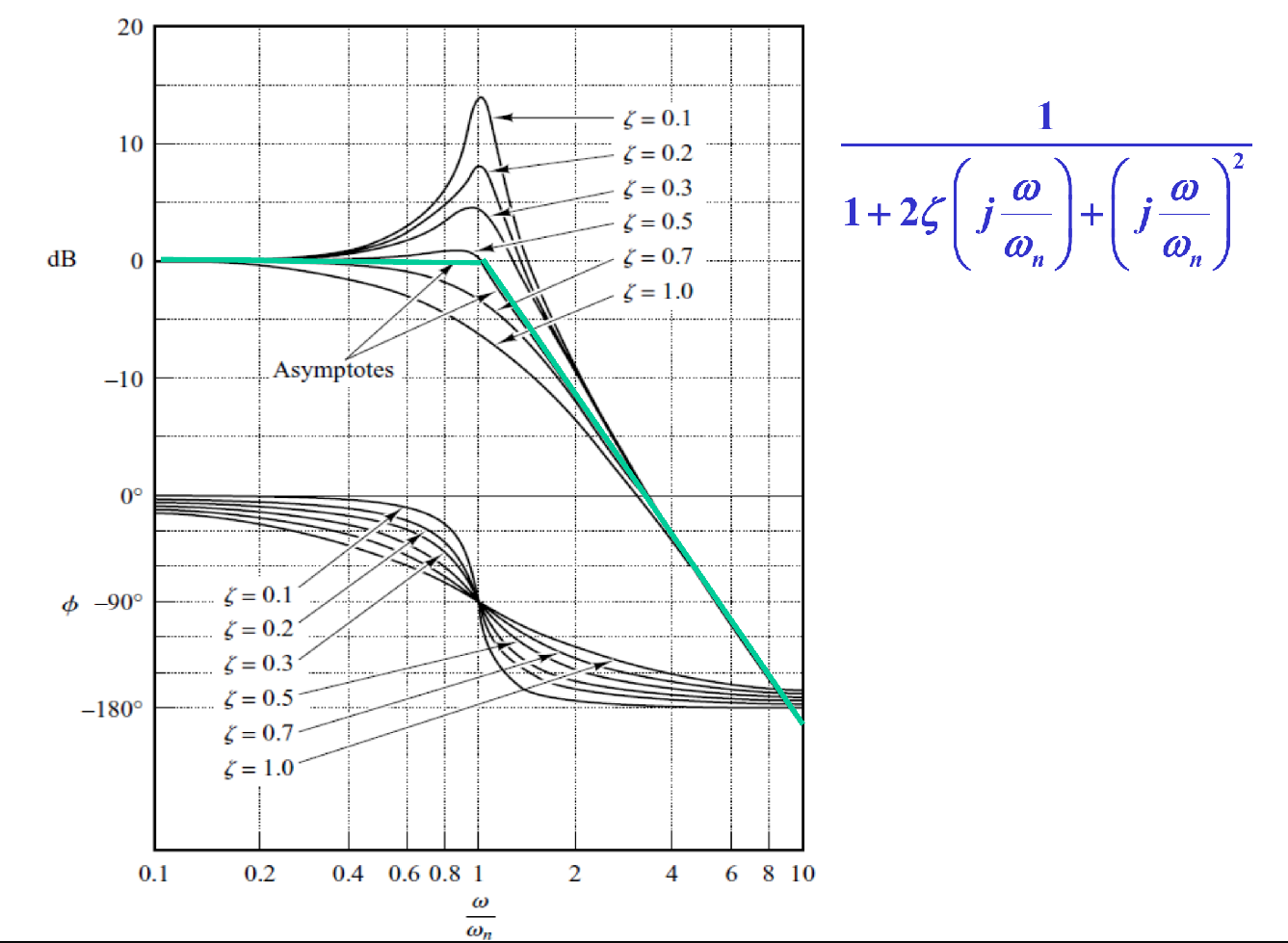
A. 因子 [1+2ζ(jωnω)+(jωnω)2]−1
控制系统常具有以下标准二阶因子的形式
1+2ζ(jωnω)+(jωnω)21
![image-20251111104742288]()
∣G(jω)∣=(1−ωn2ω2)2+(2ζωnω)21
20log1+2ζ(jωnω)+(jωnω)21=−20log(1−ωn2ω2)2+(2ζωnω)2
- 渐近线:
- 低频 (ω≪ωn): 幅值 ≈0 dB。
- 高频 (ω≫ωn): 幅值 ≈−20log(ωn2ω2)=−40log(ωnω)。这是一条斜率为 -40 dB/十倍频程 的直线。
- 转角频率: 两渐近线相交于 ω=ωn(无阻尼自然频率)。ωn 即为二阶因子的转角频率。
- 精确曲线修正: 对于 ζ<0.707 的二阶因子,频率响应表示是很不精确的,谐振峰值会被漏掉。
- 精确曲线的形状严重依赖于阻尼比 ζ。
- 当 ζ 很小 (如 ζ=0.1,0.2) 时,在 ωn 附近会产生一个明显的峰值。
- 当 ζ 较大 (如 ζ=0.7,1.0) 时,曲线平滑过渡。
- 相角表达式:
ϕ=−arctan[1−(ωnω)22ζωnω]
- 相角特性:
- ω=0: ϕ=0∘。
- ω=ωn: ϕ=−arctan(02ζ)=−90∘。注意:在转角频率处的相角恒为-90°,与 ζ 无关。
- ω=∞: ϕ=−180∘。
- 该曲线关于点 (ω=ωn,ϕ=−90∘) 斜对称。
- 总的相位变化量为 −180∘
B. 谐振频率 (ωr) 与 谐振峰值 (Mr)
- 谐振频率 ωr: 幅值 ∣G(jω)∣ 达到峰值的频率。
- 推导:∣G(jω)∣ 取最大值,等效于其分母上的 g(ω)=(1−ωn2ω2)2+(2ζωnω)2 取最小值。
∣G(jω)∣=(1−ωn2ω2)2+(2ζωnω)21=g(ω)1⟹g(ω)=(1−ωn2ω2)2+(2ζωnω)2
通过求导或配方可得 g(ω) 在 ω=ωn1−2ζ2 处取最小值。
令 u=ωn2ω2,然后进行配方
g(ω)=(1−u)2+4ζ2u=u2+(4ζ2−2)u+1=[u+(2ζ2−1)]2+4ζ2(1−ζ2)
得到
g(ω)=[ωn2ω2−(1−2ζ2)ωn2]2+4ζ2(1−ζ2)
当 ω2=ωn2(1−2ζ2)⟹ω=ωn1−2ζ2 时,g(ω)min=4ζ2(1−ζ2),此时幅值最大(达到谐振峰值) ∣G(jω)∣max=2ζ1−ζ21
ωr=ωn1−2ζ2
- 关于谐振频率的理解:
- 此公式仅在 1−2ζ2≥0,即 0≤ζ≤0.707 时有意义,即只有 0≤ζ≤0.707 时存在谐振峰。
- 当 ζ>0.707 时,不产生谐振峰值,幅值曲线单调下降。
- 当 0<ζ≤0.707 时,谐振频率 ωr 小于转角频率/无阻尼自然频率 ωn 。
- 当阻尼比逐渐减小至0,即 ζ→0 时,ωr 逐渐变大,接近无阻尼自然频率 ωr→ωn 。ζ=0 时(无阻尼系统),谐振频率等于无阻尼自然频率 ωr=ωn,此时幅值会变成无穷大。
- 谐振峰值 Mr: 将 ωr 代入 ∣G(jω)∣ 得到峰值。
Mr=2ζ1−ζ21
- 关于 Mr 公式的理解:
- Mr 只与阻尼比 ζ 有关
- 当 ζ→0 时,Mr→∞。这表明无阻尼系统在其自然频率 ωn 上被激励而振荡时,G(jω) 的幅值将变成无穷大,即所谓的共振现象。
- 当 ζ=0.707 时,Mr=1 (即 0 dB)。这是产生谐振峰的临界点。ζ>0.707 时不产生谐振峰。
- 谐振时的相角:
∠G(jωr)=−arctan[ζ1−2ζ2]=−90∘+arcsin1−ζ2ζ
C. 因子 [1+2ζ(jωnω)+(jωnω)2]+1
- 其伯德图是上一节中 [...]−1 情况的相反数。
- 渐近线斜率从 0 dB/十倍频程变为 +40 dB/十倍频程。
- 相角从 0∘ 变化到 +180∘。
3.8 绘制伯德图的一般步骤
- 标准化: 将 G(jω) 改写成基本因子的乘积形式(如 K,(jω)∓n,(1+jωT)∓n 等)。
- 注意基本因子的形式不要搞错,尤其是二阶因子的形式
- 注意系数的处理,不要忘记处理因子的过程中产生的系数
- 找转角频率: 确定所有一阶和二阶因子的转角频率 (ω=1/T 或 ω=ωn)。
- 画幅值渐近线:
- 从低频开始,确定初始斜率(由 (jω)N 因子决定)。
- 按频率从小到大,每经过一个转角频率,渐近线斜率就叠加上该因子高频渐近线的斜率(例如,(1+jωT)−1 使斜率 -20 dB/十倍频程)。
- 修正幅值曲线: 在转角频率附近对渐近线进行修正(如一阶在 ωc 处修正 -3dB,二阶根据 ζ 修正)。
- 画相角曲线: 将所有单个因子的相角曲线代数叠加,得到总的相角曲线。
4. 最小相位与非最小相位系统
4.1 定义
- 最小相位传递函数: 在右半 s 平面内既没有零点也没有极点的传递函数。
- 非最小相位传递函数: 在右半 s 平面内有零点或/和极点的传递函数。
- 最小/非最小相位系统: 分别指具有最小相位传递函数(且不含纯传递延迟因子)/非最小相位传递函数的系统。
- 纯传递延迟因子 (e−sT) 也被认为是非最小相位环节。
4.2 特性
- 相角范围: (不完全严谨)所有具有相同幅值特性的系统中,最小相位系统的相角变化范围是最小的。
- 严谨说法需要加一些额外的限制条件:对于开环极点都在左半s平面,且 q≥p (即物理可实现)的系统(其中 p 和 q 分别表示传递函数中分子和分母多项式的次数),这个结论成立。
- 如果不满足这个附加条件,可以举出一些反例:比如一些有右半平面极点的非最小相位系统的相角变化范围可能比更大
![image-20251227190617915]()
- 唯一性: 其实对于最小相位系统,我们最关心的性质是唯一性。
- 对于最小相位系统,其传递函数可以仅由幅值曲线唯一确定。
- 对于最小相位系统,幅值特性与相角特性是唯一对应的。知道一个就可以唯一确定另一个。
- 对于非最小相位系统,以上结论不成立。
- 用全通滤波器乘任意传递函数,不改变幅值曲线,但改变相角曲线,显然这样就没有唯一性了。
示例 (All-Pass Filter):
考虑以下两个系统
- G1(jω)=1+jωT11+jωT (最小相位,零点在 -1/T)。
- G2(jω)=1+jωT11−jωT (非最小相位,零点在 +1/T)。
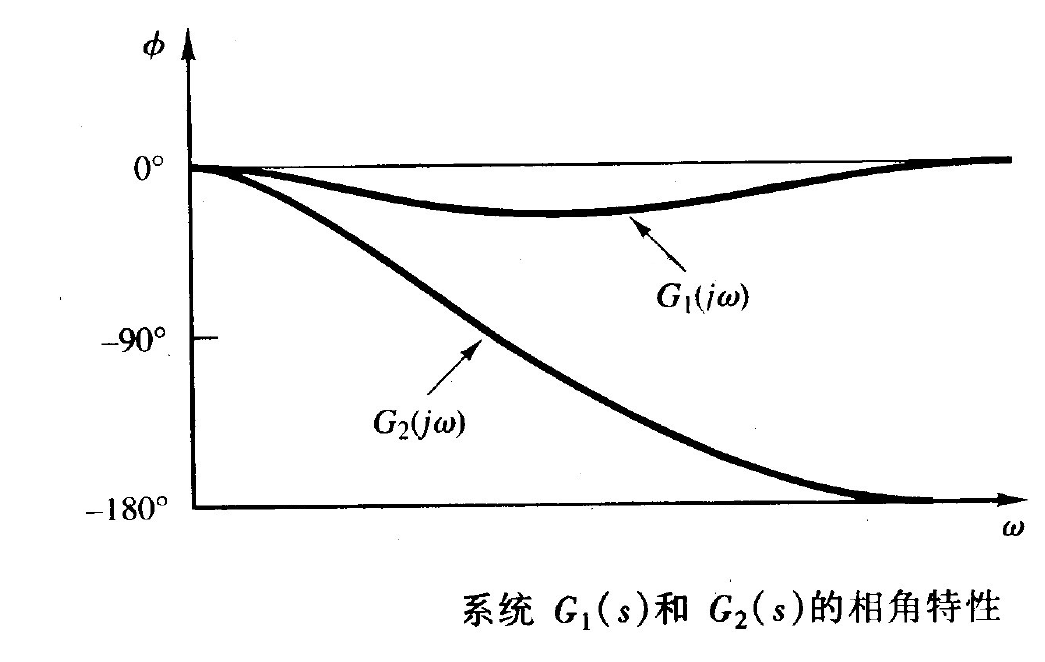
![image-20251227194535440]()
可以发现:
- ∣G1(jω)∣ 和 ∣G2(jω)∣ 幅值曲线完全相同,但 G2(jω) 的相位滞后(负相角)远大于 G1(jω)。
- 两者相差的因子为一个全通滤波器 G(jω)=1+jωT1−jωT,其幅值为1,但相角从 0∘ 变为 −180∘。
所以我们可以得出一些结论:
- 在前面提到过的那个严谨附加条件下,具有相同幅频特性曲线的系统中,非最小相位系统一般呈现出比最小相位系统更大的相位滞后。
4.3 辨识
非最小相位情况可能发生由两种不同来源引入:
- 系统中包含一个或多个非最小相位环节
- 系统中的小回路(内部回路)不稳定
用伯德图辨识(设传递函数分子为p阶,分母为q阶)
- 检查高频幅值特性:在 ω→∞ 时,任何系统的对数幅值曲线斜率都等于 −20(q−p) dB/十倍频程。
- 检查高频相角特性
- 最小相位系统: 在 ω→∞ 时,相角 ϕ∞=−90∘(q−p)。
- 非最小相位系统: 在 ω→∞ 时,相角 ϕ∞=−90∘(q−p)。
- 结论: 必须同时检查高频斜率和高频相角,两者都满足 q−p 的关系时,系统才是最小相位的。
4.4 传递延迟 (Transportation Delay)
- 传递函数: G(jω)=e−jωT。
- 对数幅值: ∣G(jω)∣=1,即 0 dB。是一条水平直线。
- 相角: ϕ=−ωT (弧度) 或 −57.3ωT (度)。
- 特性: 相角随频率线性下降,趋于 −∞。这是一个典型的非最小相位环节,因为它有 0 dB 的幅值(同 G(s)=1),但相角滞后远大于 0∘。
5. 系统类型与伯德图低频特性的关系
对于单位负反馈系统,开环传递函数 G(s) 的低频伯德图特性可以用来确定系统的静态误差常数 (Kp,Kv,Ka)。
Recall:系统的类型 (Type N) 是指 G(s) 在 s=0 处积分因子的个数 N。
G(s)=sN(T1s+1)(T2s+1)…K(Tas+1)(Tbs+1)…
而在正弦传递函数 G(jω) 中,这对应分母上 (jω)N 的次数 N。
G(jω)=(jω)N(T1jω+1)(T2jω+1)…K(Tajω+1)(Tbjω+1)…
正弦传递函数的低频近似
ω→0limG(jω)=(jω)NK
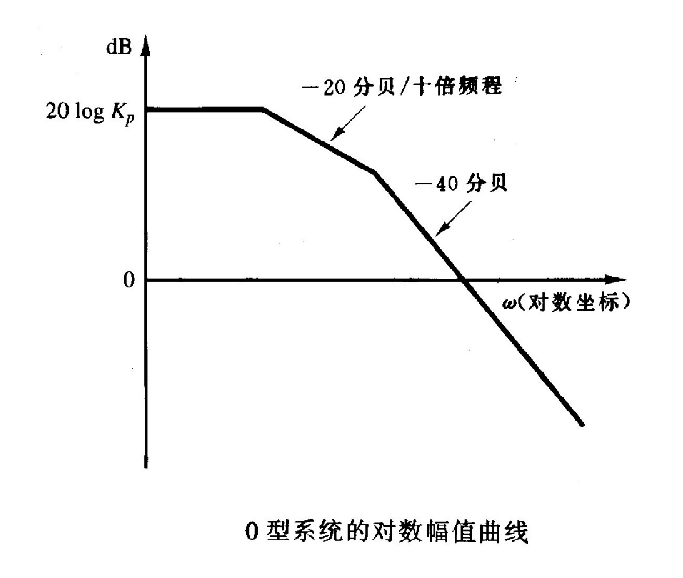
5.1 0 型系统 (N=0)
- 低频特性: limω→0G(jω)=K=Kp (静态位置误差常数)。
- 伯德图: 低频渐近线是一条幅值为 20logKp dB 的水平线 (斜率为 0 dB/十倍频程)。
![image-20251111111630462]()
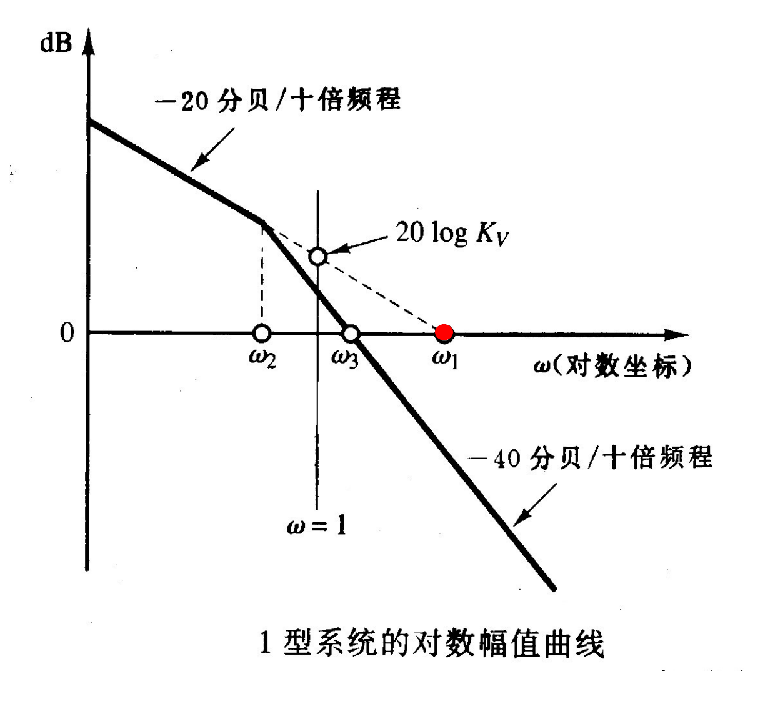
5.2 1 型系统 (N=1)
- 低频特性: (其中 Kv 是静态速度误差常数)
ω→0limG(jω)≈jωKv
- 伯德图: 低频渐近线是一条斜率为 -20 dB/十倍频程 的直线。
- 确定直线方程的方法:由于我们使用的幅频特性曲线是对数刻度的,两边取 log 就好了
∣G(jω)∣=ωKv⟹20log∣G(jω)∣=20logKv−20logω
- 确定 Kv:
- 该 -20 dB/十倍频程的渐近线(或其延长线)在 ω=1 处的幅值,即为 20logKv dB。
- 该 -20 dB/十倍频程的渐近线(或其延长线)与 0 dB 直线相交,交点的频率 ω1 在数值上等于 Kv(即 ω1=Kv)。
![image-20251111111920854]()
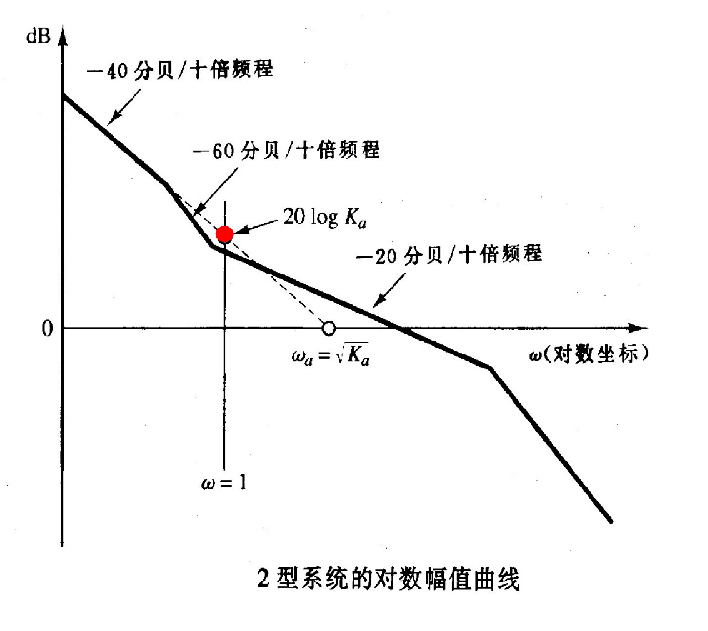
5.3 2 型系统 (N=2)
- 低频特性: (其中 Ka 是静态加速度误差常数)
ω→0limG(jω)≈(jω)2Ka
- 伯德图: 低频渐近线是一条斜率为 -40 dB/十倍频程 的直线。
∣G(jω)∣=ω2Ka⟹20log∣G(jω)∣=20logKa−40logω
- 确定 Ka:
- 该 -40 dB/十倍频程的渐近线(或其延长线)在 ω=1 处的幅值,即为 20logKa dB。
- 该 -40 dB/十倍频程的渐近线(或其延长线)与 0 dB 直线相交,交点的频率 ωa 在数值上等于 Ka(即 ωa=Ka)。
- 读图时可以用这个交点反解 Ka,关系为 Ka=ωa2
![image-20251111113350423]()