Chapter2 number systems

Number Systems

• Decimal Numbers 十进制
• Binary Numbers 二进制
• Hexadecimal Numbers 十六进制

Relationship between hexadecimal and binary

Each hexadecimal digit represents a 4-bit binary number.

所以二进制和十六进制可以方便地互相转换

Conversion of Number Systems

Decimal-to-Binary Conversion

Converting Decimal Whole Number to Binary 十进制整数转二进制

Sum-of-Weights Method

就是按照二进制每一位的权重凑数，简单的数可以这样直接看

Repeated Division-by-2 Method

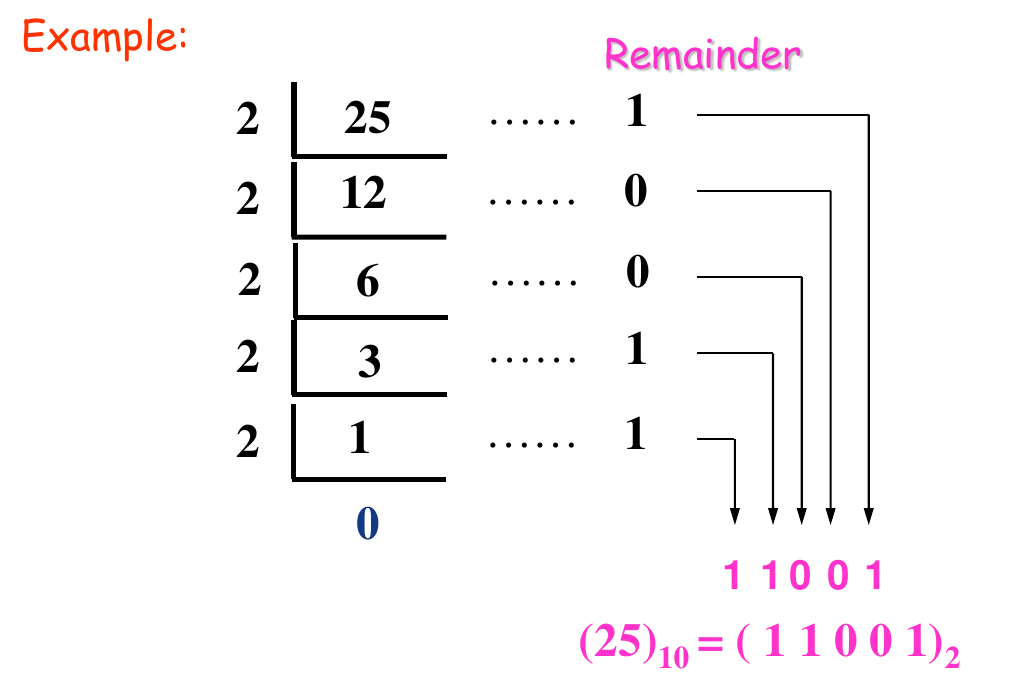
• For a given decimal whole number, to convert it to binary, begin by dividing it by 2. Then divide each quotient by 2 until there is a 0 whole-number quotient.
• The remainders generated by each division form the binary number.
• The first remainder to be produced is the least significant bit(LSB) in the binary number, and the last remainder to be produced is the MSB .
• MSB: Most Significant Bit 最高位
• LSB: Least Significant Bit 最低位
• 说人话，具体的实现方式是：短除法

Converting Decimal Fractions to Binary 十进制分数（小数）转二进制

Sum-of-Weights

也是按二进制小数每一位的权重凑数，直接看

Repeated Multiplication by 2 乘2取整法

具体步骤：

1. 乘以2：将十进制小数的小数部分乘以2。
2. 取整数：取结果的整数部分（必然是0或1），这个整数就是二进制小数的第一位（最高位）。
3. 取小数：去掉结果的整数部分，将剩下的小数部分作为下一步的输入。
4. 重复：重复步骤1-3，直到小数部分变为0，或者达到所需的精度为止。
5. 排序：将每次取出的整数部分按顺序排列，就得到了二进制表示的小数部分。

注意

• 小数转换往往有截断误差，转换到所需的精度即可停止
• 题目可能会要求写出转成二进制循环小数的循环节
  • 观察每一次重复步骤中剩下小数部分的结果，当剩余的小数部分出现重复时，就代表开始循环了，一次重复内得到的所有整数部分就是循环节
  • 详见例2

例2：将十进制小数 0.7 转换为二进制（可能无限）

1. $0.7 \times 2 = 1.4$
   • 取整数部分：1
   • 剩下的小数部分：0.4
2. $0.4 \times 2 = 0.8$
   • 取整数部分：0
   • 剩下的小数部分：0.8
3. $0.8 \times 2 = 1.6$
   • 取整数部分：1
   • 剩下的小数部分：0.6
4. $0.6 \times 2 = 1.2$
   • 取整数部分：1
   • 剩下的小数部分：0.2
5. $0.2 \times 2 = 0.4$
   • 取整数部分：0
   • 剩下的小数部分：0.4 （注意：这里的小数部分0.4在第2步出现过，说明开始循环了）

既有整数又有小数

拆成整数和小数部分分别处理即可

Binary-to-Hexadecimal Conversion

• 四合一：二进制的4位一组合，转换成对应的一位16进制即可，巨快
• 最高位和最低位（头尾）不满4位的位置，补零即可

Hexadecimal-to-Binary Conversion

• 一拆四：一位16进制拆成对应的4位二进制即可
• 头尾多出的零省略掉

Hexadecimal-to-Decimal Conversion

• To convert a hexadecimal number to its decimal equivalent is to multiply the decimal value of each hexadecimal digit by its weight and take the sum of these products.
• 每一位乘以其权重，相加即可

Decimal-to-Hexadecimal Conversion

• 短除法可以直接解决
• Repeated division of a decimal number by 16 will produce the equivalent hexadecimal number, formed by the remainder of the divisions. The first remainder produced is the least significant digit (LSD). Each successive division by 16 yields a remainder that becomes a digit in the equivalent hexadecimal number.

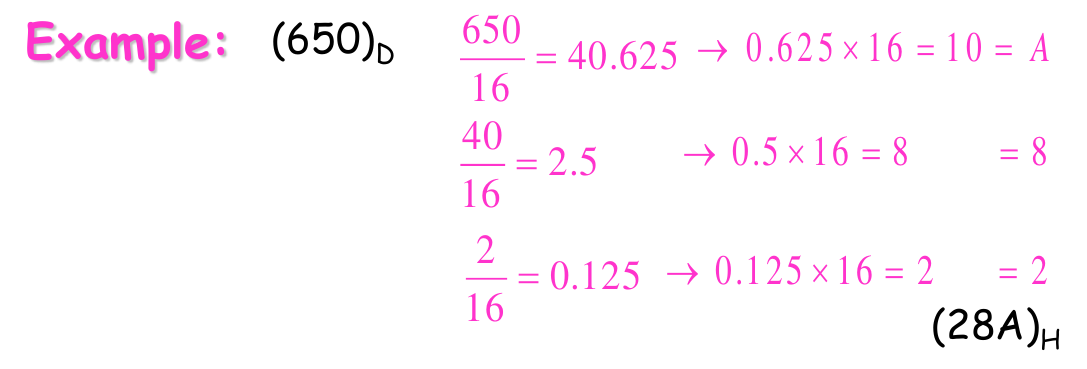
Binary Arithmetic

Binary Addition

The four basic rules for adding binary digits (bits) are as follows:

• 0 + 0 = 0 Sum of 0 with a carry of 0
• 0 + 1 = 1 Sum of 1 with a carry of 0
• 1 + 0 = 1 Sum of 1 with a carry of 0
• 1 + 1 = 10 Sum of 0 with a carry of 1

Binary Addition with a carry

• 1 + 0 + 0 = 01 Sum of 1 with a carry of 0
• 1 + 0 + 1 = 10 Sum of 0 with a carry of 1
• 1 + 1 + 0 = 10 Sum of 0 with a carry of 1
• 1 + 1 + 1 = 11 Sum of 1 with a carry of 1

Binary Subtraction

• The four basic rules for subtracting bits are as follows:
• The fourth rule shows a borrow from the next column to the left. A borrow is required when subtracting a 1 from a 0.
  • 0 - 0 = 0
  • 1 - 1 = 0
  • 1 - 0 = 1
  • (1)0 - 1 = 1 0 - 1 with a borrow of 1

Binary Multiplication

• The four basic rules for multiplying bits are as follows:
  • 0 × 0 = 0
  • 0 × 1 = 0
  • 1 × 0 = 0
  • 1 × 1 = 1
• Multiplication is performed with binary numbers in the same manner as with decimal numbers. It involves forming partial products, shifting each successive partial product left one place, and then adding all the partial products.

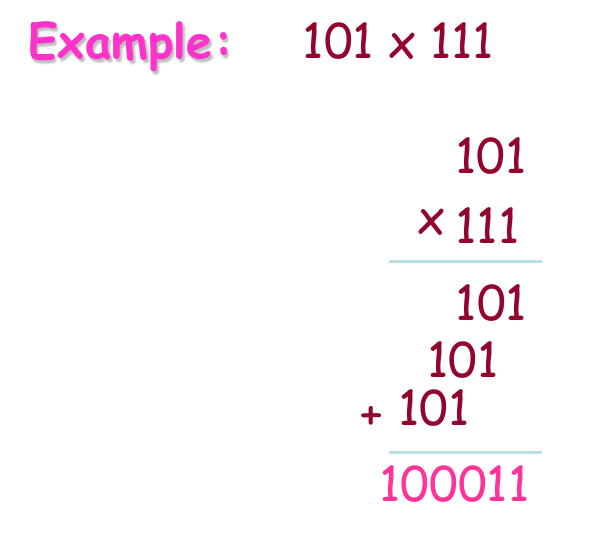
Binary Division

Division in binary follows the same procedure as division in decimal.

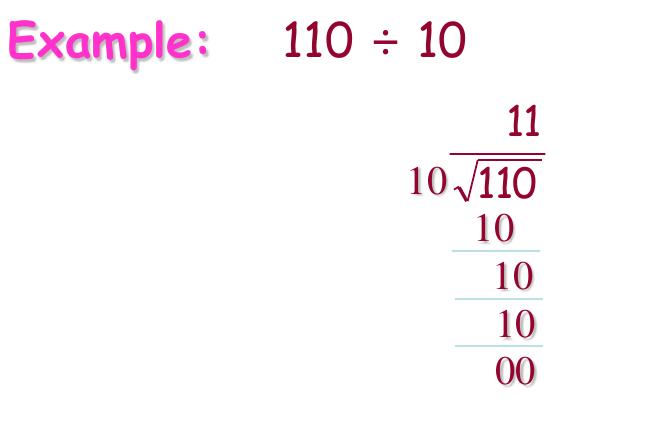
Signed Numbers and Arithmetic Operations

Sign-Magnitude System 原码

The sign bit: 符号位 the left-most bit in a signed binary number.

• A 0 is for positive, and a 1 is for negative.
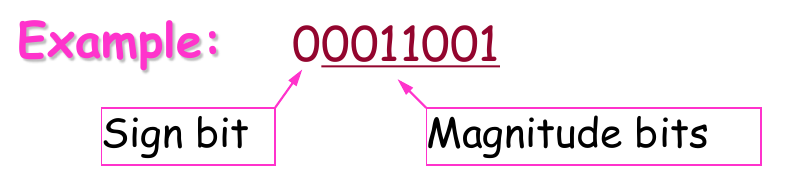
• When a signed binary number is represented in sign-magnitude, the left-most bit is the sign bit and the remaining bits are the magnitude bits.
• The magnitude bits are in true (un-complemented) binary for both positive and negative numbers.
  • In the sign-magnitude system, a negative number has the same magnitude bits as the corresponding positive number but the sign bit is a 1 rather than a zero.
• 人话：数值位就是正常的二进制，符号位确定符号

Decimal Values of signed numbers

• The decimal values of positive and negative numbers in the sign-magnitude system are determined by summing the weights in all the magnitude bit positions where there are 1s and ignoring those positions where there are zeros.
• 人话：数值位就是正常的二进制数转十进制，符号位确定符号

1’s Complement System 反码

• Positive numbers in the 1’s complement system are represented the same way as the positive sign-magnitude numbers.
• Negative numbers, however, are the 1’s complements of the corresponding positive numbers.
• 人话：
  • 对于正数，反码与原码一致。
  • 对于负数，原码的数值位按位取反得反码。符号位不变。

2’s Complement System 补码

• 人话：
  • 对于正数，补码与原码一致。
  • 对于负数，反码的数值位+1得到补码。符号位不变。
• 原码转补码：
  • 对于正数，不变
  • 对于负数，原码的数值位按位取反+1得到补码
• 补码转原码：
  • 对于正数，不变
  • 对于负数，补码转回原码，需要将数值位-1后再取反（注意顺序，不要反了！）

Arithmetic Operation with Signed Numbers

• 带符号加减法都使用2’s Complement System 补码进行运算

Addition

• 就是把补码当作二进制数相加即可
  • 结果如果符号位是0（$\text{sum} \geq 0$），那么结果就是这个二进制数
  • 结果如果符号位是1（$\text{sum} < 0$），那么结果是二进制数的补码表示
• Discard any carry bit 扔掉进位

溢出情况

• 正数+正数 或 负数+负数可能会溢出
• 溢出的表现为符号位错误，例如
  • 符号位出现0+0=1
  • 符号位出现1+1=0

Subtraction

• Subtraction is a special case of addition. The subtraction operation changes the sign of the subtrahend（减数） and adds it to the minuend（被减数）. The result of a subtraction is called the difference.
• Subtraction: to subtract two signed number
  • changes the sign of the subtrahend, take the 2’s complement of the subtrahend and add
  • Discard any final carry bit 扔掉进位
• 人话：转化成有符号数加法操作

Multiplication

• 乘除法的核心都是符号位单独处理（异或）+数值位做无符号运算
• 乘法：提取符号位，结果的符号位为乘数和被乘数符号位的异或。数值位做无符号乘法
  • 无符号乘法和在十进制里面学的差不多，也是算出所有的部分积，然后相加

Division

• 除法：提取符号位，结果的符号位为除数和被除数符号位的异或。数值位做无符号除法
  • 列个除法式子算无符号除法
• PPT给的是重复尝试减法，实际上这样的效率极低，不可能这样算的

Binary Coded Decimal BCD码

• 常识，直接跳过

BCD码加法

• 先进行普通的二进制加法，然后对每个超过9的4-bit sum进行调整
• 考试考到，如果不要求过程，建议直接转成十进制算完再转回BCD，因为人算十进制加法和BCD转换比二机制加法+调整快多了！

Gray Code/Reflected Binary Code 格雷码/RBC码

格雷码的定义

• 格雷码，又称循环二进制码或反射二进制码（Reflected Binary Code, RBC），是一种二进制数字系统。它的主要特点是：任意两个连续的数值之间，只有一位（bit）会发生变化。
  • 这个特性与普通的标准二进制码不同。在标准二进制码中，从一个数变到下一个数时，可能会有多位同时改变（例如，从 3 的二进制 011 变到 4 的二进制 100，有三位都变了）。
• 格雷码的这个“单位距离”特性使得它在某些应用中非常有用，特别是在减少数字系统（如机械编码器或数字通信）中状态转换时可能产生的错误。因为只有一个比特位变化，所以转换期间的中间状态（如果读取不及时）不会导致大的数值跳跃错误。

格雷码与普通二进制数的互转

以下是如何在格雷码和标准二进制码之间进行转换：

1. 二进制转格雷码

   • 最高位 (MSB)： 格雷码的最高位与二进制码的最高位相同。
   • 其他位： 从左到右（从次高位开始），格雷码的每一位等于对应二进制位与其左边一位（即更高一位）的二进制位进行 异或 (XOR, $\oplus$) 运算的结果。
   • 公式描述（从左到右，第 $n$ 位是最高位）：
     • $g_n = b_n$
     • $g_i = b_i \oplus b_{i+1}$ （对于 $i = n-1, n-2, ..., 1, 0$）
   • 举例： 将二进制数 1011 转换为格雷码。
     • 最高位：$g_3 = b_3 = 1$
     • 次高位：$g_2 = b_2 \oplus b_3 = 0 \oplus 1 = 1$
     • 次低位：$g_1 = b_1 \oplus b_2 = 1 \oplus 0 = 1$
     • 最低位：$g_0 = b_0 \oplus b_1 = 1 \oplus 1 = 0$
     • 所以，二进制 1011 对应的格雷码是 1110。

2. 格雷码转二进制码

   • 最高位 (MSB)： 二进制码的最高位与格雷码的最高位相同。
   • 其他位： 从左到右（从次高位开始），二进制码的每一位等于对应格雷码位与其左边一位（即更高一位）的 已计算出的二进制位 进行 异或 (XOR, $\oplus$) 运算的结果。
   • 公式描述（从左到右，第 $n$ 位是最高位）：
     • $b_n = g_n$
     • $b_i = g_i \oplus b_{i+1}$ （对于 $i = n-1, n-2, ..., 1, 0$） 注意这里的 $b_{i+1}$ 是已经算出来的二进制位
   • 举例： 将格雷码 1110 转换为二进制数。
     • 最高位：$b_3 = g_3 = 1$
     • 次高位：$b_2 = g_2 \oplus b_3 = 1 \oplus 1 = 0$ （这里的 $b_3$ 是上一步算出的二进制最高位）
     • 次低位：$b_1 = g_1 \oplus b_2 = 1 \oplus 0 = 1$ （这里的 $b_2$ 是上一步算出的二进制次高位）
     • 最低位：$b_0 = g_0 \oplus b_1 = 0 \oplus 1 = 1$ （这里的 $b_1$ 是上一步算出的二进制次低位）
     • 所以，格雷码 1110 对应的二进制数是 1011。