Rookie's blog

Chapter3 Logic Gates

Chapter3 Logic Gates

基本逻辑门

1. 与门 (AND Gate)

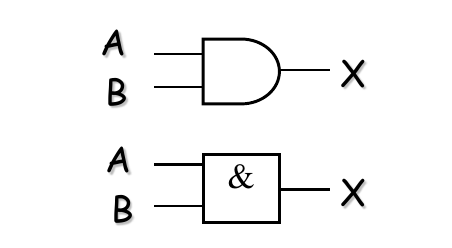
image-20250505202018491
  • 逻辑功能: 当所有输入都为高电平（1）时，输出才为高电平（1）；否则输出为低电平（0）。
  • 布尔表达式: 对于两个输入 A 和 B，输出 Q 可以表示为：Q=A⋅BQ = A \cdot B 或 Q=ABQ = AB
  • 真值表:
    输入 A 输入 B 输出 Q (A · B)
    0 0 0
    0 1 0
    1 0 0
    1 1 1

2. 或门 (OR Gate)

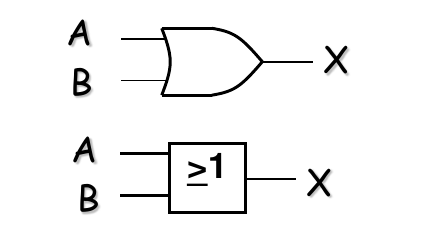
image-20250505202036424
  • 逻辑功能: 当至少一个输入为高电平（1）时，输出就为高电平（1）；只有所有输入都为低电平（0）时，输出才为低电平（0）。
  • 布尔表达式: 对于两个输入 A 和 B，输出 Q 可以表示为：
    Q=A+BQ = A + B
  • 真值表:
    输入 A 输入 B 输出 Q (A + B)
    0 0 0
    0 1 1
    1 0 1
    1 1 1

3. 非门 (NOT Gate / Inverter)

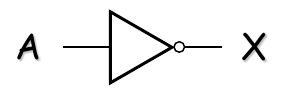
image-20250505202005726
  • 逻辑功能: 输出与输入的状态相反。如果输入为高电平（1），输出为低电平（0）；如果输入为低电平（0），输出为高电平（1）。非门只有一个输入。
  • 布尔表达式: 对于输入 A，输出 Q 可以表示为：Q=A‾Q = \overline{A} 或 Q=A′Q = A'
  • 真值表:
    输入 A 输出 Q (A‾\overline{A})
    0 1
    1 0

扩展逻辑门

4. 与非门 (NAND Gate)

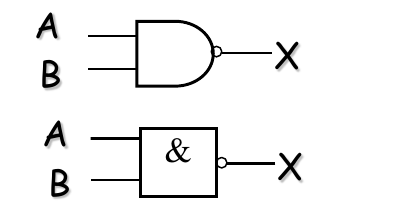
image-20250505202208167
  • 逻辑功能: 相当于与门（AND）后面接一个非门（NOT）。只有当所有输入都为高电平（1）时，输出才为低电平（0）；否则输出为高电平（1）。NAND 门是一种“通用”逻辑门，因为可以用它组合出其他所有逻辑门。
  • 布尔表达式: 对于两个输入 A 和 B，输出 Q 可以表示为：Q=A⋅B‾Q = \overline{A \cdot B} 或 Q=AB‾Q = \overline{AB}
  • 真值表:
    输入 A 输入 B 输出 Q (A⋅B‾\overline{A \cdot B})
    0 0 1
    0 1 1
    1 0 1
    1 1 0

5. 或非门 (NOR Gate)

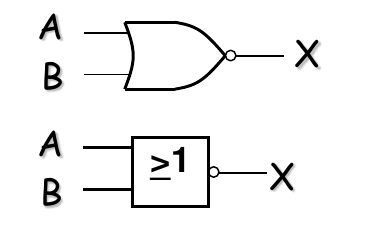
image-20250505202221403
  • 逻辑功能: 相当于或门（OR）后面接一个非门（NOT）。只有当所有输入都为低电平（0）时，输出才为高电平（1）；否则输出为低电平（0）。NOR 门也是一种“通用”逻辑门。
  • 布尔表达式: 对于两个输入 A 和 B，输出 Q 可以表示为：Q=A+B‾Q = \overline{A + B} 或 Q=A‾⋅B‾Q = \overline{A} \cdot \overline{B}
  • 真值表:
    输入 A 输入 B 输出 Q (A+B‾\overline{A + B})
    0 0 1
    0 1 0
    1 0 0
    1 1 0

6. 异或门 (XOR Gate - Exclusive OR)

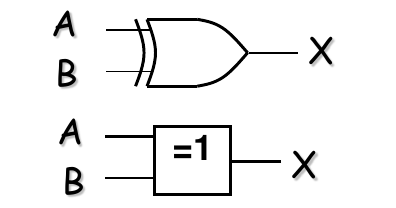
image-20250505202238647
  • 逻辑功能: 当两个输入不相同时（一个为 1，一个为 0），输出为高电平（1）；当两个输入相同时（都为 0 或都为 1），输出为低电平（0）。常用于实现加法器、奇偶校验等。
  • 布尔表达式: 对于两个输入 A 和 B，输出 Q 可以表示为：Q=A⊕BQ = A \oplus B 或 Q=AB‾+A‾BQ = A\overline{B} + \overline{A}B
  • 真值表:
    输入 A 输入 B 输出 Q (A⊕BA \oplus B)
    0 0 0
    0 1 1
    1 0 1
    1 1 0

7. 同或门 (XNOR Gate - Exclusive NOR)

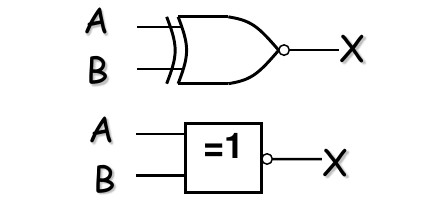
image-20250505202253087
  • 逻辑功能: 相当于异或门（XOR）后面接一个非门（NOT）。当两个输入相同时（都为 0 或都为 1），输出为高电平（1）；当两个输入不相同时（一个为 1，一个为 0），输出为低电平（0）。也称为等价门（Equivalence Gate），常用于比较两个比特是否相等。
  • 布尔表达式: 对于两个输入 A 和 B，输出 Q 可以表示为：Q=A⊕B‾Q = \overline{A \oplus B} 或 Q=AB+A‾⋅B‾Q = A B + \overline{A}\cdot\overline{B}
  • 真值表:
    输入 A 输入 B 输出 Q (A⊕B‾\overline{A \oplus B})
    0 0 1
    0 1 0
    1 0 0
    1 1 1
0%