Chapter4 Boolean Algebra & Logical Simplification

Boolean Operations and Expressions

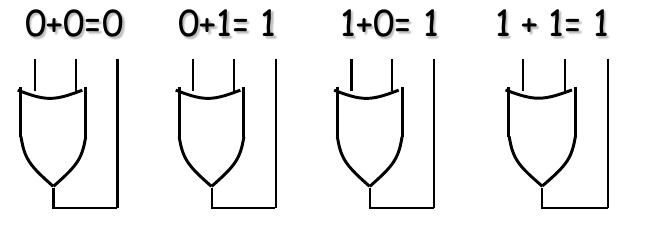
• Boolean addition is equivalent to the OR operation and the basic rules are illustrated with their relation to the OR gates as follows:
  • A sum term is equal to 1 when one or more of the literals in the term are 1.
  • A sum term is equal to 0 only if each of the literals is 0.

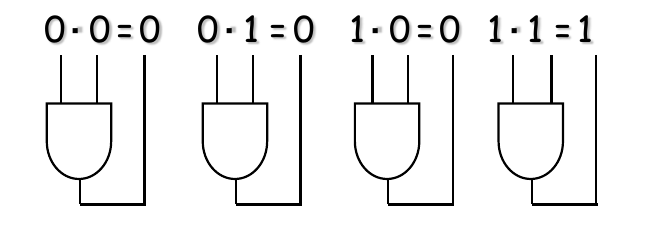
• Boolean multiplication is equivalent to the AND operation and the basic rules are illustrated with their relation to the AND gates as follows:

  • A product term is equal to 1 only if each of the literals in the term are 1.
  • A product term is equal to 0 when one or more of the literals is 0.
  

Laws and Rules of Boolean Algebra

Commutative, Associative and Distributive Law

序号	定律 (Laws)	布尔表达式 (Boolean Expression)
1	Commutative law of addition 加法交换律	$A + B = B + A$
1	Commutative law of multiplication 乘法交换律	$A·B = B·A$
2	Associative law of addition 加法结合律	$A+(B+C)=(A+B)+C$
2	Associative law of multiplication 乘法结合律	$A·(B·C) = (A·B)·C$
3	Distributive law 分配律	$A·(B+C) = A·B+A·C$

常用运算公式

1. $A + 0 = A$

2. $A + 1 = 1$

3. $A \cdot 0 = 0$

4. $A \cdot 1 = A$

5. $A + A = A$

6. $A + \overline{A} = 1$

7. $A \cdot A = A$

8. $A \cdot \overline{A} = 0$

9. $\overline{\overline{A}} = A$

10. $A + AB = A$

11. $A + \overline{A}B = A + B$

12. $(A + B)(A+C) = A+BC$

13. $AB + \overline{A}C + BC = AB + \overline{A}C$

14. $\overline{A \cdot B} = \overline{A} + \overline{B}$

15. $\overline{A + B} = \overline{A} \cdot \overline{B}$

Boolean Analysis of a logic Circuit

Constrcting the truth table for a logic circuit

1. 先判断表有几行，大概长什么样（n个输入就有$2^n$种情况）
2. 建议使用逻辑判断的方法把输出为0/1的输入（选简单的算）一步步找出来
3. 表达式比较复杂，逻辑判断不方便的话，那就老老实实一个个算！

Standard Forms of Boolean Expressions

1. Sum-of-Products Form (SOP Form)
2. Product-of-Sums Form (POS Form)
3. Standard SOP Form
4. Standard POS Form

Conversion of a General Expression to SOP Form

• Any logic expression can be changed into SOP form by applying Boolean algebra techniques.
• 使用下面这个式子，把积项中所有缺失的项全部补出来（拆出来）

$$1 = X + \overline{X}$$

Some Concepts

• Normal Product Term: Product term with no repeated variables.
• Minterm over N Variables: Normal product term with N variables

The Standard SOP Form

• Standard SOP Form: Sum of min-terms Form

Converting Product Terms to Standard SOP

1. 识别缺失变量：对于一个非标准的积项，确定表达式域中哪些变量是缺失的。
2. 乘以包含缺失变量的和项：将该非标准积项乘以一个由“缺失变量 + 其补数”构成的和项（例如，如果变量 ‘D’ 缺失，则乘以 $(D+\overline{D})$）。根据布尔代数规则 $A + \overline{A} = 1$，这样做不会改变积项的逻辑值。应用分配律后，这将产生两个新的积项。
3. 重复：对新产生的积项，重复步骤1和2，处理任何仍然缺失的变量，直到所有得到的积项都包含域中的所有变量（以原变量或补数形式出现）。

Binary Representation of a Standard Product Term

• A Standard Product term is equal to 1 for only one combination of variable values.

$$A\overline{B}C\overline{D} = 1 \cdot \overline{0} \cdot 1 \cdot \overline{0} = 1 \cdot 1 \cdot 1 \cdot 1 = 1$$

• So the product term has a binary value of 1010, $(10)_D$
• For minterm: 1 is variable, 0 is complement
• An SOP expression is equal to 1 only if one or more of the product terms in the expression is equal to 1.

POS Form

• Sum Term: A single literal or a sum (OR) of 2 or more literals.
• Product of Sums: Logical product of sum terms.
• Normal Sum Term: Sum term with no repeated variables.
• Maxterm over N variables: Normal sum term with N variables

The Standard POS Form

• Standard POS Form is Product of Maxterms Form

Conversion of a Sum Term to Standard POS

1. 识别缺失变量：对于一个非标准的和项，确定表达式域中哪些变量是缺失的。
2. 添加缺失变量的积项：在非标准的和项中，加上一个由缺失变量及其补数组成的积项（例如，如果变量 $D$ 缺失，则加上 $D\overline{D}$）。根据布尔代数规则 $A \cdot \overline{A} = 0$，添加这个积项不会改变和项的逻辑值。
3. 应用分配律：使用布尔代数规则 $A+BC = (A+B)(A+C)$ 来分解表达式，得到两个和项。
4. 重复：对新产生的和项，重复步骤1-3，处理任何仍然缺失的变量，直到每个和项都包含域中的所有变量（以原变量或补数形式出现）。

Binary Representation of a Standard Sum Term

• 一个标准和项（也称为 Maxterm，最大项）只在唯一一种变量取值组合下等于 $0$。
• 其二进制表示的规则是：
  • 变量的原形式（如 $A$）对应二进制值 $0$。
  • 变量的补数形式（如 $\overline{B}$）对应二进制值 $1$。
• 例如，标准和项 $A+\overline{B}+C+\overline{D}$ 对应的二进制值是 $0101$。当输入变量为 $A=0, B=1, C=0, D=1$ 时，该和项的值为 $0+\overline{1}+0+\overline{1} = 0+0+0+0 = 0$。
• 一个标准的和之积（POS）表达式，只要其包含的任何一个标准和项等于 $0$，整个表达式的值就为 $0$。

Conversion Between Different Forms

Convertincg Standard SOP to Standard POS

• SOP和POS，即最大项和最小项是互补的

  • 利用这一点进行计算
  • SOP中的最大项和POS中的最小项

• The binary values of the product terms in a given standard SOP expression are not present in the equivalent standard POS expression.

• Also, the binary values that are not represented in the SOP expression are present in the equivalent POS expression.

So, the steps are:

1. Evaluate each product term in the SOP expression. That is, determine the binary numbers which represent the product terms.

2. Determine all of the binary numbers not included in the evaluation in step 1

3. Write the equivalent sum term for each binary number from step 2 and express in POS form.

   • For minterm: 1 is variable, 0 is complement

   • For maxterm: 1 is complement, 0 is variable

Logic function Simplification

没啥好写的，灵活应用前面说的公式，将表达式尽可能化到最简

卡诺图(The Karnaugh Map)

• 定义与用途: 卡诺图（Karnaugh Map）是一种图形化的方法，用于简化布尔表达式。它利用人脑的模式识别能力来寻找最简化的逻辑表达式。卡诺图类似于真值表，展示所有可能的输入变量组合及其对应的输出。
• 结构: 卡诺图是一个单元格阵列，每个单元格对应一个输入变量组合。单元格的排列遵循格雷码顺序，使得相邻单元格之间只有一个变量发生变化。
• 相邻性:
  • 物理上相邻（上下左右）的单元格是相邻的。
  • 顶行与底行对应的单元格相邻。
  • 最左列与最右列对应的单元格相邻。
• 变量数量: 卡诺图对于简化最多六个变量的表达式非常有效。对于更多变量，模式识别会变得困难。常见的有 2 变量、3 变量、4 变量和 5 变量卡诺图。

2-5变量卡诺图基本形式

2变量

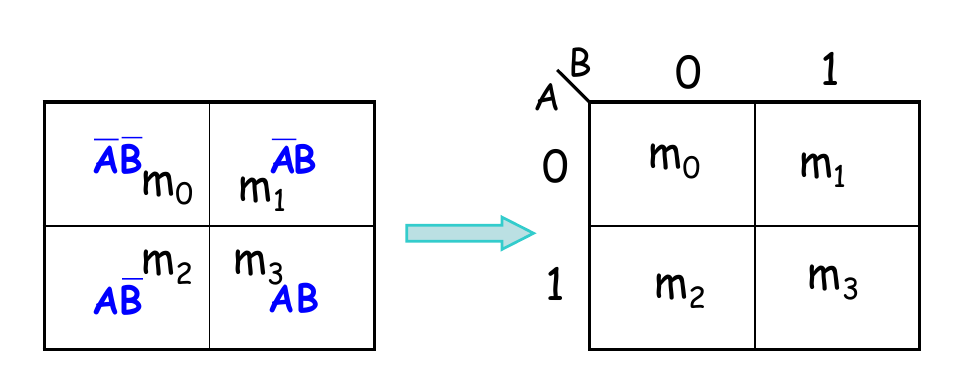
3变量

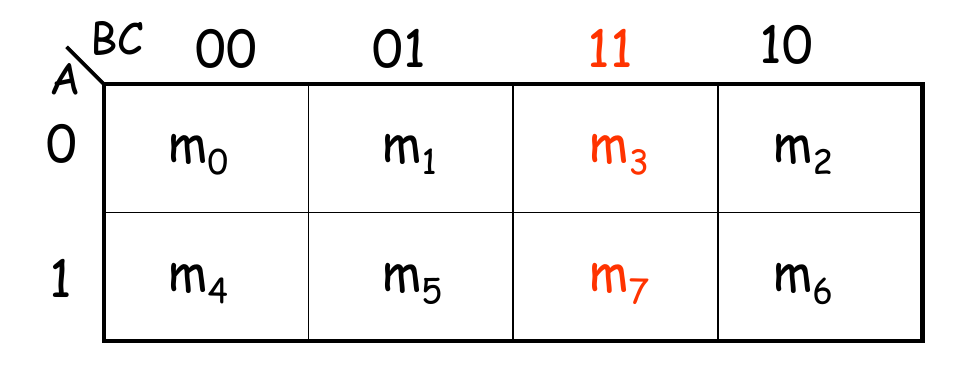
4变量

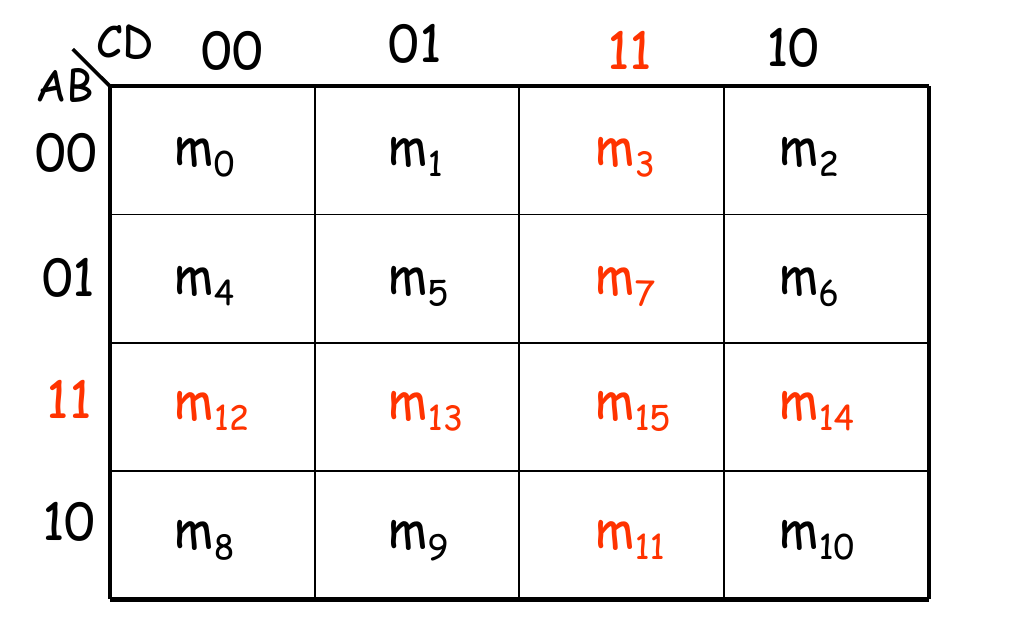
5变量

5变量卡诺图有两种形式，注意：这两种形式在看相邻单元格时的方法是不同的

1. 上面这种用C=0/1分左右的卡诺图，看相邻项的时候沿着中间这条红线把纸面对折（或者也可以说，右面以中心红线为轴翻转180），左右两部分叠在一起，上下相邻的单元格是相邻的

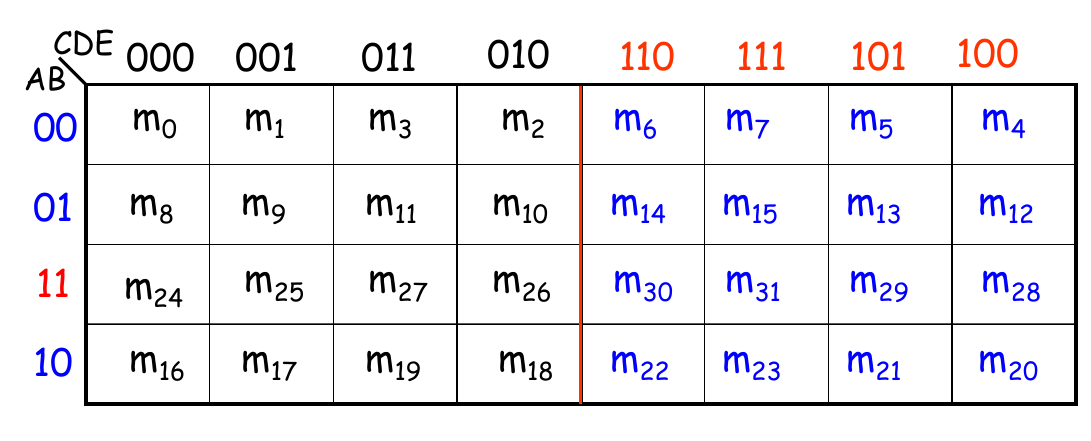
2. 下面这种用A=0/1分左右的卡诺图，看相邻项的时候把左右两部分直接上下重叠即可（单元格相互对应），不要翻转

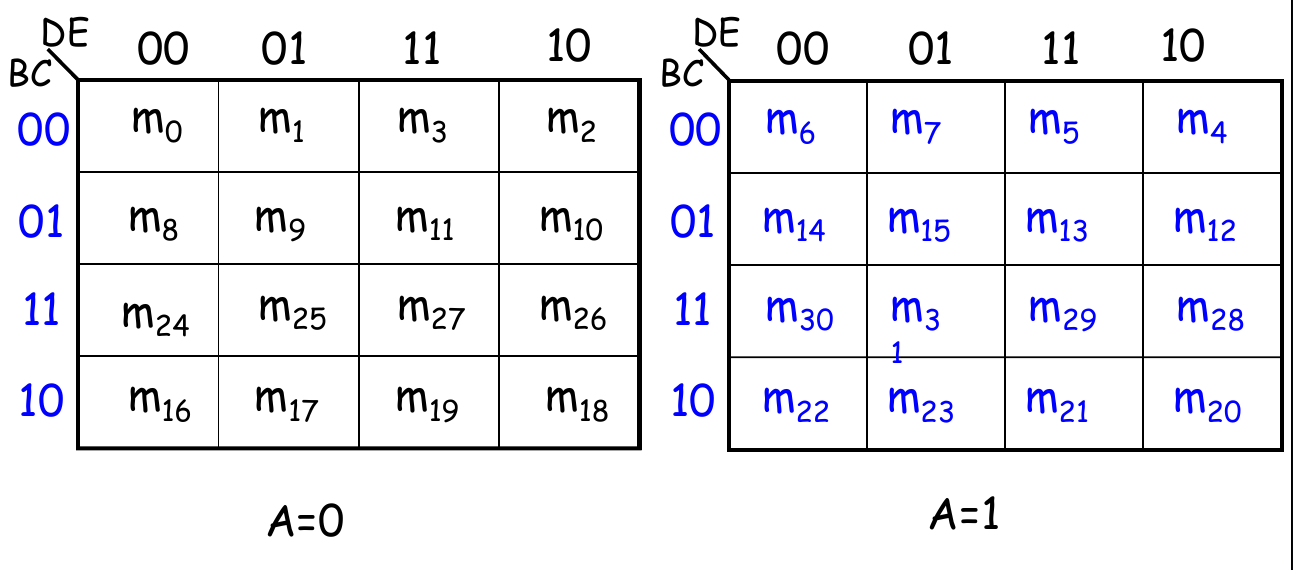
使用卡诺图进行逻辑简化 (SOP - 积之和)

1. 映射标准 SOP 表达式:
   • 确定标准 SOP 表达式中每个乘积项的二进制值。
   • 在卡诺图上对应二进制值的单元格中标注 1。地图上 1 的数量等于标准 SOP 表达式中乘积项的数量。未标注 1 的单元格对应表达式值为 0 的情况 [cite: 35]。
2. 映射非标准 SOP 表达式: 将非标准的 SOP 表达式的每个项扩展（补全缺失变量），然后在卡诺图上标记所有对应的单元格为 1。
3. 寻找最大分组 (Grouping):
   • 目标是最大化分组的大小并最小化分组的数量。
   • 分组必须包含 1, 2, 4, 8 或 16 个单元格。
   • 组内的每个单元格必须与同组的至少一个其他单元格相邻。
   • 尽可能圈出最大的分组 [cite: 46]。
   • 确保地图上所有的 1 都至少被一个分组包含。不允许 L 型或 U 型分组。
4. 确定最小项:
   • 对于每个分组，找出在分组内保持不变的变量。那些在组内既有原变量又有反变量形式出现的变量将被消去。
   • 根据分组大小确定最小乘积项 [cite: 51]：
     • 1 单元格组 -> n 变量乘积项 (n 为总变量数)
     • 2 单元格组 -> (n-1) 变量乘积项
     • 4 单元格组 -> (n-2) 变量乘积项
     • 8 单元格组 -> (n-3) 变量乘积项
5. 求和: 将所有分组对应的最小乘积项相加（逻辑或），得到最简 SOP 表达式。

使用卡诺图进行逻辑简化 (POS - 和之积)

• 映射标准 POS 表达式:
  • 确定标准 POS 表达式中每个和项的二进制值（使该和项为 0 的值）。
  • 在卡诺图上对应二进制值的单元格中标注 0。
• 分组与简化:
  • 过程与 SOP 类似，但是是分组 0 而不是 1。
  • 目标是圈出包含 1, 2, 4, 8 或 16 个 0 的最大分组。
  • 为每个分组确定最小和项（找出组内保持不变的变量，取反变量形式则保留反变量，取原变量形式则保留原变量，然后相加）。
  • 将所有分组对应的最小和项相乘（逻辑与），得到最简 POS 表达式。

无关项 (Don’t Care Terms)

• 定义: 输入变量的一种组合，其对应的输出可以是 0 也可以是 1。通常出现在某些输入组合不可能发生，或者发生了但我们不关心其输出值的场合。
• 应用: 在卡诺图上用 ‘X’ 标记。进行分组时，可以将 ‘X’ 视作 1（简化 SOP 时）或 0（简化 POS 时），以帮助形成更大的分组，从而得到更简化的表达式。