Chapter5 Combinatonal Logic

Chapter5 Combinatonal Logic 组合逻辑

5.1 Basic Combinational Logic

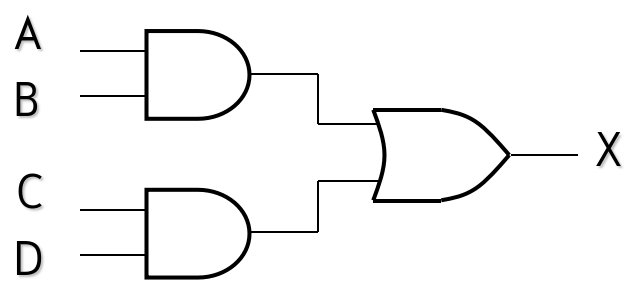
AND-OR Logic

An AND-OR circuit directly implements an SOP expression, assuming the complements (if any) of the variables are available.

AND-OR Invert Logic

When the output of an AND-OR circuit is complemented (inverted), it results in an AND-OR-Invert circuit.

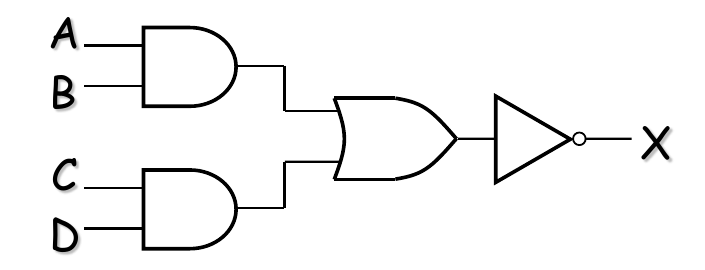$$ X = \overline{AB + CD} = (\overline{A} + \overline{B})(\overline{C} + \overline{D}) $$

Exclusive-OR (XOR) Logic

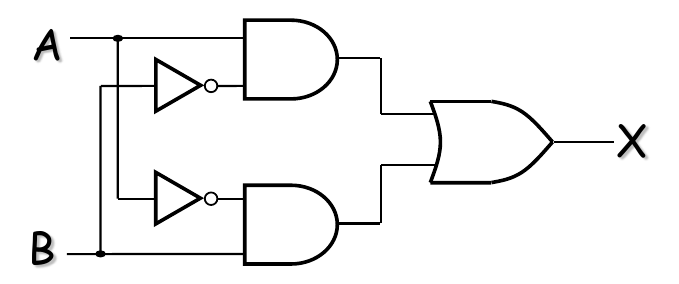$$ X = A \oplus B = A\overline{B} + \overline{A}B $$

Exclusive-NOR (XNOR) Logic

$$X = \overline{A \oplus B} = A B + \overline{A}\cdot\overline{B}$$

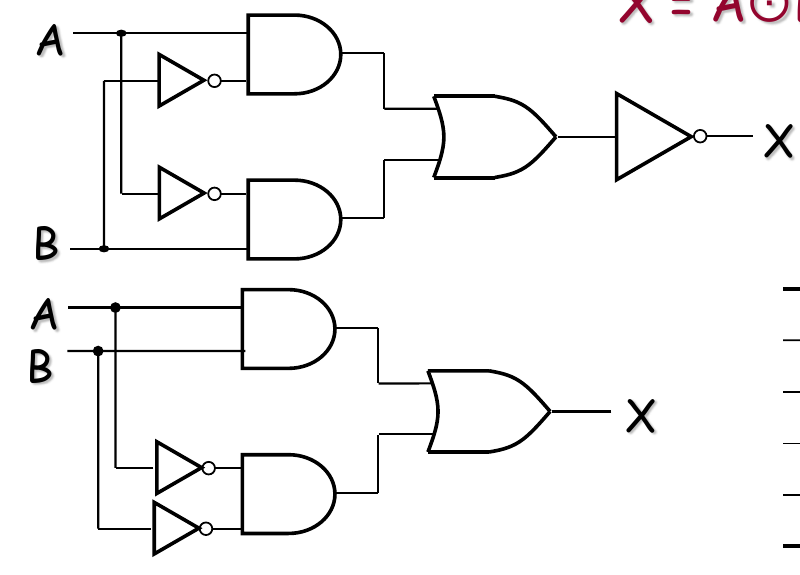
Implementing Combinational Logic

1. 会从逻辑表达式画逻辑电路图就行
2. 会从真值表画逻辑电路图就行
3. 就是些废话，跳过

The Universal Property of Extend Gates

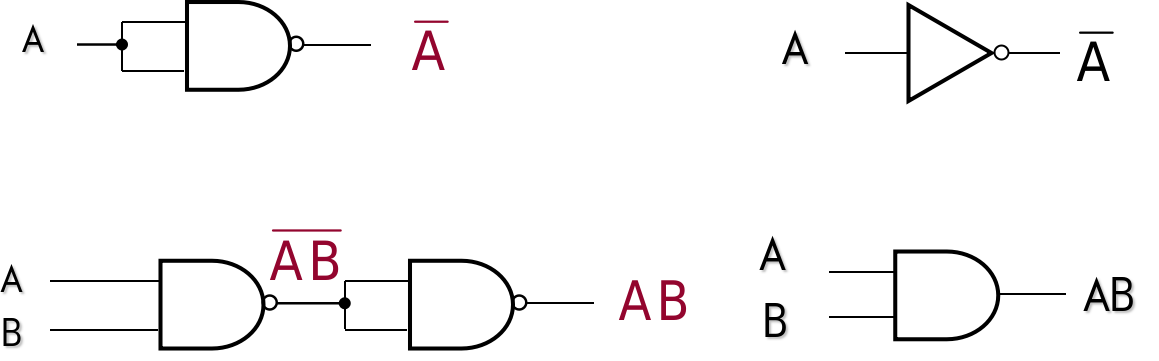
The NAND Gate as a Universal Logic Element

The NAND gate can be used to produce the NOT, AND, OR, and NOR operations.

The NAND gate used as an OR gate

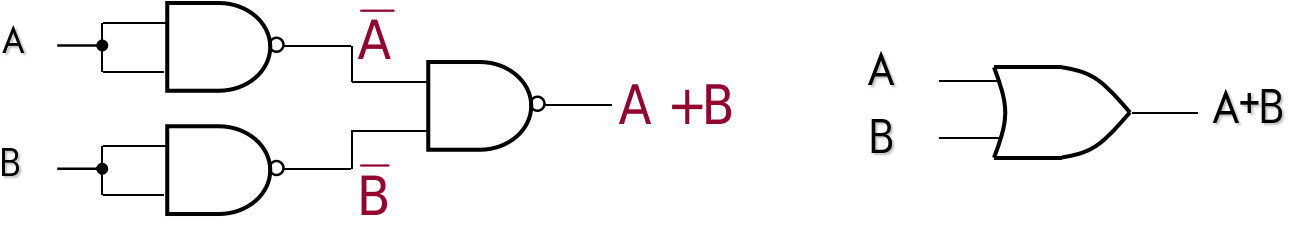
The NAND gate used as an NOR gate

The NOR Gate as a Universal Logic Element

The NOR gate can be used to produce the NOT, OR, AND, and NAND operations.

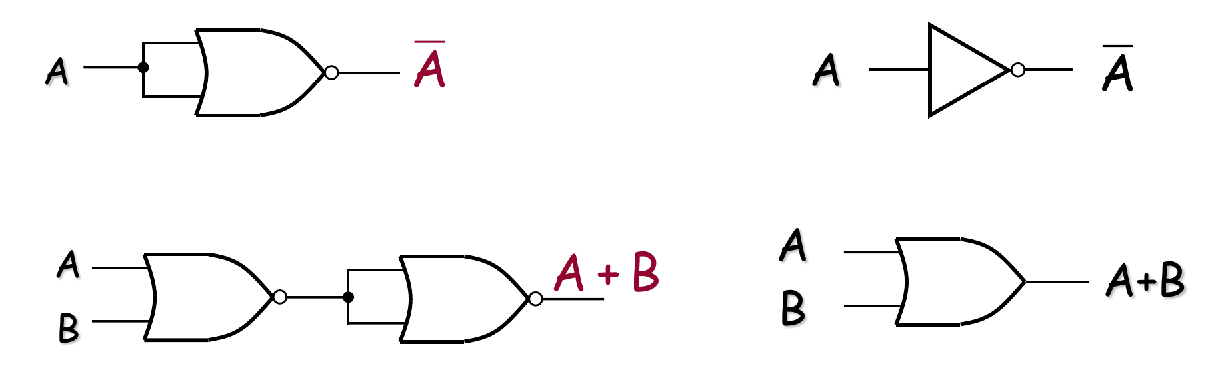
The NOR gate used as an AND gate

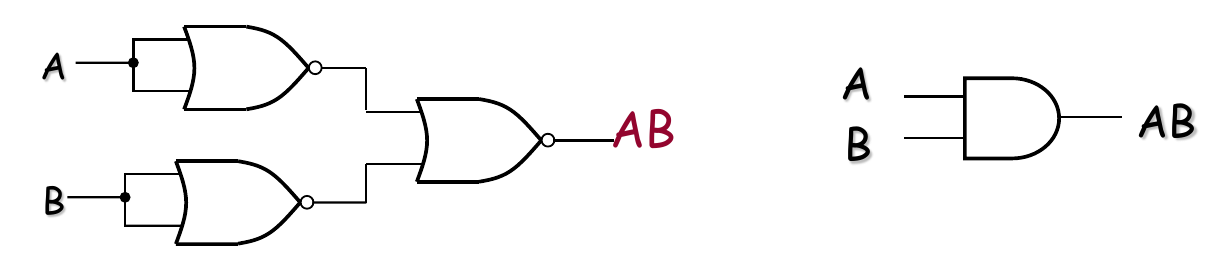
The NOR gate used as an NAND gate

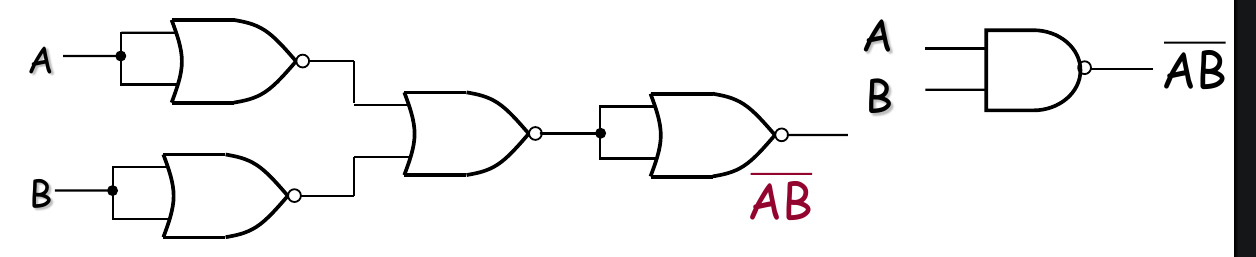
Combinational Logic Using Extend Gates

该部分要求

• 用前面给出的那些基本结构的组合来构建复杂逻辑就足够了
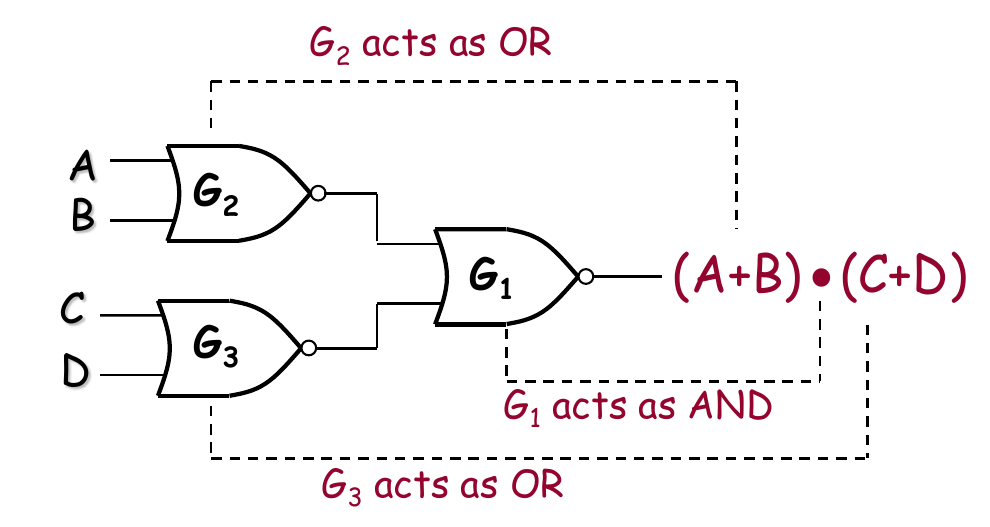
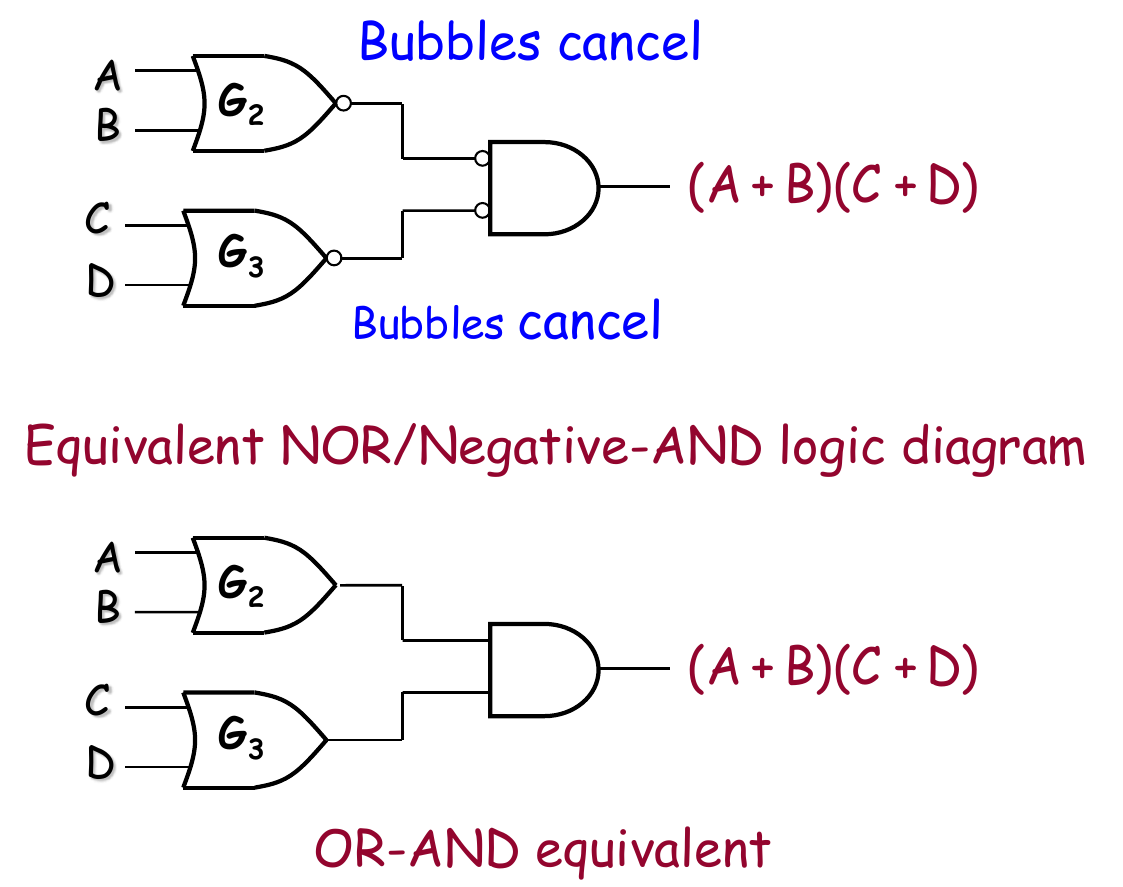
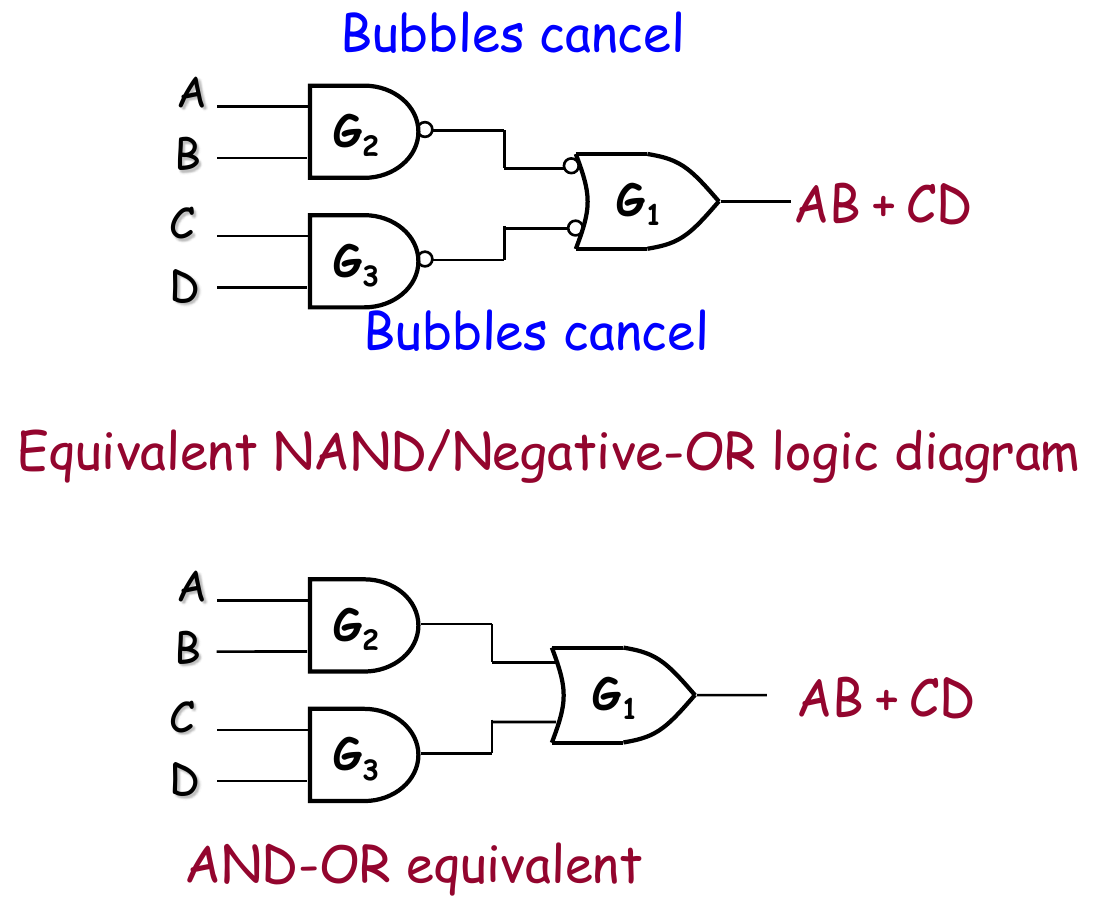
• 注意：分析这类逻辑电路时，有个技巧：Bubbles cancel
  • 两个圆圈表示两次取反，由于$\overline{\overline{A}} = A$，经过两次取反的信号就是原来的信号，相当于没变。分析的时候，为了简化复杂的电路，可以直接把成对的Bubble直接去掉。

两种常见的逻辑

NAND 实现 SOP 的逻辑

使用DeMorgan律 $\overline{AB} = \overline{A} + \overline{B}$

$$\begin{align} X = \overline{(\overline{AB})(\overline{CD})} = \overline{(\overline{A} + B)(\overline{C} + D)} = \overline{(\overline{A} + B)} + \overline{(\overline{C} + D)} = \overline{\overline{AB}} + \overline{\overline{CD}} = AB + CD \end{align}$$

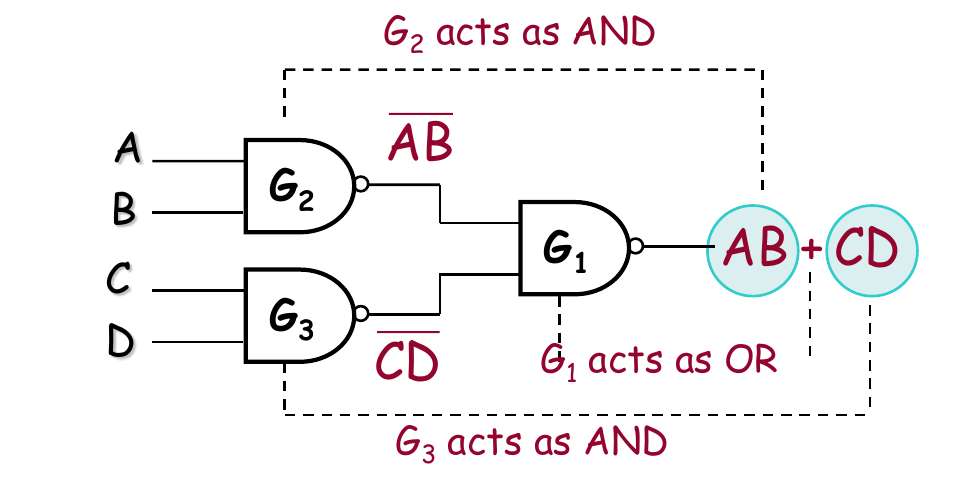
一种更高效的分析方法：

NOR 实现 POS 的逻辑

使用DeMorgan律 $\overline{A + B} = \overline{A} \cdot \overline{B}$

$$X = \overline{A + B + C + D} = \overline{(A + B)(C + D)} = (A + B)(C + D)$$