Chapter6 Functions of Combinational Logic

6.1 Adders

The Half Adder(半加器)

The half-adder accepts two binary digits on its inputs and produces two binary digits on outputs, a sum bit and a carry bit.

$\begin{cases} \sum = \overline{A}B + A\overline{B} = A \oplus B \\ C_{out} = AB \end{cases}$

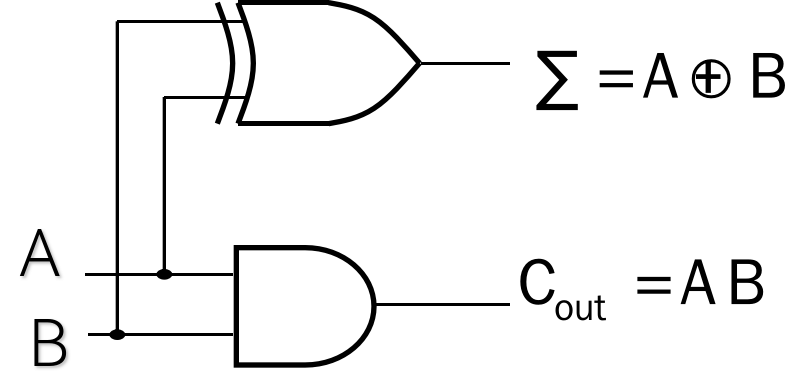
输入 A	输入 B	$\Sigma$ (Sum)	进位 (Carry)
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

The Full Adder(全加器)

The full-adder accepts two inputs and input carry and generates a sum output and an output carry.

使用逻辑门实现全加器

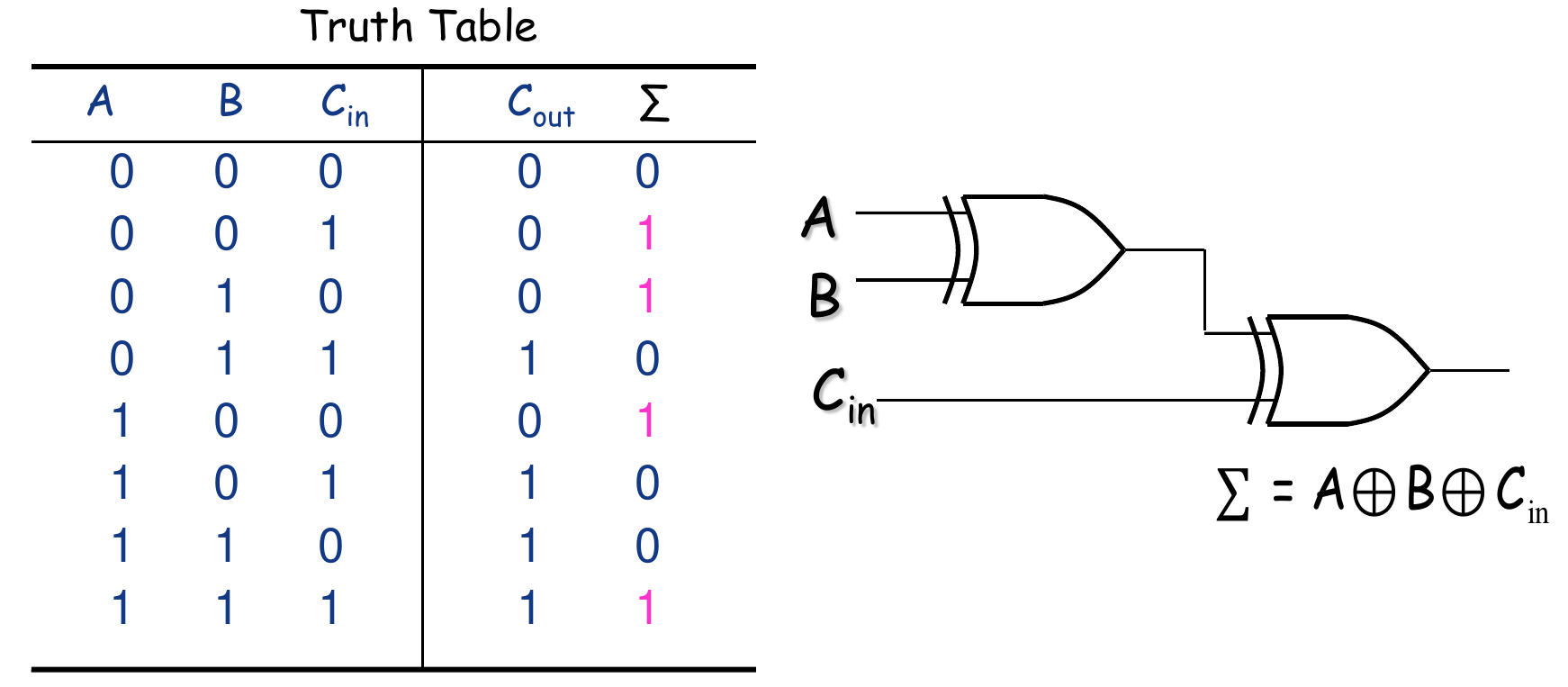$$ \begin{align} \sum &= \overline{A}BC_{in} + \overline{A}\overline{B}C_{in} + A\overline{B}\overline{C}_{in} + ABC_{in} \\ &= \overline{A}(BC_{in} + \overline{B}C_{in}) + A(\overline{B}\overline{C}_{in} + BC_{in}) \\ &= \overline{A}(B \oplus C_{in}) + A(\overline{B \oplus C_{in}}) = A\oplus B\oplus C_{in} \end{align} $$

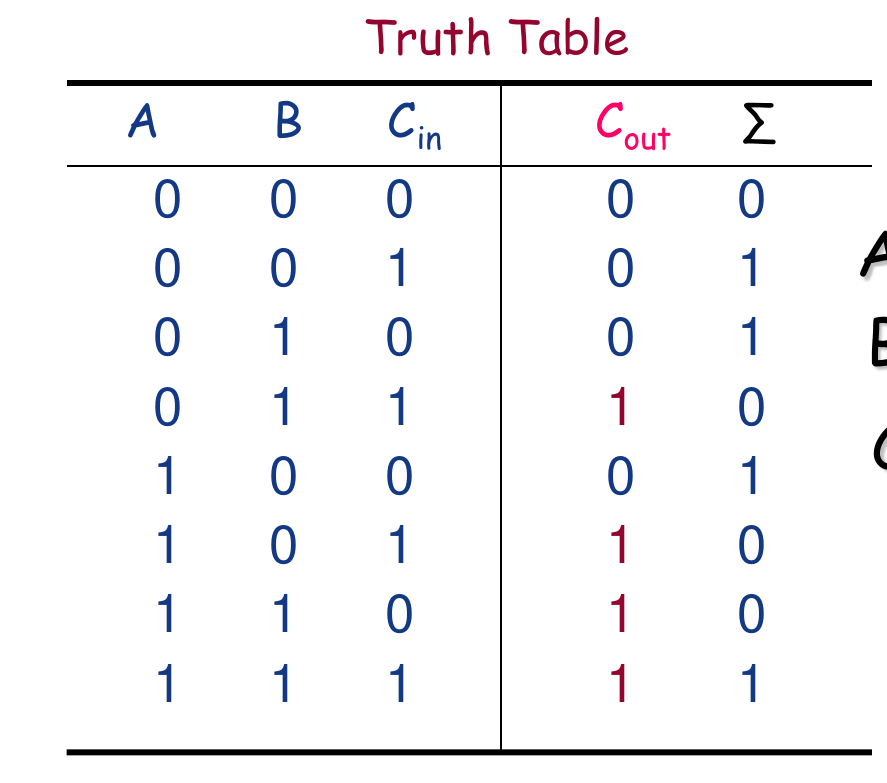
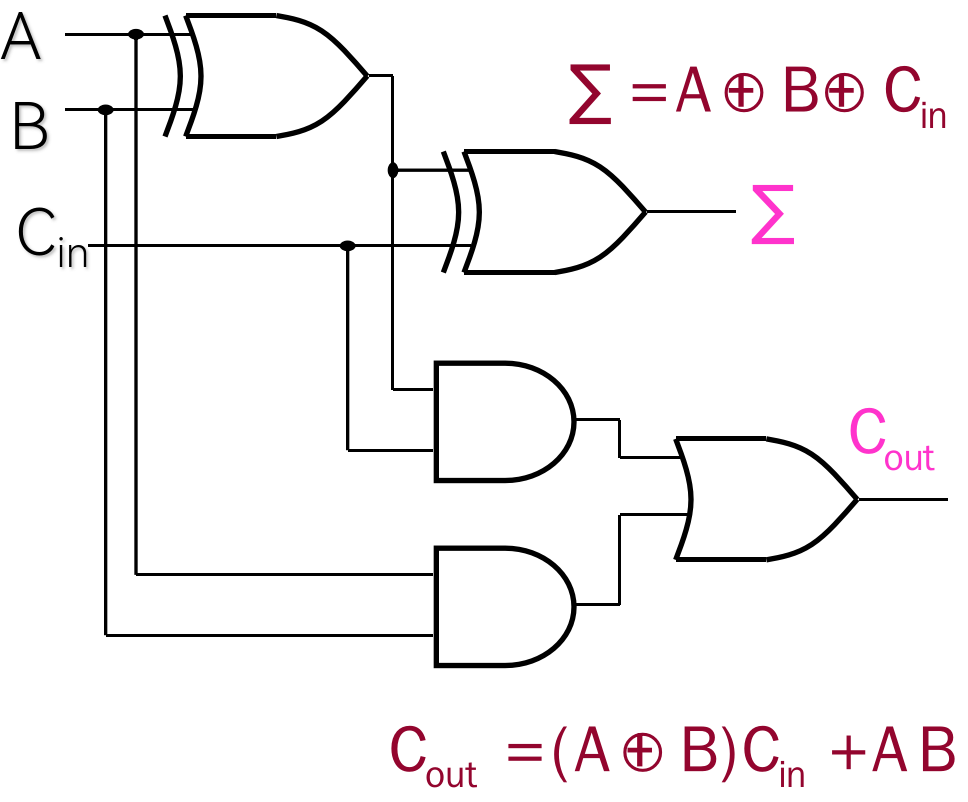$$ C_{out} = \overline{A}BC_{in} + A\overline{B}C_{in} + A\overline{B}\overline{C}_{in} + ABC_{in} = (\overline{A}B + A\overline{B})C_{in} + AB = (A \oplus B)C_{in} + AB $$ **总结** $$ \begin{cases} \sum = A\oplus B\oplus C_{in} \\ C_{out} = (A \oplus B)C_{in} + AB \end{cases} $$

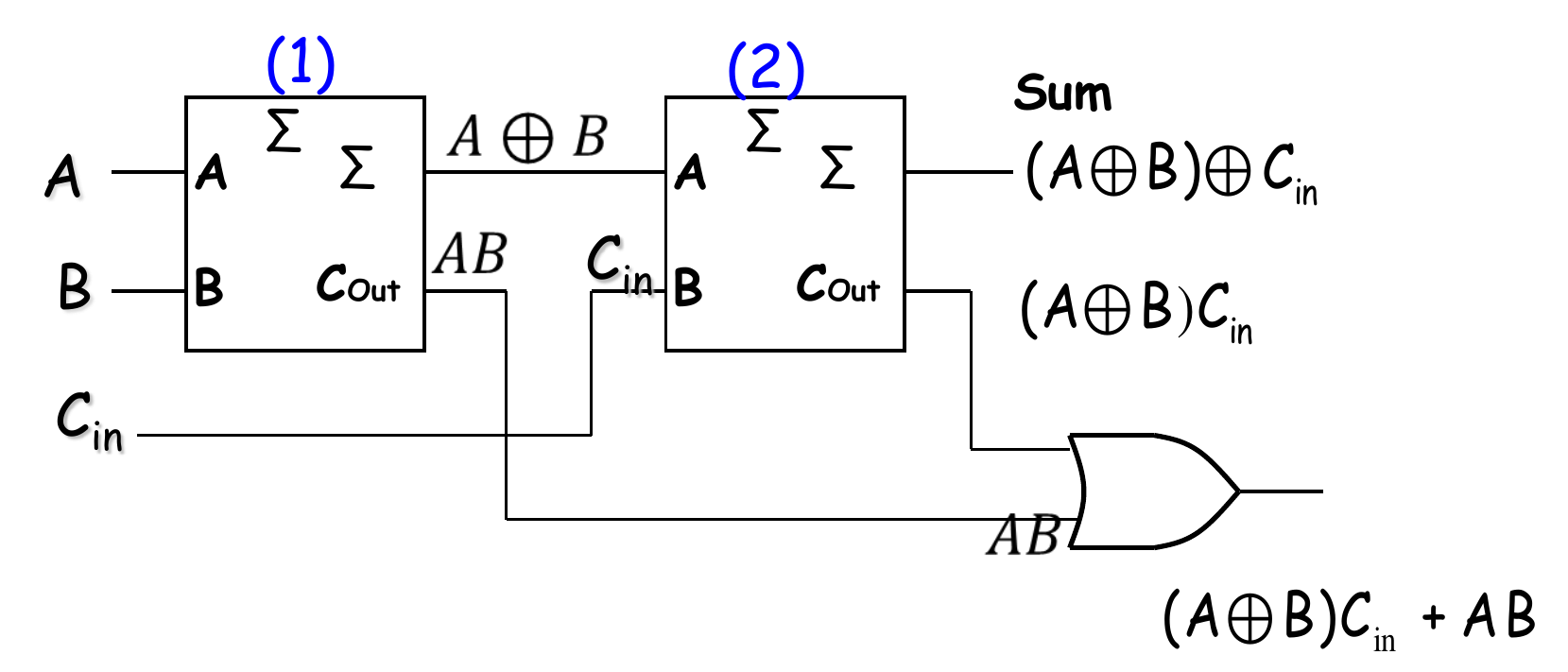
用两个半加器实现全加器

Parallel Binary Adders

Two or more full-adders are connected to form parallel binary adders.
A single full-adder is capable of adding two 1-bit binary numbers and an input carry. To add binary numbers with more than one bit, additional full-adders must be used.
The carry output of each adder is connected to the carry input of the next higher-order adder.
In terms of the method used to handle carries in a parallel adder, there are two types: the ripple carry adder and the carry look-ahead adder.

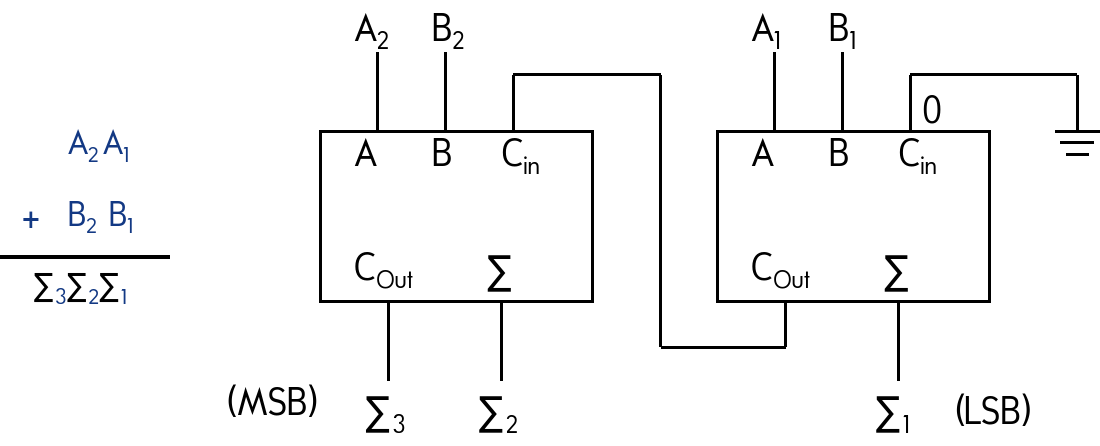
Example: 4-bit parallel adders

A group of four bits is called a nibble(半字节). A basic 4-bit parallel adder is implemented with four full-adders.

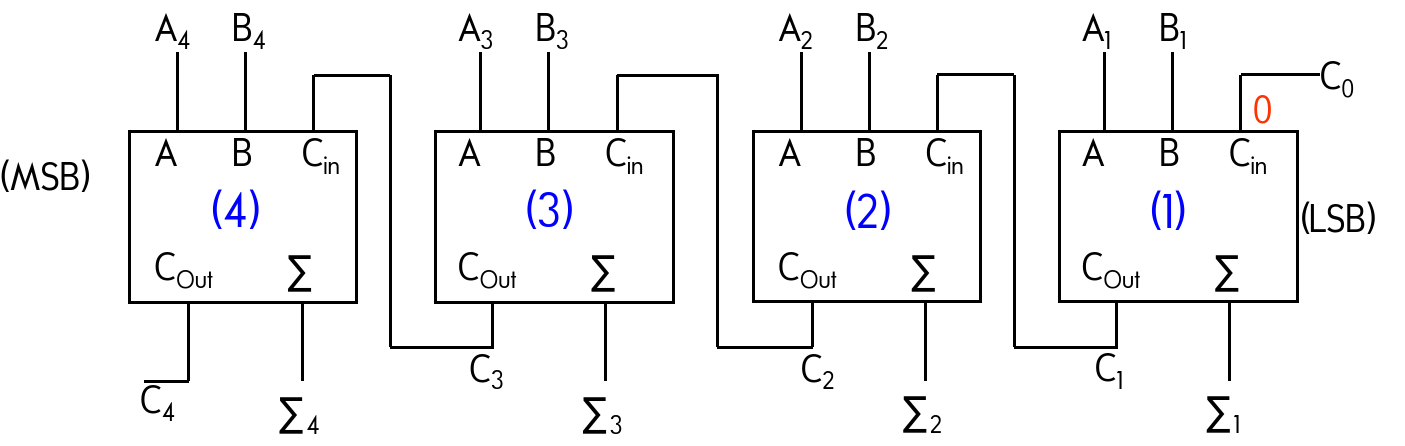
Method 1: Ripple Carry Adder (串行进位加法器) RCA

Ripple Carry Adder is one in which the carry output of each full-adder is connected to the carry input of the next higher-order stage.
The sum and the output carry of any stage cannot produced until the input carry occurs; this causes a time delay in the addition process.
完整的 $N$ 位串行进位加法器加法需要 $O(N)$ 的时间

Method 2: Look-Ahead Carry Adder (超前进位加法器) CLA

The look-ahead carry adder anticipates the output carry based on the input bits, and produces the output carry by either carry generation or carry propagation.

一个N位的CLA可以在 $O(1)$ 的时间内计算完N位的加法
CLA在位数较大的情况下，逻辑电路复杂程度会大幅增加。实际使用的时候，一般不会把一个位数很大的加法器直接以CLA的形式展开，而是以2-bit，4-bit或8-bit的CLA作为一个单元，然后把各个单元作为一个整体再用CLA的方式连起来，这样可以在计算速度和电路复杂度之间做一个权衡。这种结构的总体时间复杂度为 $O(\log N)$

基本定义和概念

进位生成 (Carry Generation) $G_i$ : 当输入 $A_i$ 和 $B_i$ 都为 1 时，无论低位的进位 $CI_i$ 是多少，本位都会产生一个向高位的进位。
$G_i = A_i B_i$
进位传播 (Carry Propagation) $P_i$ : 当输入 $A_i$ $A_{i}$ 或 $B_i$ $B_{i}$ 中有一个为 1 时 (即 $A_i+B_i=1$ $A_{i} + B_{i} = 1$ )，本位会将来自低位的进位 $CI_i$ $C I_{i}$ 传递到高位。
$P_i = A_i + B_i$ $P_{i} = A_{i} + B_{i}$
- 注意：在某些设计中，进位传播也可能定义为 $P_i = A_i \oplus B_i$ (异或)。PPT中的定义是 $P_i = A_i + B_i$ (或)。我们将按照PPT中的定义进行推导。

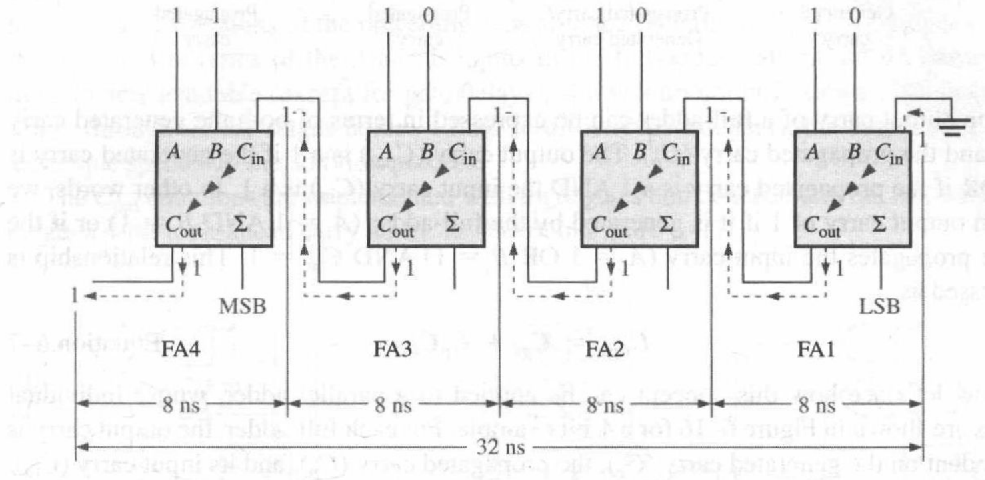
进位项推导

全加器第 $i$ 位的进位输出 $CO_i$ (Carry Out) 取决于两种情况：

本位自己产生了进位 ( $G_i = 1$ )。
本位将来自低位的进位 $CI_i$ (Carry In) 传播了上去 ( $P_i = 1$ 且 $CI_i = 1$ )。

所以，第 $i$ 位的进位输出逻辑表达式为：

$CO_i = A_i B_i + (A_i + B_i) CI_i$

使用 $G_i$ 和 $P_i$ 代替，得到：

$CO_i = G_i + P_i CI_i$

这里的 $CI_i$ 是第 $i$ 位的进位输入，它实际上就是第 $i-1$ 位的进位输出 $CO_{i-1}$ 。所以： $CI_i = CO_{i-1}$

然后进行迭代表达式循环展开，直到表达式中的所有逻辑量都是由输入直接决定的

$\begin{align} CO_i &= G_i + P_i CI_i \\ &= G_i + P_i (G_{i-1} + P_{i-1} CI_{i-1}) \\ &= G_i + P_i G_{i-1} + P_i P_{i-1} CI_{i-1} \\ &= G_i + P_i G_{i-1} + P_i P_{i-1} (G_{i-2} + P_{i-2} CI_{i-2}) \\ &= G_i + P_i G_{i-1} + P_i P_{i-1} G_{i-2} + P_i P_{i-1} P_{i-2} CI_{i-2} \\ &= \cdots \\ &= G_i + P_i G_{i-1} + P_i P_{i-1} G_{i-2} + \dots + P_i P_{i-1} \dots P_2 G_1 + P_i P_{i-1} \dots P_2 P_1 CI_1 \end{align}$

这里的 $CI_1$ 是从更低位过来的输入

注意区分题目的最低位是0还是1，这个有些题目可能是不一样的。如果最低位是0的话，那么表达式就变成

$CO_i = G_i + P_i G_{i-1} + P_i P_{i-1} G_{i-2} + \dots + P_i P_{i-1} \dots P_1 G_0 + P_i P_{i-1} \dots P_1 P_0 CI_0$

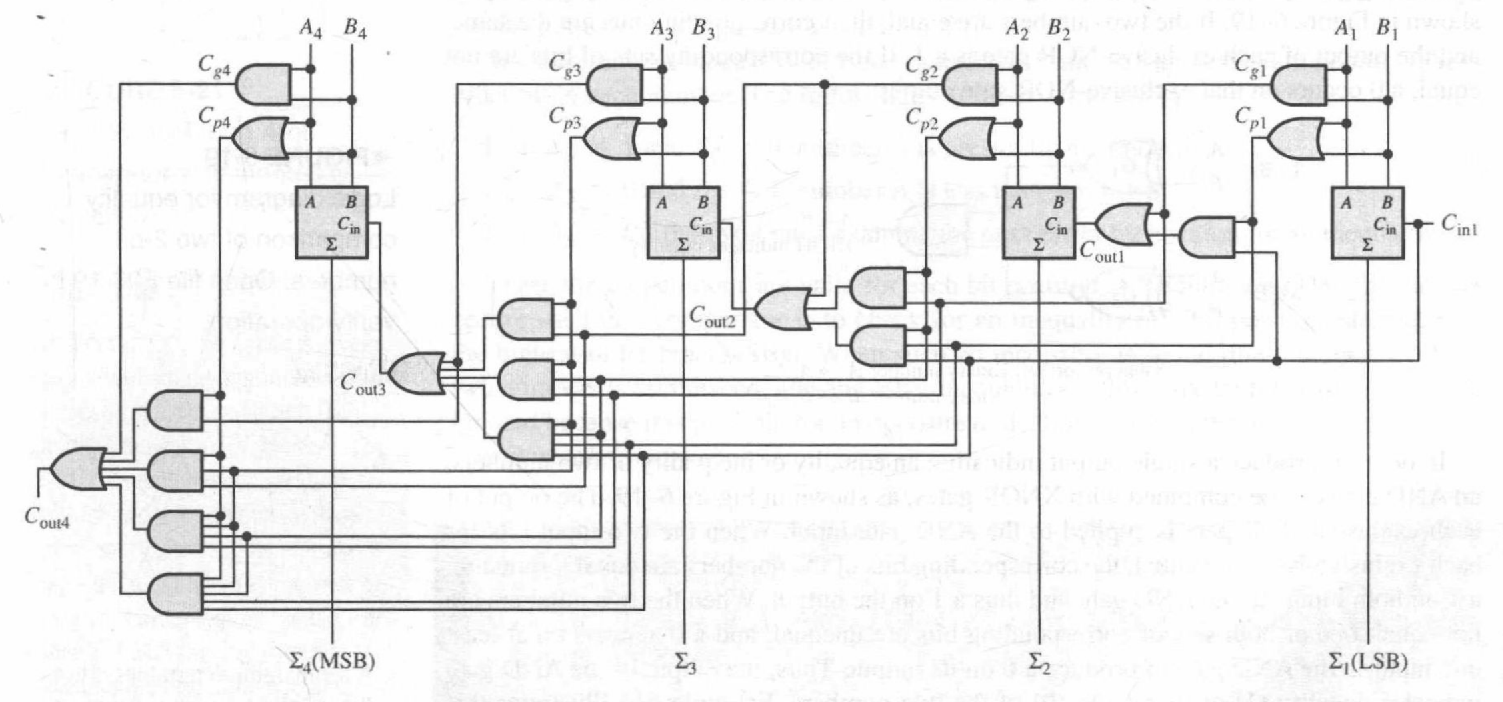
以这个4-bit CLA为例（最低位从1开始）：

$\begin{align} CO_1 &= G_1 + P_1 CI_1 \\ CO_2 &= G_2 + P_2 G_1 + P_2 P_1 CI_1 \\ CO_3 &= G_3 + P_3G_2 + P_3 P_2 G_1 + P_3 P_2 P_1 CI_1 \\ CO_4 &= G_4 + P_4G_3 + P_4P_3G_2 + P_4 P_3 P_2 G_1 + P_4 P_3 P_2 P_1 CI_1 \end{align}$

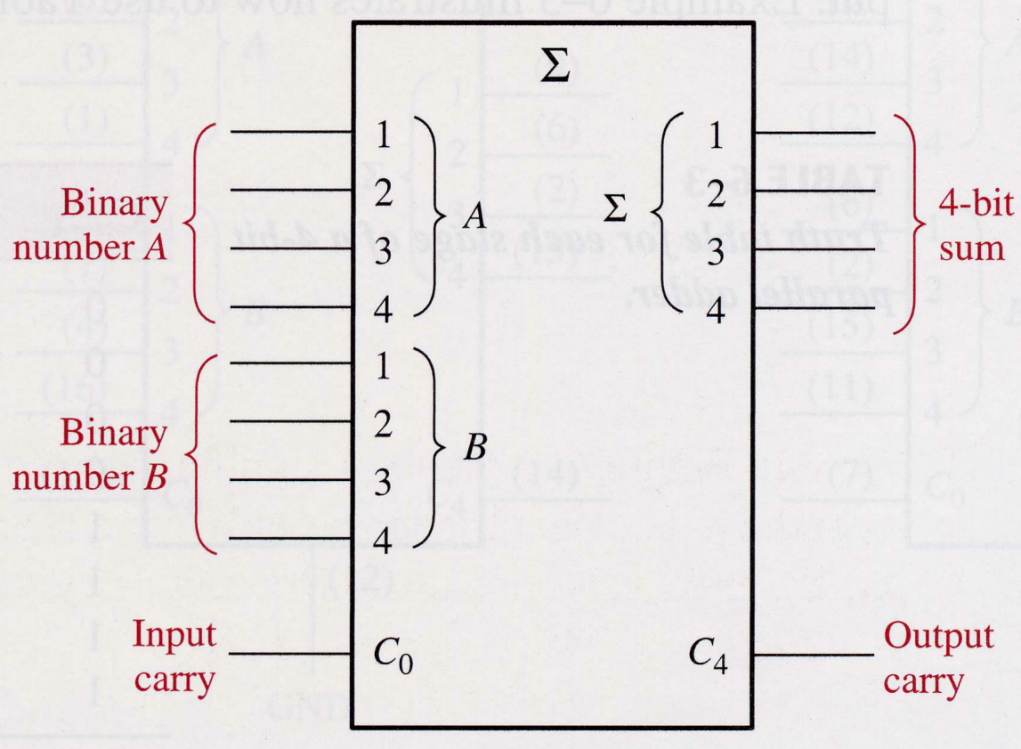
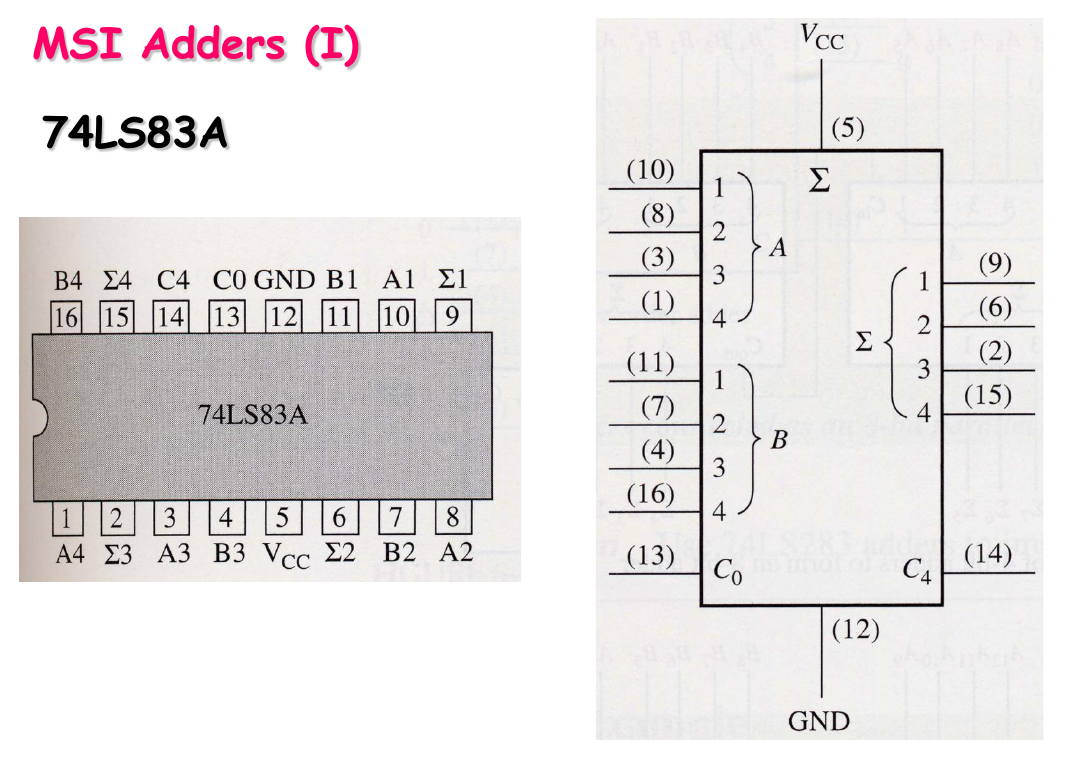
集成的加法器芯片

会用就行，知道管脚定义，会识别管脚编号，会连线扩展即可

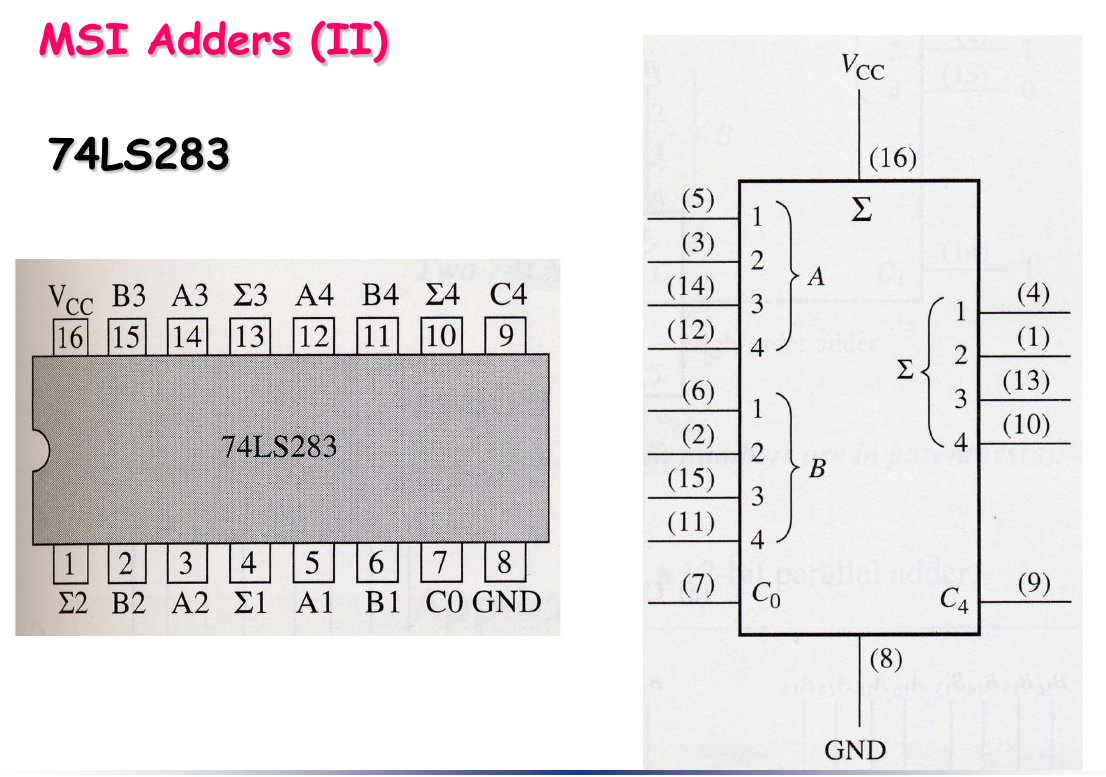
Adders Expansion

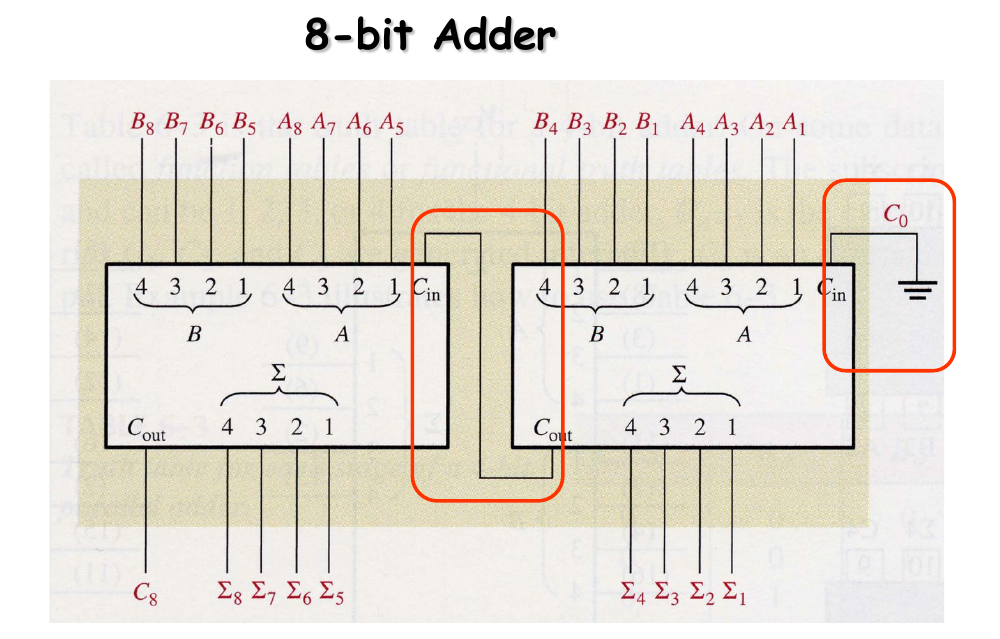
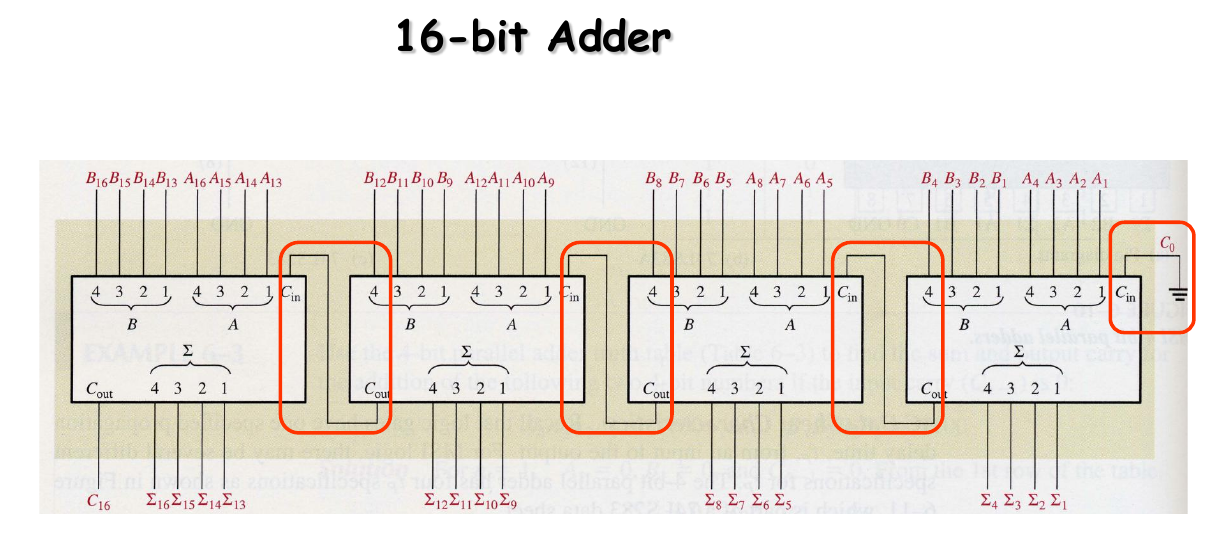
6.2 Comparators

The basic function of a comparator is to compare the magnitudes of two binary quantities to determine the relationship of those quantities.
In its simplest form, a comparator determines whether two numbers are equal.

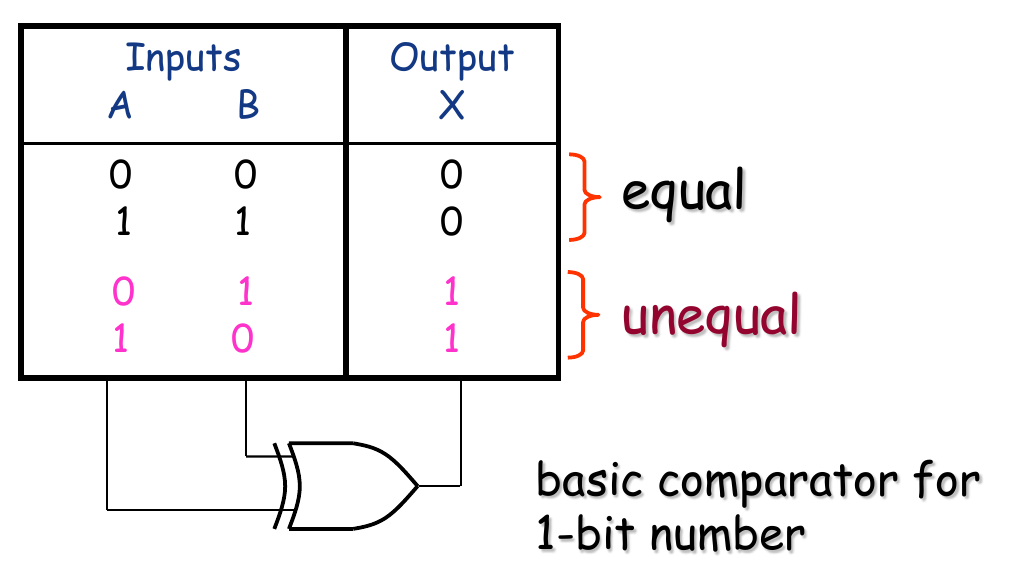
Basic Comparator

1-bit comparator

2-bit comparator

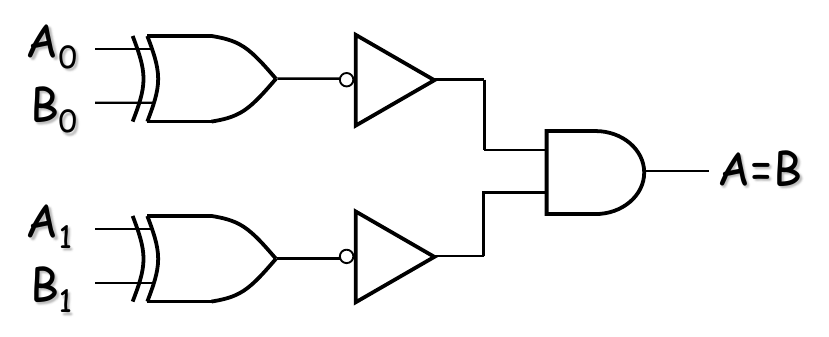
Advanced Comparators

In addition to the equality output, many comparators provide additional outputs that indicates which of the two numbers is the larger.
That is, there is an output that indicates when number A is greater than number B (A > B) and an output that indicates when number A is less than number B (A < B).

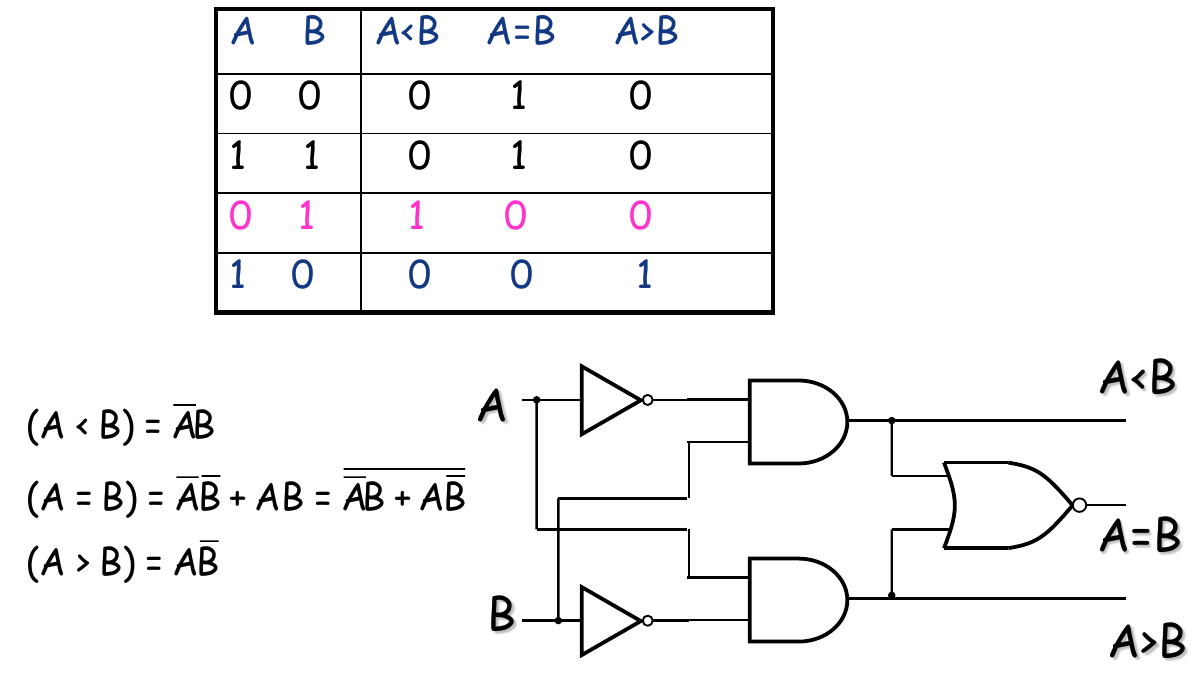
One-bit Comparator

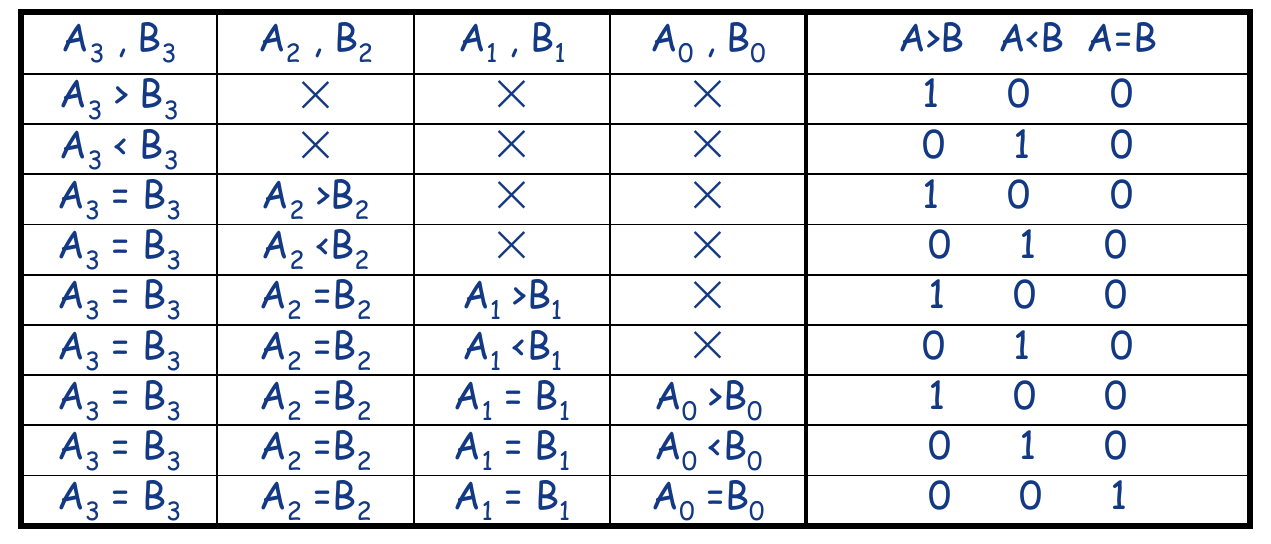
4-bit Comparator

Comparison Rules

Begin from MSB
If $A_3 > B_3$ , then $A > B$
If $A_3 < B_3$ , then $A < B$
If $A_3 = B_3$ , then compare the lower bits
Repeat this operation to LSB

Bit Comparison Logics

$A_i > B_i$ : $A_i = 1, B_i = 0; A_i \cdot \overline{B_i} = 1$
$A_i < B_i$ : $A_i = 0, B_i = 1; \overline{A_i} \cdot B_i = 1$
$A_i = B_i$ : $\overline{A_i \oplus B_i} = 1$ or $A_i \odot B_i = 1$

Truth Table

Logic Expression

$\begin{align} Y_{(A<B)} &= \bar{A}_3 B_3 + (A_3 \odot B_3)\bar{A}_2 B_2 + (A_3 \odot B_3)(A_2 \odot B_2)\bar{A}_1 B_1 \\ &+ (A_3 \odot B_3)(A_2 \odot B_2)(A_1 \odot B_1)\bar{A}_0 B_0 \\ &+ (A_3 \odot B_3)(A_2 \odot B_2)(A_1 \odot B_1)(A_0 \odot B_0)I_{(A<B)} \end{align}$

$Y_{(A=B)} = (A_3 \odot B_3)(A_2 \odot B_2)(A_1 \odot B_1)(A_0 \odot B_0)I_{(A=B)}$

$Y_{(A>B)} = Y_{(A<B)} + Y_{(A=B)}$

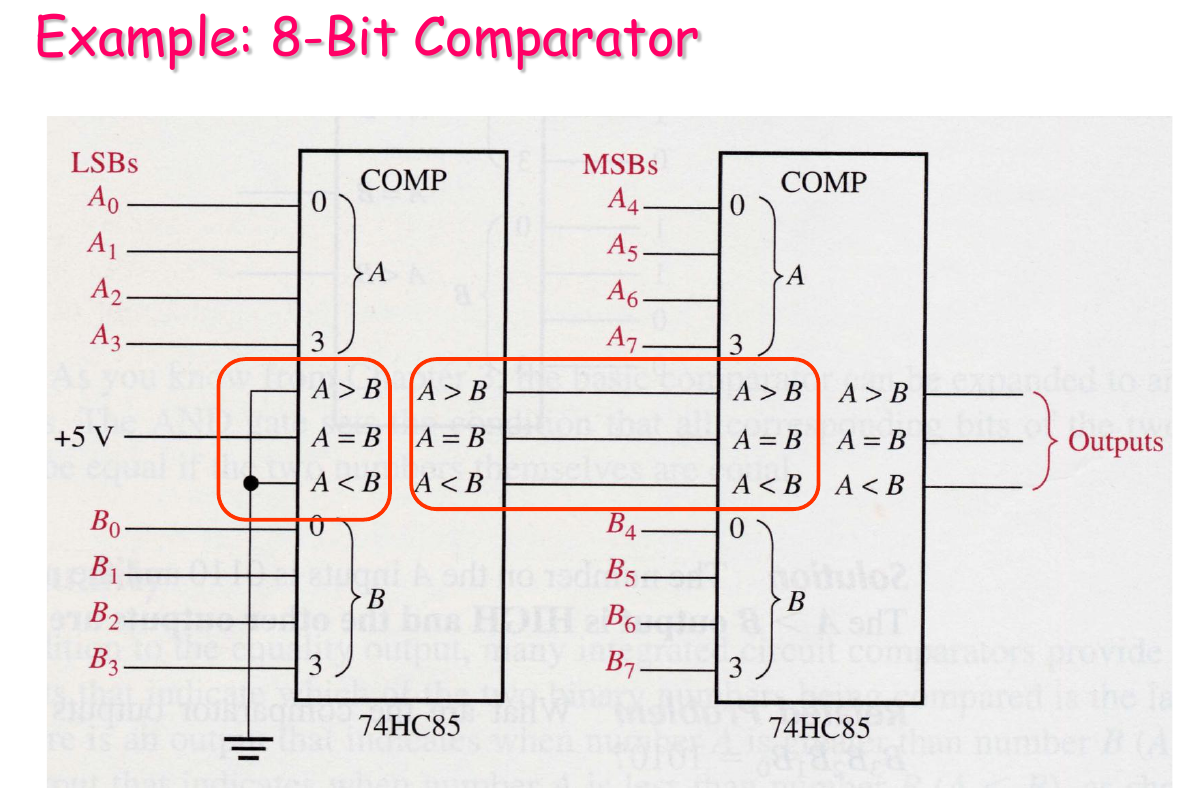
Integrated Comparator

Comparator Expansion

6.3 Decoders

The Basic function of a decoder is to detect the presence of a specified combination of bits (code) on its inputs and to indicate the presence of that code by a specified output level.
In its generation form, a decoder has n input lines to handle n bits and from one to $2^n$ output lines to indicate the presence of one or more n-bit combinations.

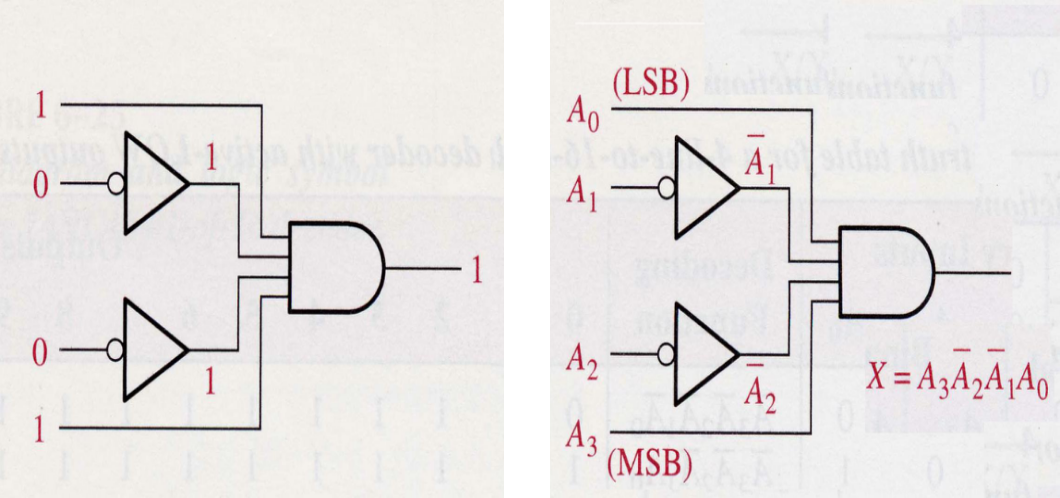
The Basic Binary Decoder

Implemented with NOT Gates & AND Gate

The 4-Bit Decoder (4-Line-to-16-Line Decoder)

In order to decode all possible combinations of four bits, sixteen decoding gates are required.
The 4-bit decoder is also called a 1-of-16 decoder because for any given code on the inputs, one of the sixteen outputs is activated.
Active-LOW (低电平有效) output is commonly used in 4-bit decoders
- An input/output pin marked with a bubble often means Active-LOW (低电平有效) input/output

Truth Table (Active-LOW Version)

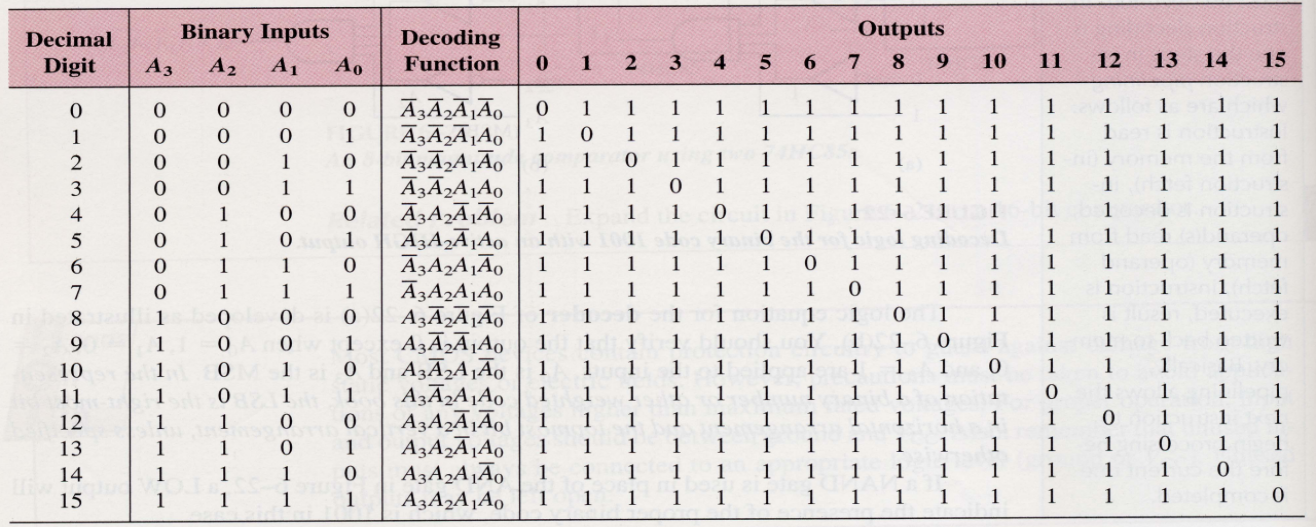
Implementation

If an active-LOW output is required for each decoded number, the entire decoder can be implemented with NAND gates and inverters.
In order to decode each of the sixteen binary codes, sixteen NAND gates are required (AND gates can be used to produce active HIGH outputs).

Logic Expression

For a 4-line-to-16-line Decoder with active-LOW output:

$Y_i = \overline{y_i} = \overline{m_i}$

Integrated 4-Bit Decoder

$Y_i = \overline{y}_i = \overline{\left(\overline{\overline{CS_1}} \times \overline{\overline{CS_2}}\right) \times m_i} = \left(\overline{CS_1} + \overline{CS_2}\right) + \overline{m}_i$

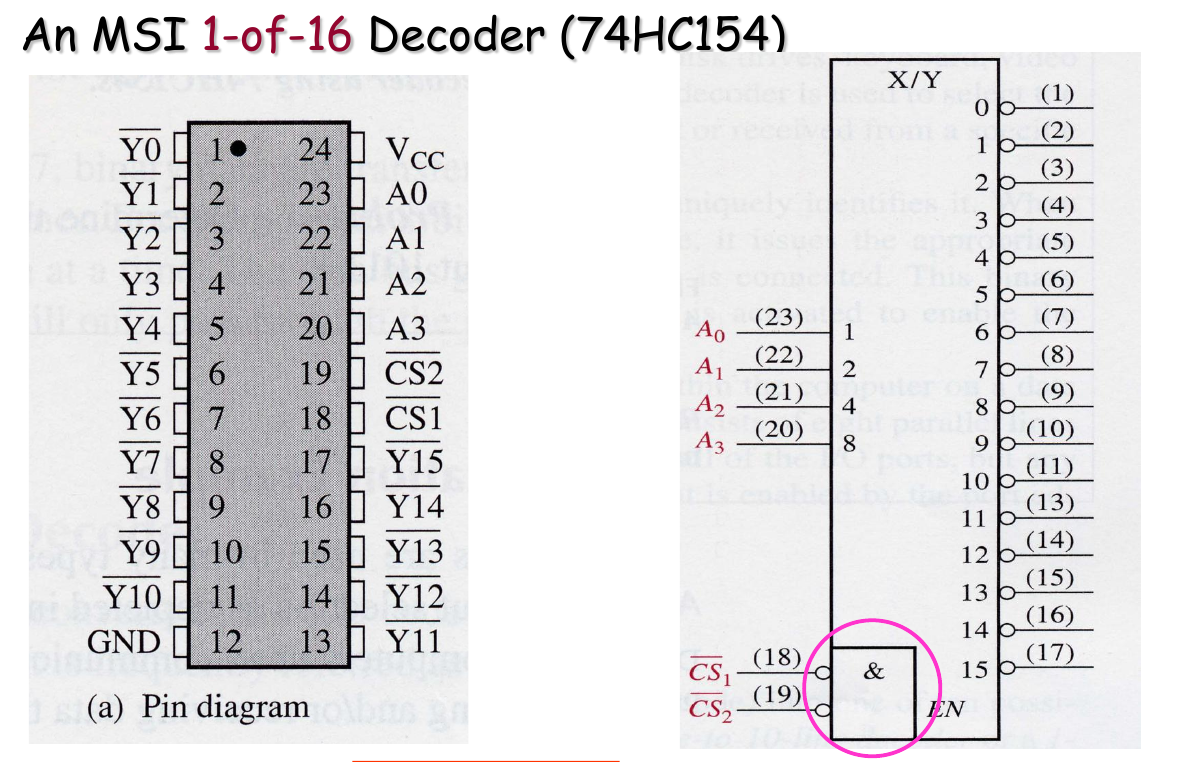
Decoder Expansion

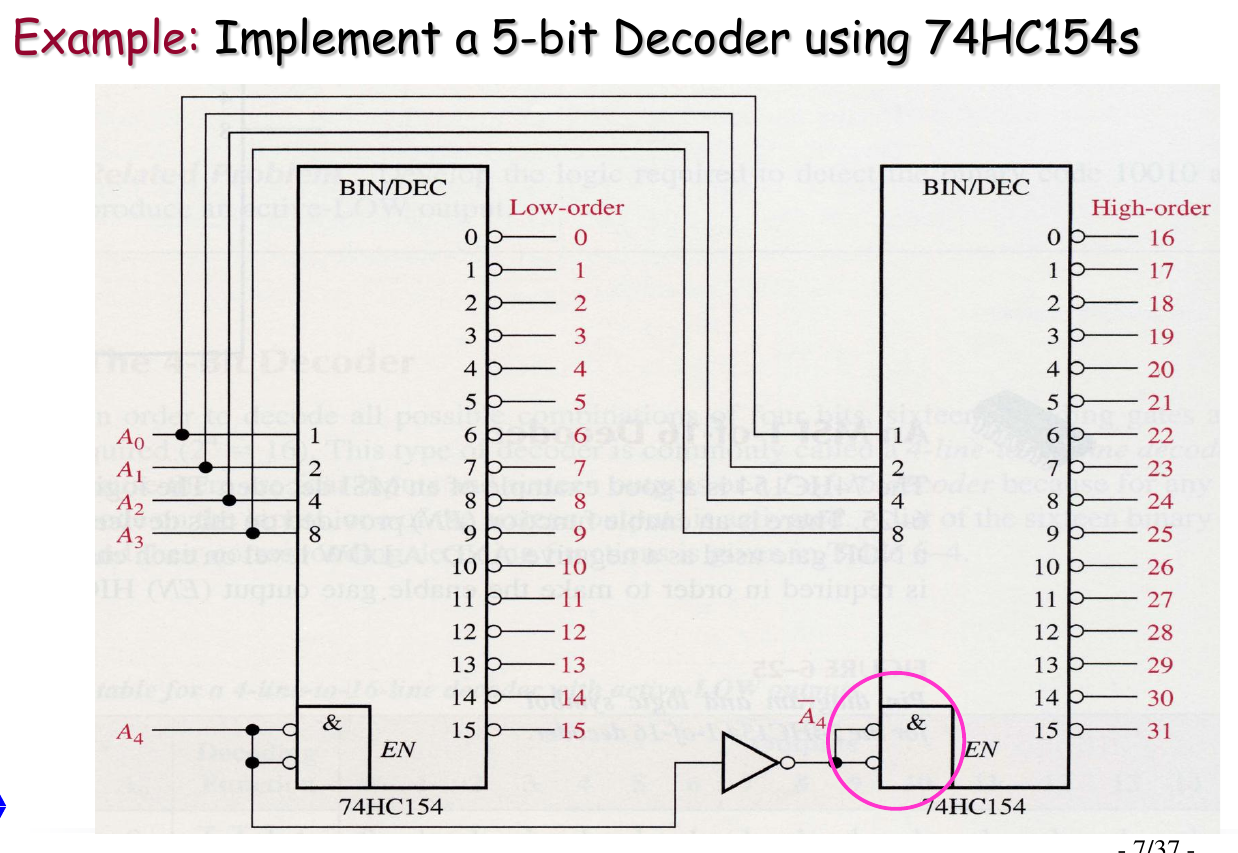
The BCD-to-Decimal Decoder

The BCD-to-Decimal Decoder converts each BCD code (8421 code) into one of ten possible decimal digit indications, usually called 4-line-to-10-line decoder or 1-of-10 decoder.

Truth Table

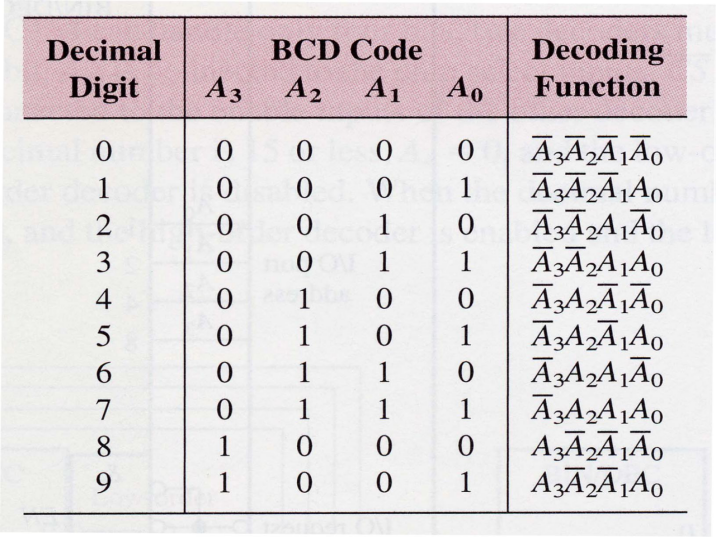
Logic Symbol & Diagram

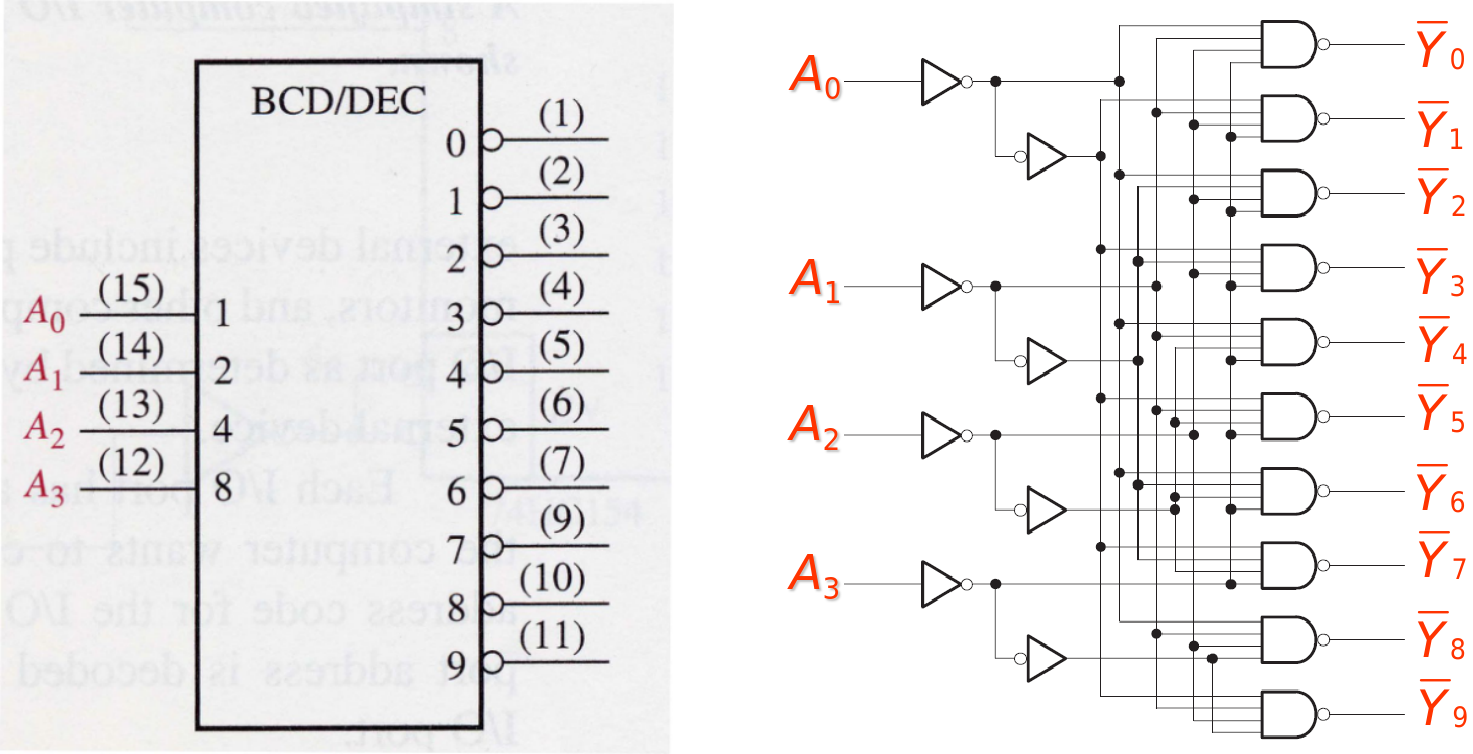
Logic Expression

$\overline{Y_i} = \overline{m_i}$

Waveform Example

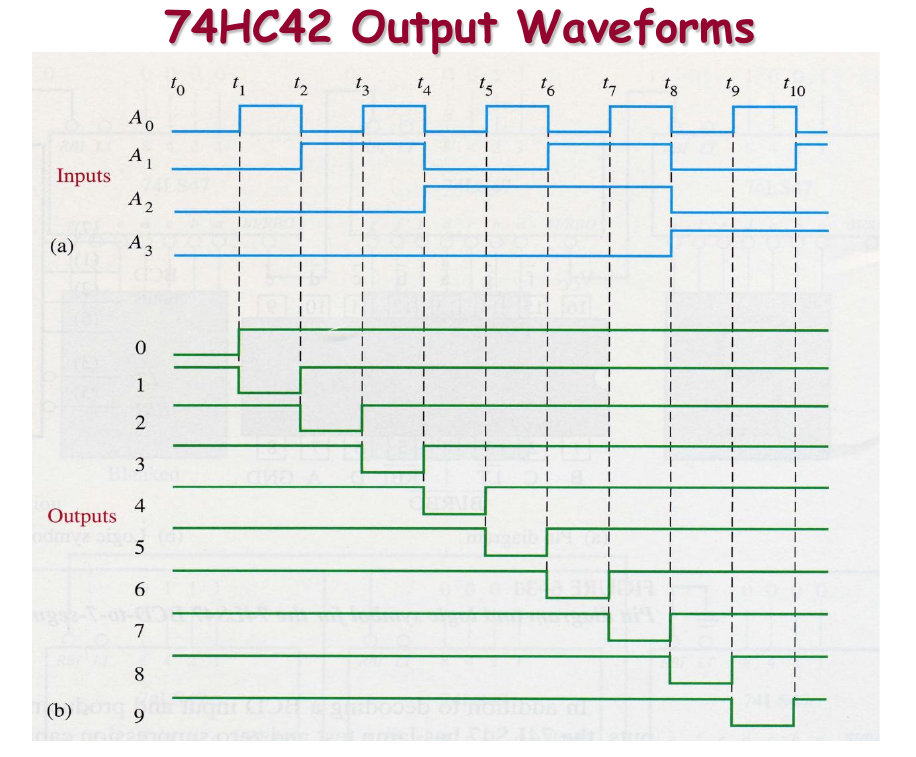
The BCD-to-7-Segement Decoder

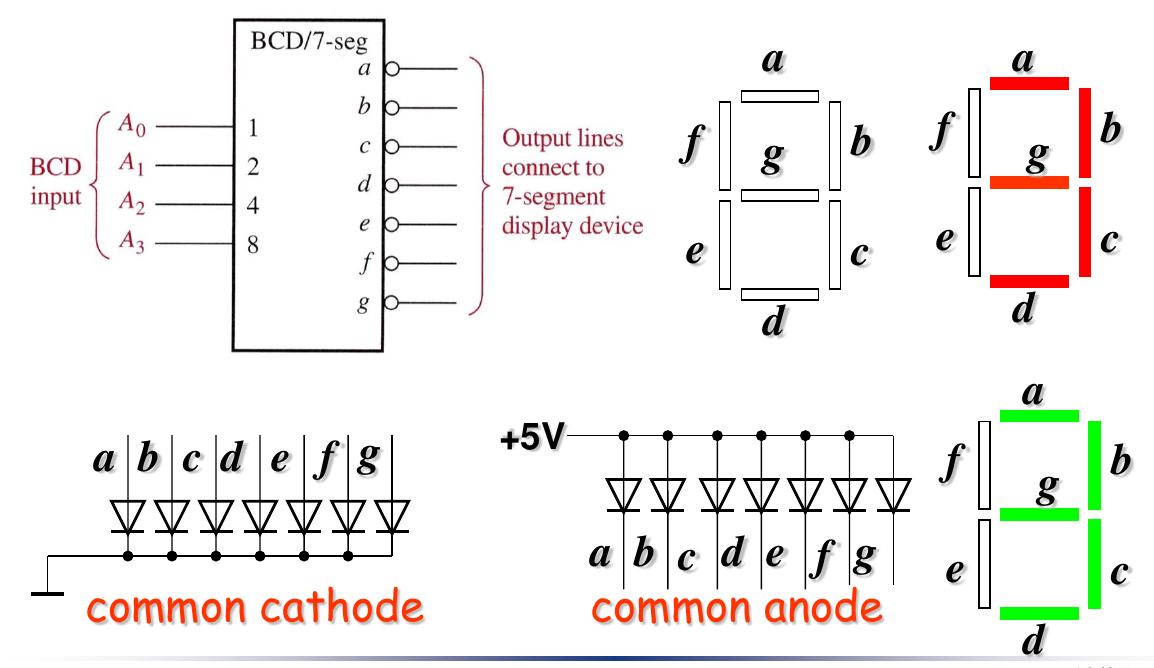
Common cathode: 共阴极
- 输入高电平的LED段亮，输入低电平的LED段暗
Common anode: 共阳极
- 输入低电平的LED段亮，输入高电平的LED段暗

Truth Table

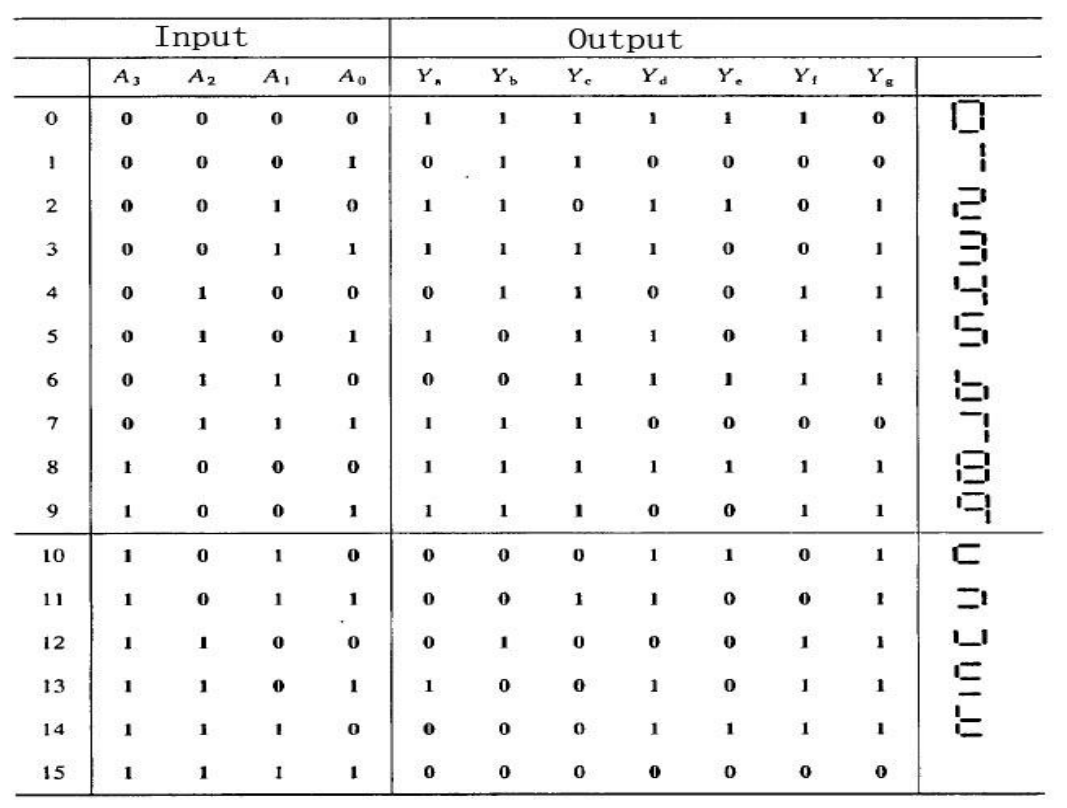
Logic Expression

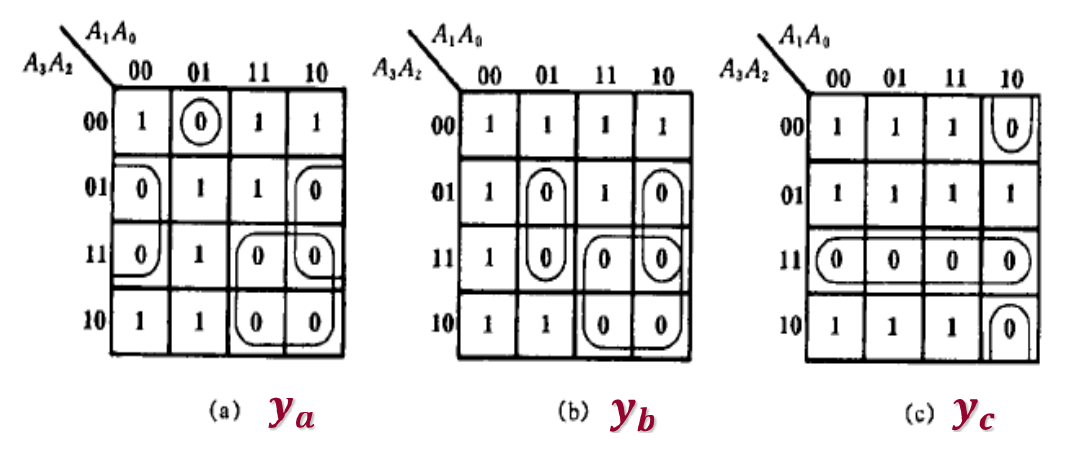
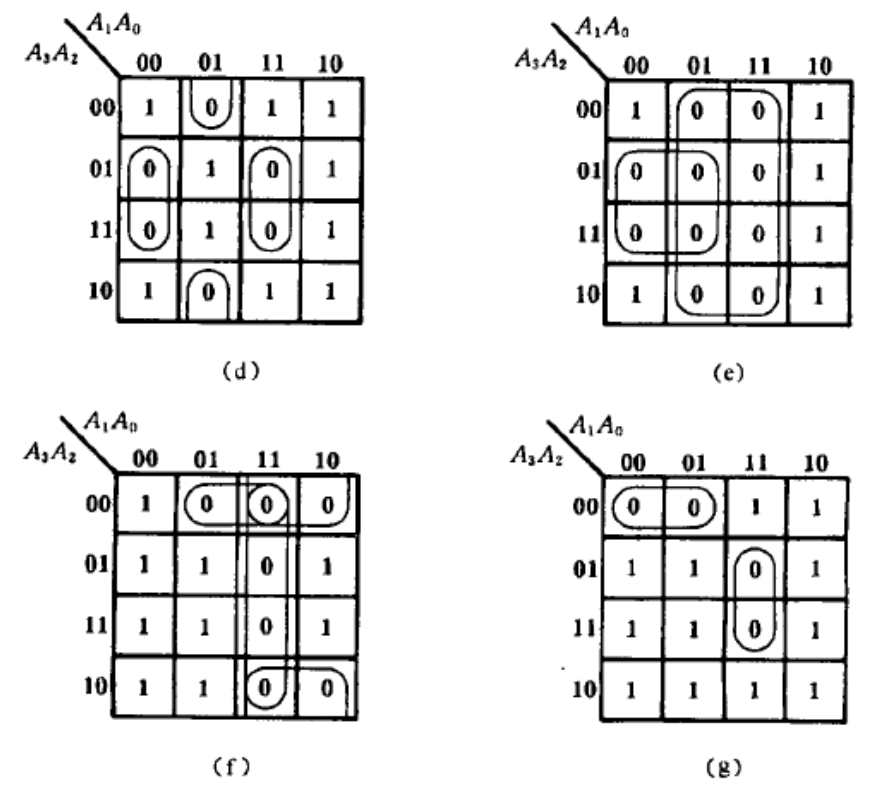
根据真值表，为每一个输出画卡诺图
- 所以写逻辑表达式之前先画真值表
- 每个输出都对应4个输入，所以是4变量卡诺图
通过卡诺图最大分组，确定每个输出的最简逻辑表达式
写出表达式，自然就知道怎么用逻辑电路实现了

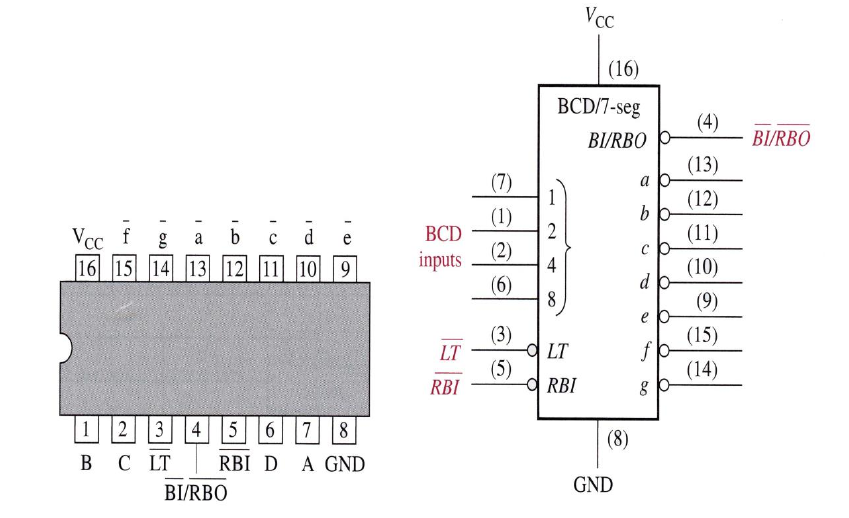
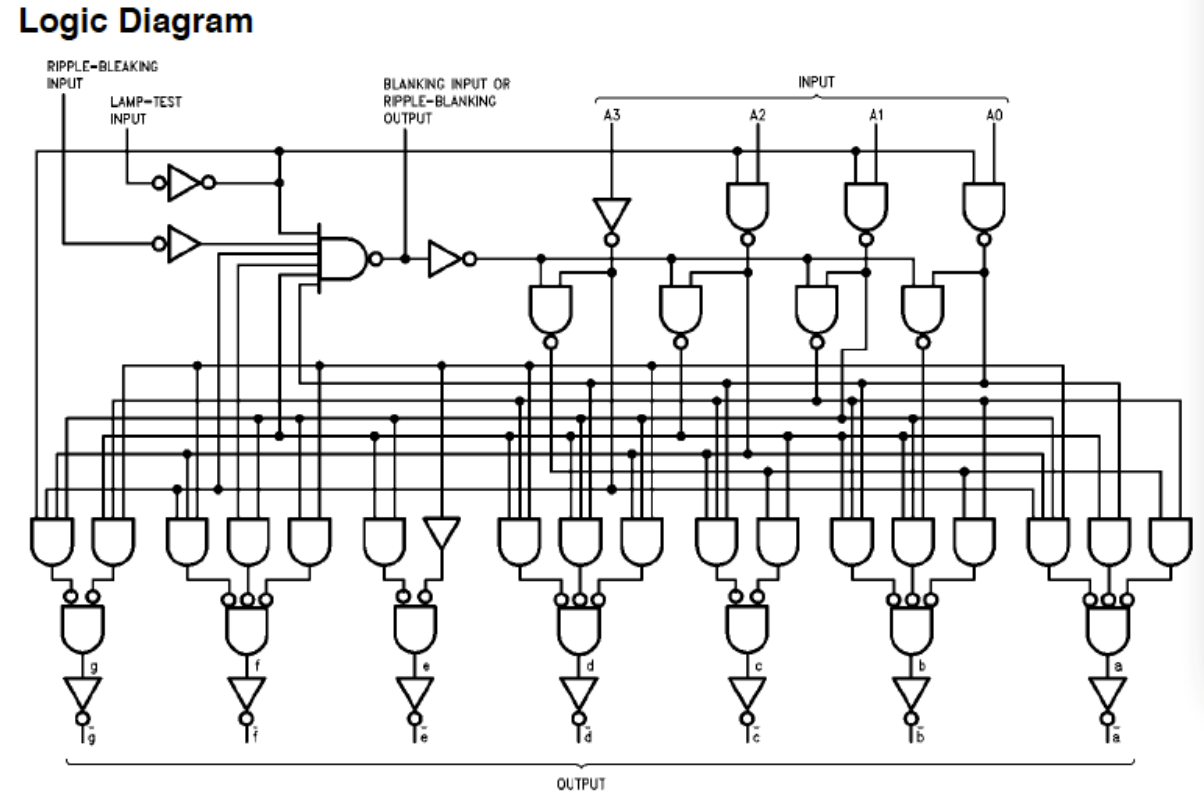
Integrated BCD-7-Segment Decoder

74LS47 is an MSI device that decode a BCD code and drives a 7-segment display.

The BCD inputs D, C, B, and A are active-HIGH.
The segment outputs a – g are active-LOW

Input pins definition

$\overline{\text{LT}}$ $\overline{LT}$ = Lamp Test . When active, all of the 7 segments are turned on. Used to verify no segments are burned out.
- 人话：灯测试，全亮
$\overline{\text{RBI}}$ $\overline{RBI}$ = Ripple Blanking Input. When active, all of the 7 segments are turned off if a zero code is on the BCD inputs and RBO will be active.
- 脉冲消隐输入/行波灭零输入
- 工作方式：在一个多位数的显示系统中（比如 4 位显示 “0025”），我们通常不希望显示前面的 “00”。RBI 用于接收来自更高位解码器的“是否需要消隐”的信号。
  - 如果 RBI 输入为高电平（通常表示更高位不是零，或者这是最高位且不需要消隐），那么当前这个解码器即使 BCD 输入为 0，也会正常显示 “0”。
  - 如果 RBI 输入为低电平（通常表示更高位是零且已经被消隐了），并且当前这个解码器的 BCD 输入也是 0 (0000)，那么这个解码器也会被消隐（不显示任何内容），并通过 RBO 输出一个低电平信号给下一位。
$\overline{BI}/\overline{RBO}$ $\overline{B I} / \overline{RBO}$ = Blanking Input/ Ripple Blanking Output. When active, all of the 7 segments are turned off.
- 消隐输入 / 脉冲消隐输出
- 作为 BI (Blanking Input - 消隐输入): 当这个管脚被强制设置为低电平（通常情况下）时，它会无条件地关闭所有七段输出（a-g），使得显示器熄灭（Blanking），无论 BCD 输入或 LT 输入状态如何（但有时 LT 会覆盖 BI）。这可以用于完全关闭某个数位的显示。
- 作为 RBO (Ripple Blanking Output - 脉冲消隐输出 / 行波灭零输出): 这个输出状态取决于 RBI 输入和当前的 BCD 输入值。
  - 条件: 只有当 RBI 输入为低电平 并且当前解码器的 BCD 输入为 0 (0000) 时，RBO 输出才会变为低电平。
  - 其他情况: 在所有其他情况下（即 RBI 为高电平，或者 BCD 输入不是 0），RBO 输出将保持高电平。

Leading Zero Suppression (前导零抑制)

目标: 消除数字整数部分开头多余的零。例如，将 “0075” 显示为 " 75"。
方向: 消隐信号从最高位 (MSD) 向最低位 (LSD) 传递。
接法:
1. 最高位 (MSD) 解码器:
  - 将其 RBI (Ripple Blanking Input - 行波消隐输入) 引脚接低电平 (GND)。这使得最高位如果其BCD输入为0，它自身就会被消隐。
2. 中间各位解码器:
  - 将前一位（更高位）解码器的 RBO (Ripple Blanking Output) 引脚连接到当前位解码器的 RBI 引脚。
  - 这个链式连接从MSD的下一位一直持续到LSD的前一位。
3. 最低位 (LSD) 解码器:
  - 如果希望数字 “0000” 显示为一个 “0”: 将LSD解码器的 RBI 引脚接高电平 (VCC) 或不接。这样即使更高位都因是0而被消隐，LSD也不会被消隐，从而显示出0。
  - 如果希望数字 “0000” 完全显示为空白: 则LSD的RBI也按上述链式连接接入（即连接到其前一位的RBO）。
  - 最低位（LSD）通常RBO通常不接

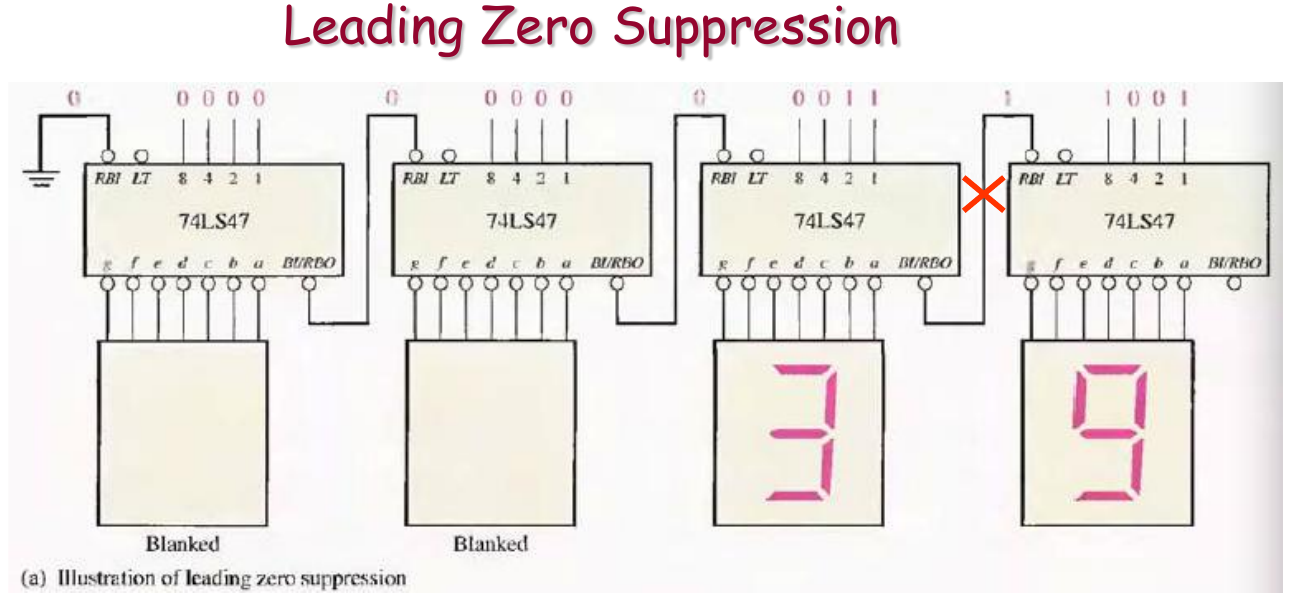
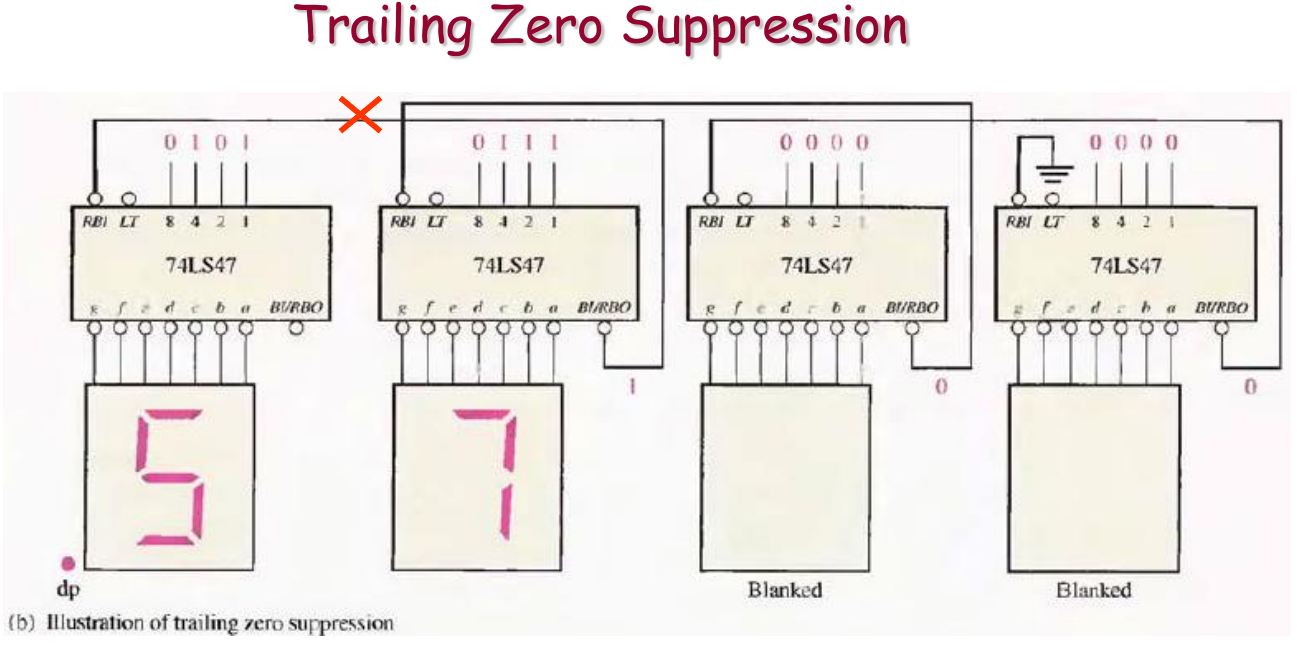
Trailing Zero Suppression (后续零抑制 / 末尾零抑制)

目标: 通常用于消除数字小数部分末尾多余的零。例如，将 “12.500” 显示为 “12.5”。
方向: 消隐信号从小数部分的最低位 (LSD of fractional part) 向小数部分的最高位 (MSD of fractional part, 即小数点后的第一位) 传递。
接法 (仅针对小数部分):
1. 小数部分的最低位解码器:
  - 将其 RBI 引脚接低电平 (GND)。这使得小数部分的最低位如果其BCD输入为0，它自身就会被消隐。
2. 小数部分的中间各位解码器 (从低位向高位):
  - 将后一位（更低位）解码器的 RBO 引脚连接到当前位解码器的 RBI 引脚。
  - 这个链式连接从小数部分LSD的上一位一直持续到小数点后的第一位。
3. 小数点后第一位解码器 (小数部分的最高位):
  - 如果希望小数部分0000显示成一个0，那小数部分的最高位可以接高电平（VCC）或不接
  - 如果希望小数部分0000完全显示成空白，那么其RBI也按上述链式连接接入（即连接到后一位的RBO），就其RBI会接收来自小数部分下一位（更低位）的RBO信号。
整数部分: 整数部分的解码器通常不参与后续零抑制的RBI/RBO链，它们可能采用前导零抑制的接法，或者不进行任何消隐。

实际用的时候不太用这些原始方法做零抑制的，用MCU编写程序处理零抑制和小数点位置，更灵活和方便。

6.4 Encoders

An encoder is a combinational logic circuit that essentially performs a “reverse” decoder function.
An encoder accepts an active level on one of its inputs representing a digit, such as a decimal or octal digit, and converts it to a coded output, such as BCD or binary. Encoders can also be devised to encode various symbols and alphabetic characters. The process of converting from familiar symbols or number to a coded format is called encoding.

The Decimal-to-BCD Encoder

The decimal-to-BCD encoder has ten inputs – one for each decimal digit and four outputs corresponding to the BCD code.

Simple Encoder

This kind of encoder works only when one input is active (HIGH) at a time, otherwise it will result in incorrect outputs.

Priority Encoder

The priority function means that the encoder will produce a BCD output corresponding to the highest-order digit input that is active and ignore any other lower-order active inputs.

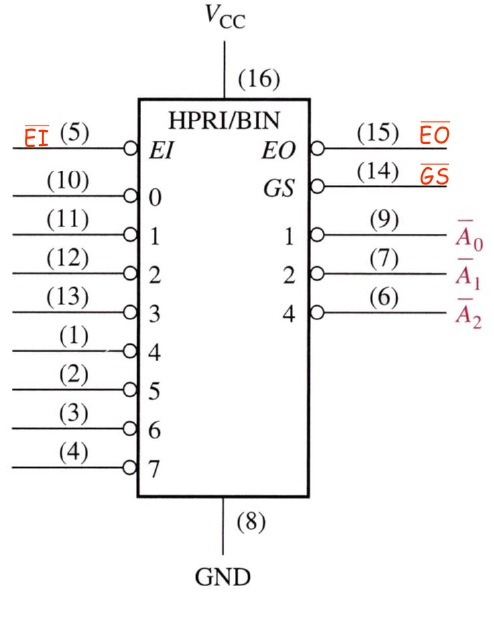
8-Line-to-3-line priority encoder

74F148 is a 8-Line-to-3-line priority encoder that has eight active-LOW inputs and three active-LOW binary outputs. The device can be used for converting octal inputs to a 3-bit binary code.

All inputs and outputs are active LOW.
$\overline{\text{EI}}$ = Enable Input. When inactive, all outputs are deactivated.
$\overline{\text{EO}}$ = Enable output. EO is active if EI is active and none of the inputs is active.
$\overline{\text{GS}}$ = Gate Strobe. GS is active if EI is active and any of the inputs is active.

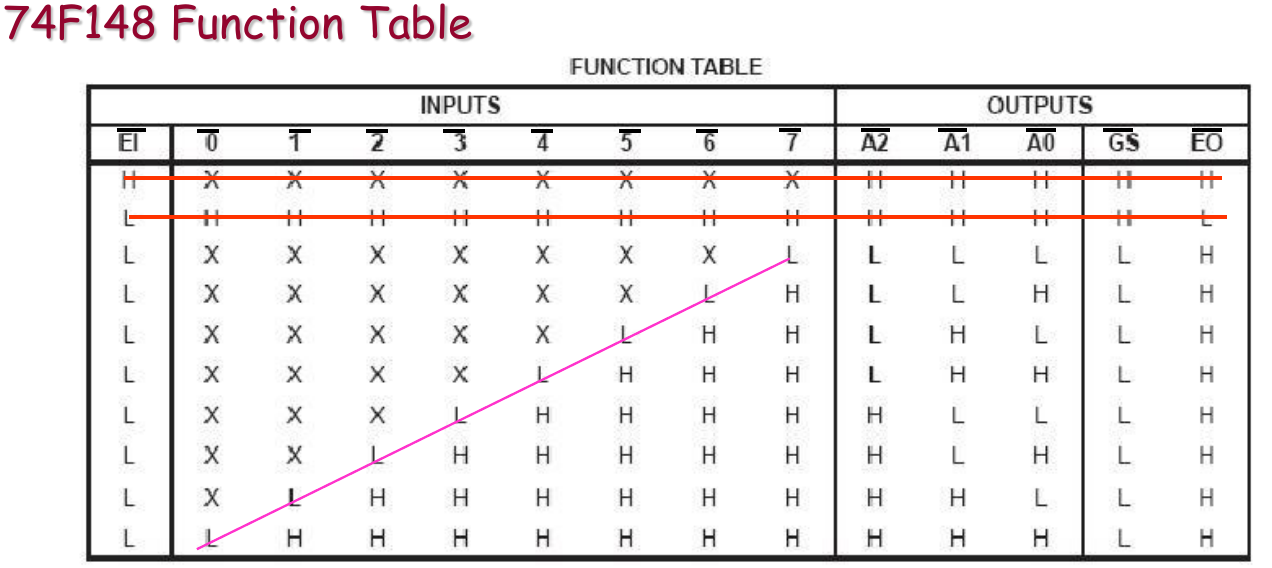
Truth Table

Logic Expression

$\begin{cases} \overline{A_2} = \overline{(I_4 + I_5 + I_6 + I_7) \cdot EI} \\ \overline{A_1} = \overline{(I_2 \overline{I_4} \cdot \overline{I_5} + I_3 \overline{I_4} \cdot \overline{I_5} + I_6 + I_7) \cdot EI} \\ \overline{A_0} = \overline{(I_1 \overline{I_2} \cdot \overline{I_4} \cdot \overline{I_6} + I_3 \overline{I_4} \cdot \overline{I_6} + I_5 \overline{I_6} + I_7) \cdot EI} \\ \overline{EO} = \overline{\overline{I_0} \cdot \overline{I_1} \cdot \overline{I_2} \cdot \overline{I_3} \cdot \overline{I_4} \cdot \overline{I_5} \cdot \overline{I_6} \cdot \overline{I_7} \cdot (EI)} \\ \overline{GS} = \overline{(I_0 + I_1 + I_2 + I_3 + I_4 + I_5 + I_6 + I_7) \cdot EI} \end{cases}$

Logic Diagram

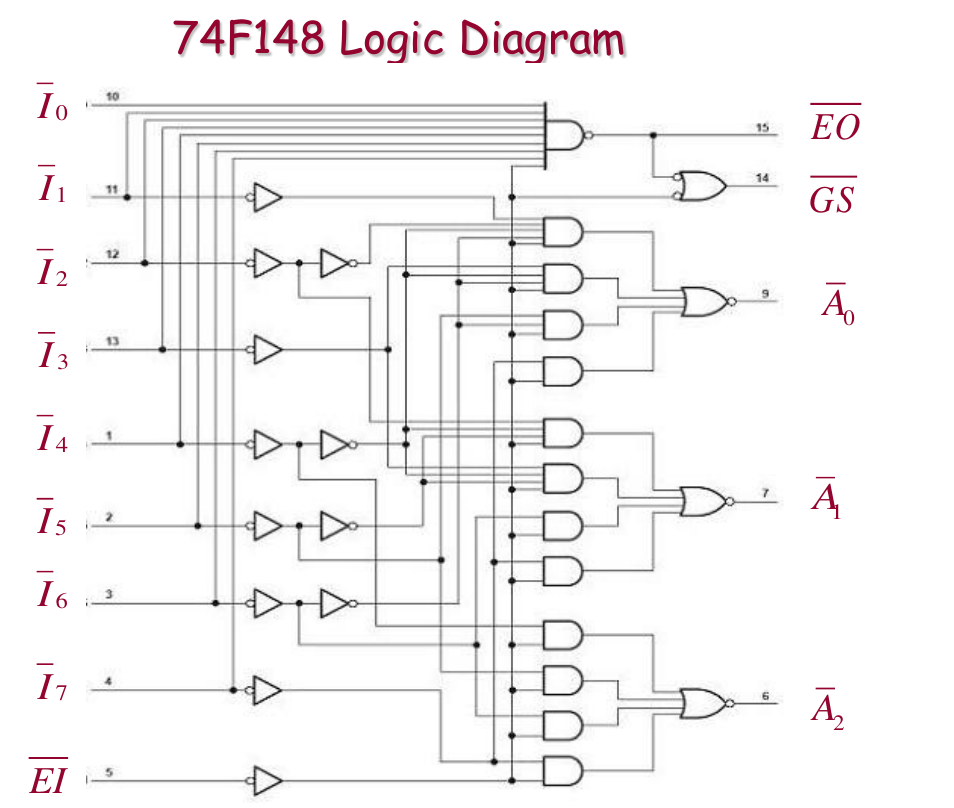
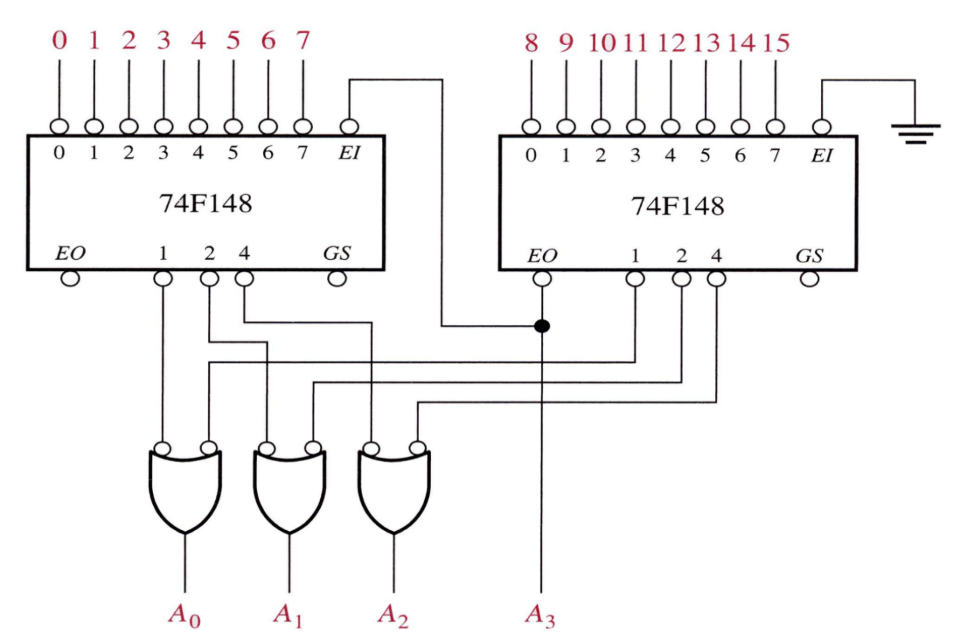
Expansion: 16-4 Priority Encoder

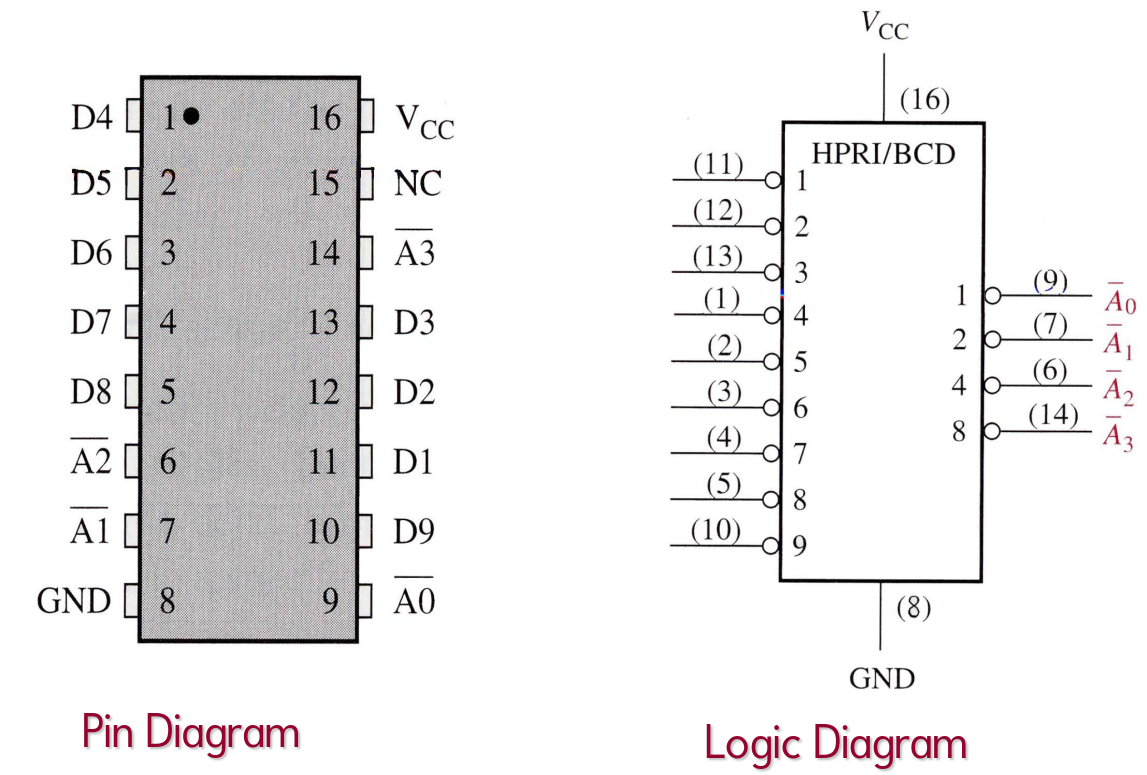
The Decimal-to-BCD Priority Encoder

The Decimal-to-BCD priority encoder means that the encoder will produce a BCD output corresponding to the highest-order decimal digit input that is active and ignore any other lower-order active inputs.

74HC147 is a priority encoder with active-LOW inputs (0) for decimal digits 1 through 9, and active-LOW BCD outputs. A BCD zero output is represented when none of the inputs is active.

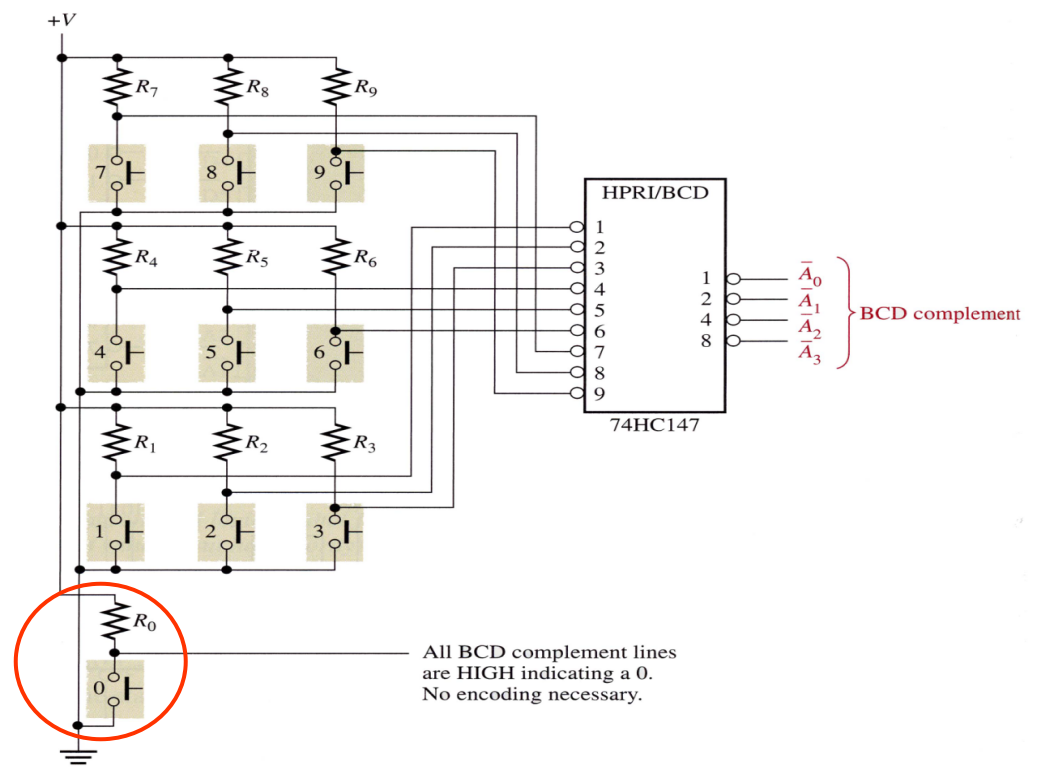
Application example: Simplified keyboard encoder

6.5 Code Converters

A code converter converts one code to another.

BCD-Binary Conversion

Determine the value or weight of each bit in the BCD number, and represent it by a binary number;
Add all the weights that the corresponding bits are 1s;
The result of this addition is the binary equivalent of the BCD number.

Example

Convert the BCD numbers 0010 0111 to binary

The weights of each bit as follows:

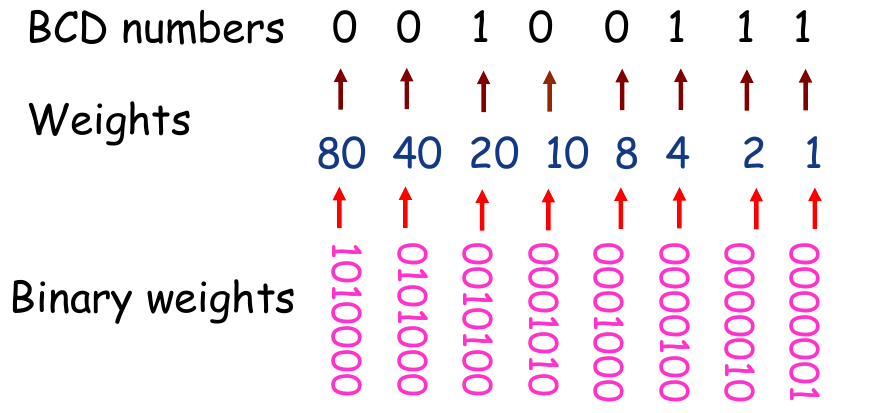
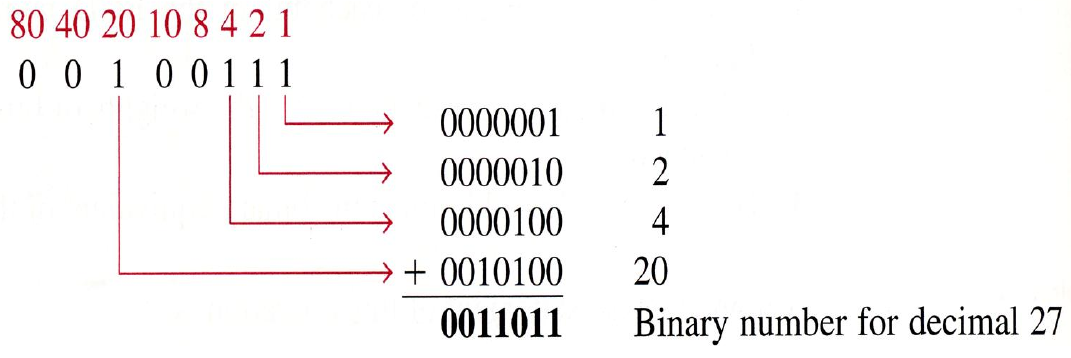
Sum of the weights:

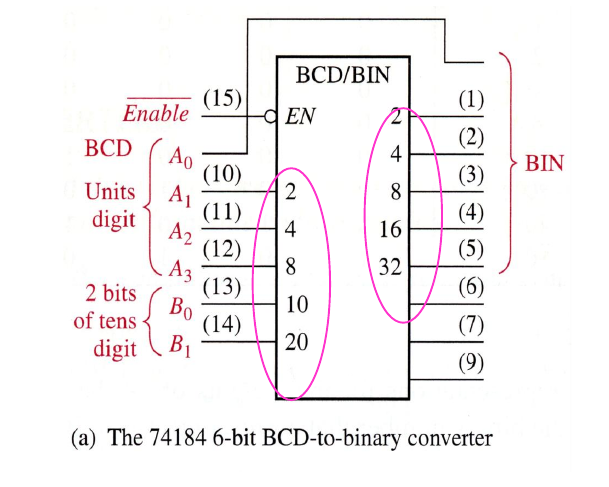
Integrated Conversion Chip

一个有趣的现象： $A_0$ 不需要处理，因为BCD码的LSB和对应二进制的LSB必然是一致的（想一想就能明白）

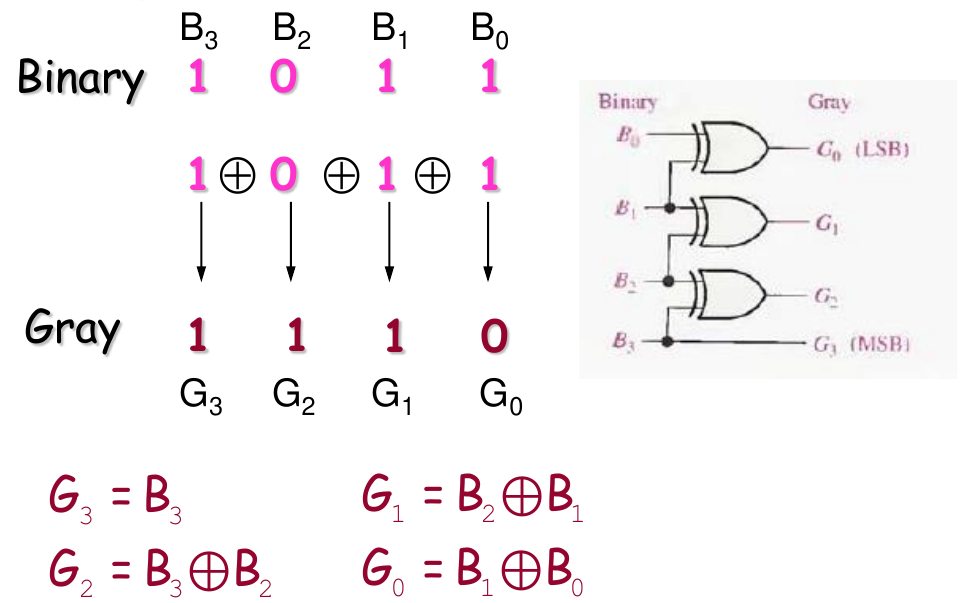
Binary-to-Gray Conversion

XOR gates can be used for the conversions
记住：如果要画二进制/格雷码互转的逻辑电路图，从MSB开始画

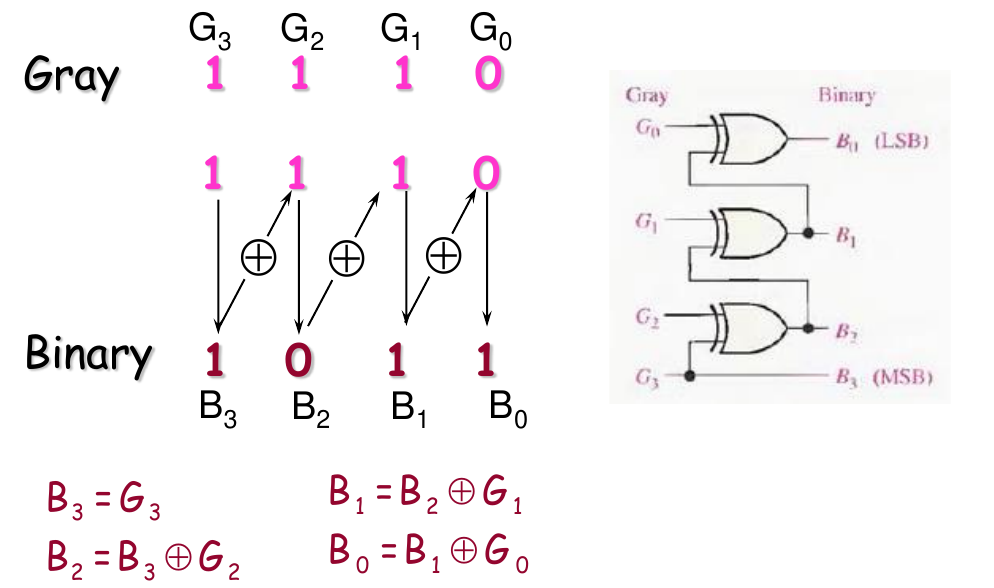
Gray-to-Binary Conversion

XOR gates can be used for the conversions
记住：如果要画二进制/格雷码互转的逻辑电路图，从MSB开始画
注意：处理一位Gray Code的XOR Gate的输入连的是这一位的Gray Code和高一位的Binary Code转换结果，MSB直接输出，与Binary转Gray是不同的，别搞混了

6.6 Multiplexers

A multiplexer (MUX) is a device that allows digital information from several sources to be routed onto a single line for transmission over that line to a common destination.

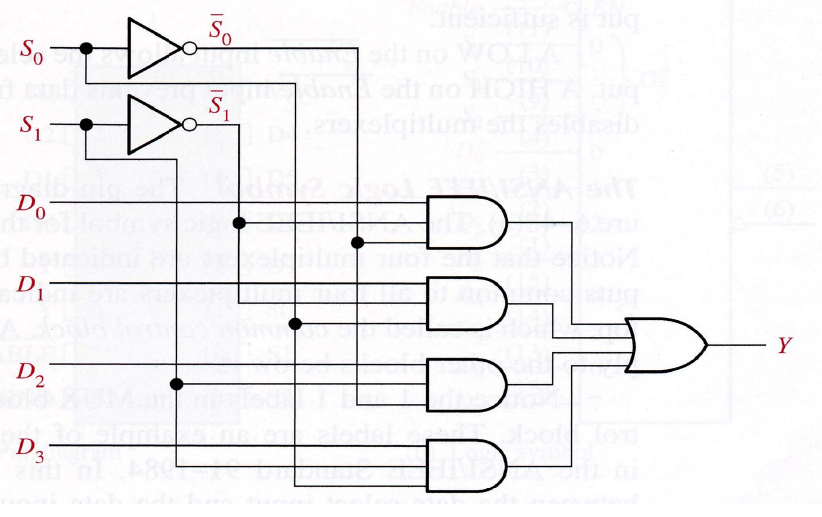
4-bit data selector

Logic Expression

$Y = \overline{S_1} \cdot\overline{S_0}D_0 + \overline{S_1}S_0D_1 + S_1\overline{S_0}D_2 + S_1S_0D_3 = m_0D_0 + m_1D_1 + m_2D_2 + m_3D_3$

Logic Diagram

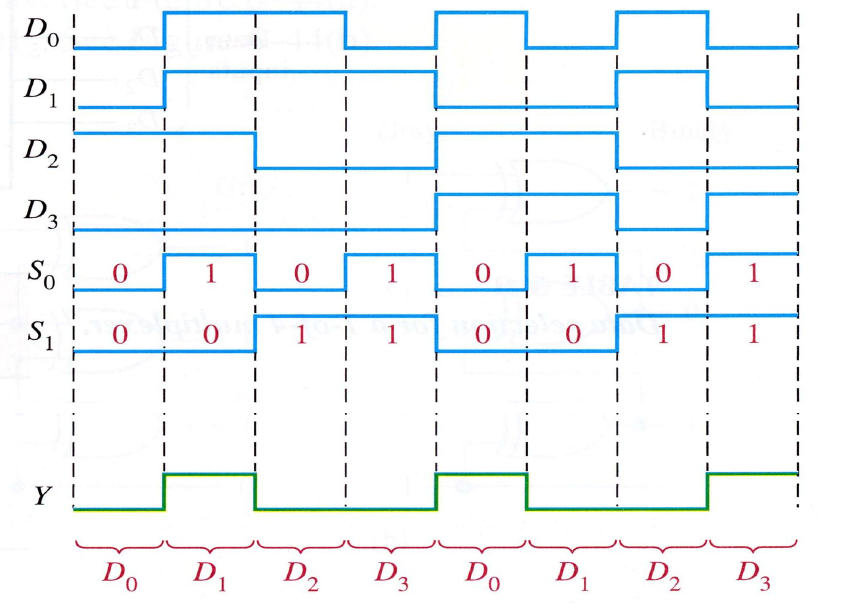
Integrated Multiplexer

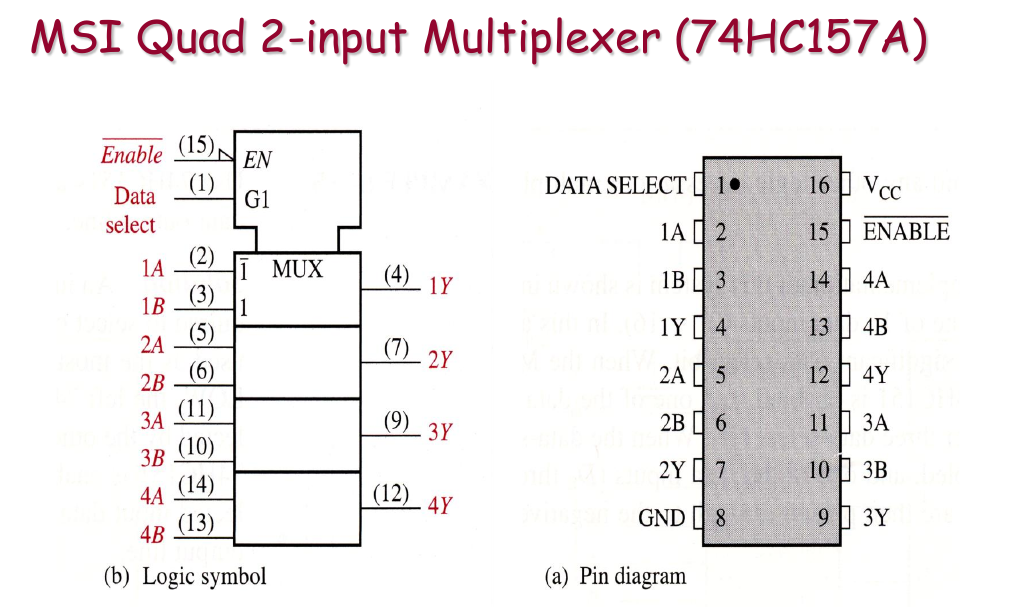
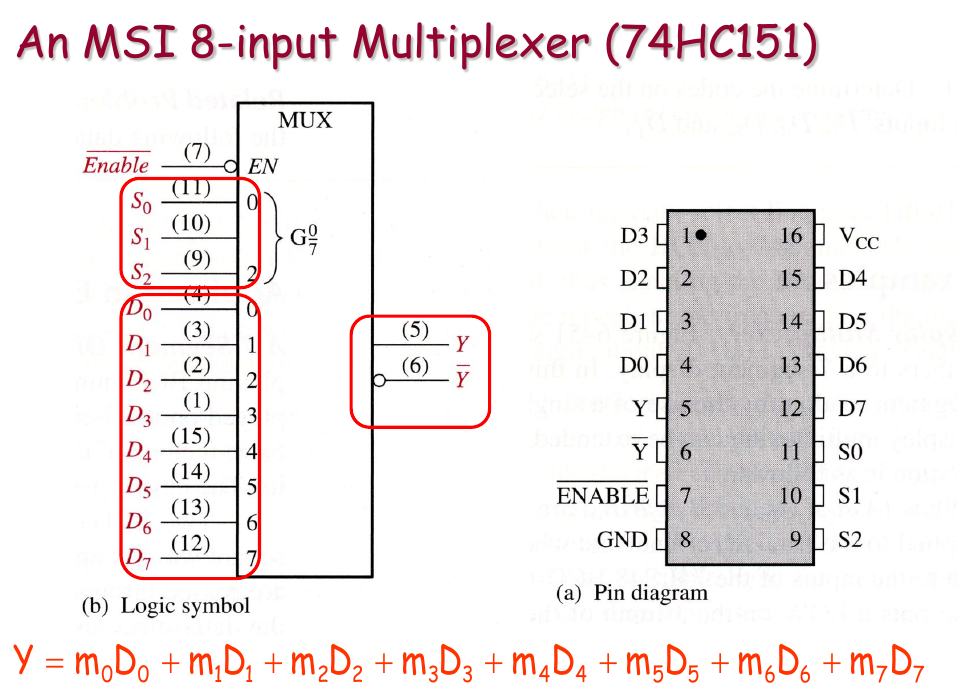
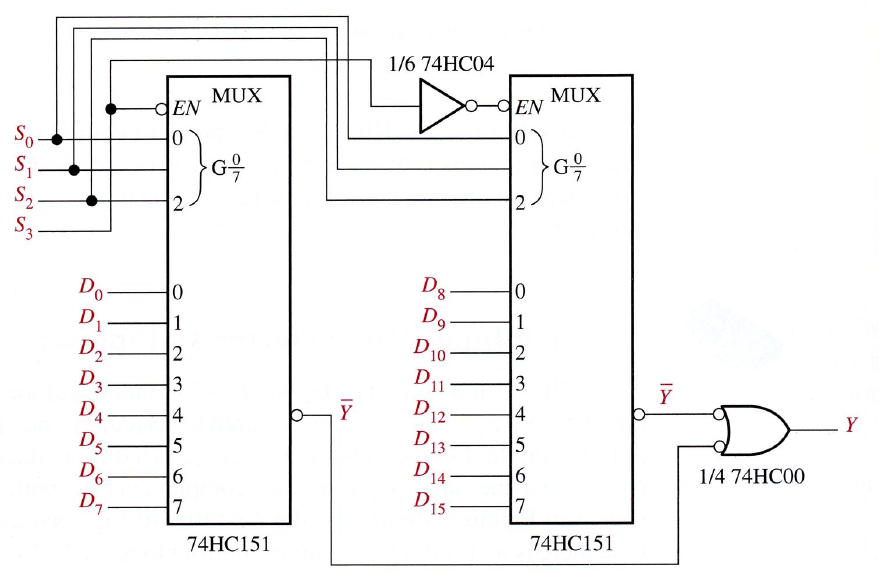
Expansion

例题

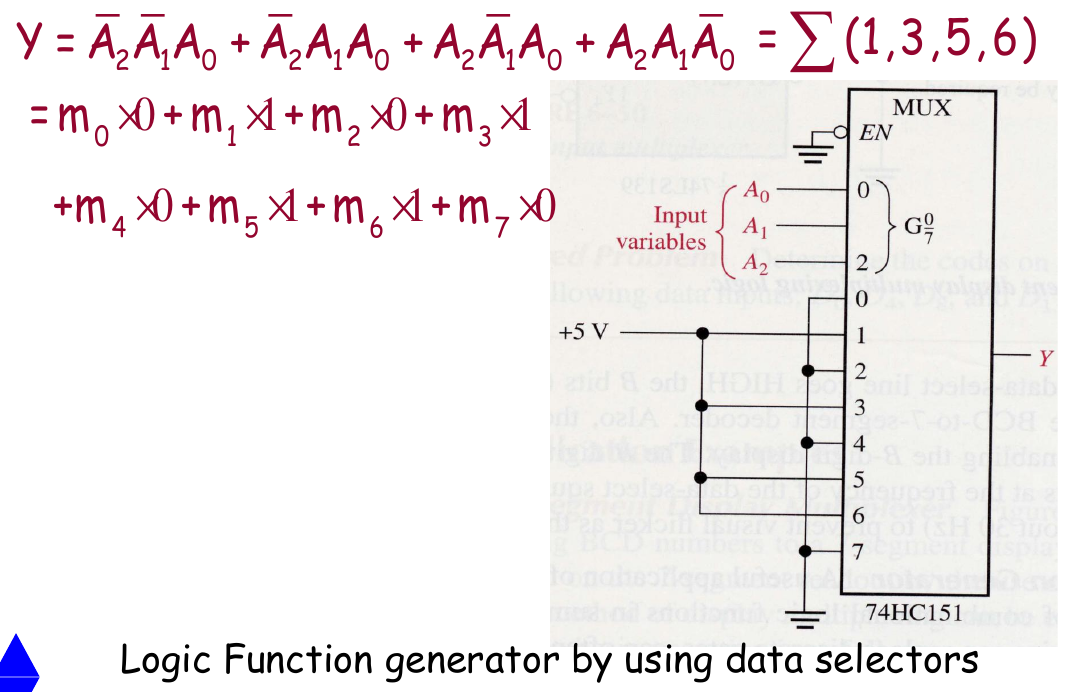
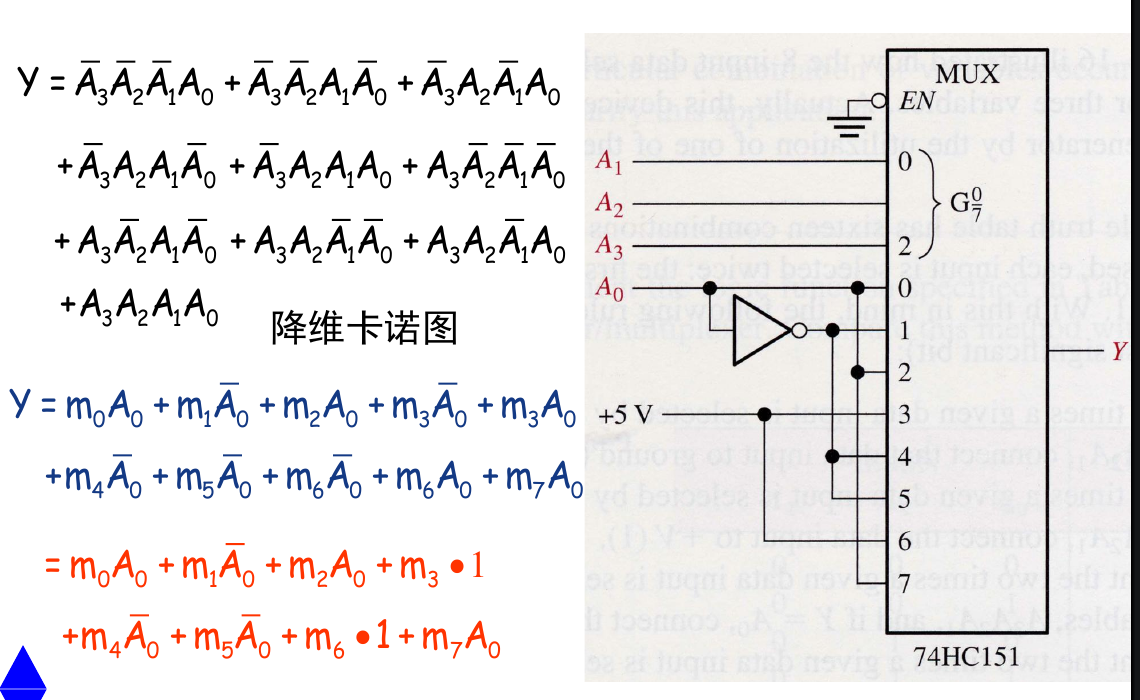
一个技巧：“降维卡诺图“。具体来说就是把三个变量作为选通用的变量（作为卡诺图的变量），剩下的一个变量作为数据输入当作常数写进卡诺图的单元格中，专门用来解下面这种题

6.7 Demultiplexers

A demultiplexer (DEMUX) basically reserves the multiplexing function. It takes data from one line and distribute them to a given number of output lines. For this reason, the demultiplexer is also known as a data distributor.

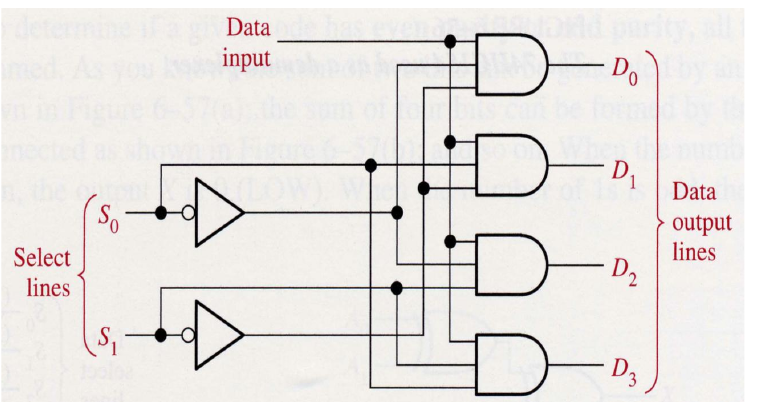
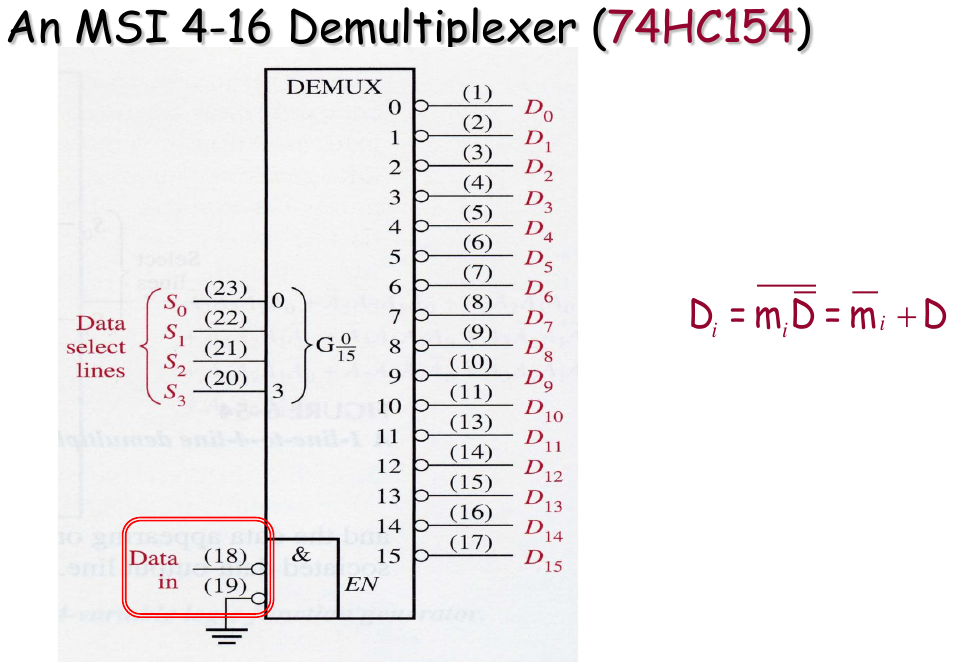
Logic Expression

$D_i = \overline{m_i \overline{D}} = \overline{m_i} + D$

6.8 Parity Generators/Checkers

Parity method uses a parity bit as a means for bit error detection.
A parity bit is attached to a group of bits to make the total number of 1s in a group always even or always odd.
Basic Parity Logic:
- The sum of an even number of 1s is always 0
- the sum of odd number of 1s is always 1

Basic Structure

Summing by XOR Gates

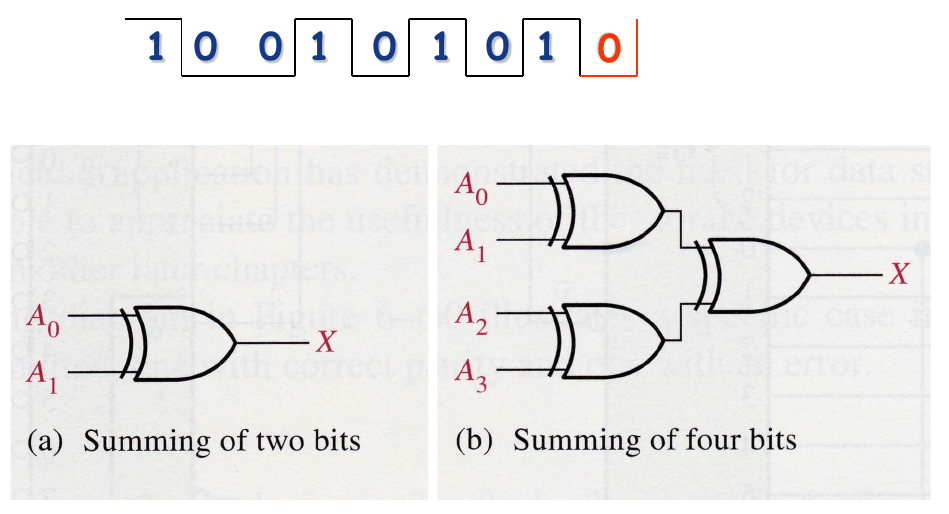
Integrated Parity Generator/Checker

Parity Checker: When the device is used as an even parity checker, the number of input bits that are highs should always be Even; and when a parity error occurs, the Even output goes LOW and the Odd goes HIGH.

Parity Generator:

For even parity generator, take Odd output as the parity bit;
For odd parity generator, take Even output as the parity bit.