Chapter10 弯曲

梁的特点

受力特点：作用于杆件上的外力都垂直于杆的轴线
变形特点：杆轴线由直线变为一条曲线
梁主要产生弯曲变形

平面弯曲的概念

常见梁的截面形状

对称弯曲：作用于杆件上的外力都垂直于杆的轴线，且都在纵向对称平面内

平面弯曲：杆发生变形弯曲后，轴线仍然和外力在同一平面内

弯曲变形的轴线——挠曲轴（线）

梁的计算简图

构件本身的简化：通常以梁的轴线来代替梁

载荷简化：作用于梁上的载荷（包括支座反力）可简化为三种类型

支座简化

3种常见支座：固定铰支座，可动铰支座，固定端

梁的种类

静定梁——支座反力

简支梁
悬臂梁
外伸梁
静定组合梁

静不定梁

10-2 剪力和弯矩

基本分析方法仍然是截面法

剪力及弯矩的方向正负号判断

内力正负号规则：同一位置处左右截面上内力分量必须具有相同的正负号

剪力 $F_s$

对脱离体内一点产生顺时针力矩的剪力为正，反之为负

更直观的记法：左上右下，剪力为正

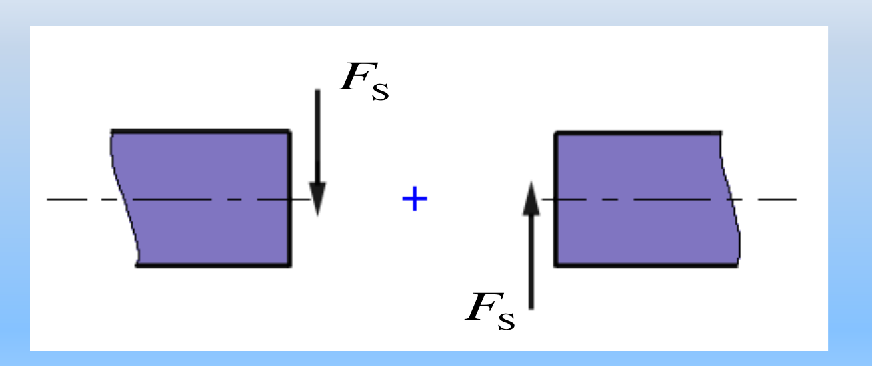
弯矩 $M$

使梁弯曲呈凹形的弯矩为正，反之则为负

更直观的记法：左顺或右逆，弯矩为正

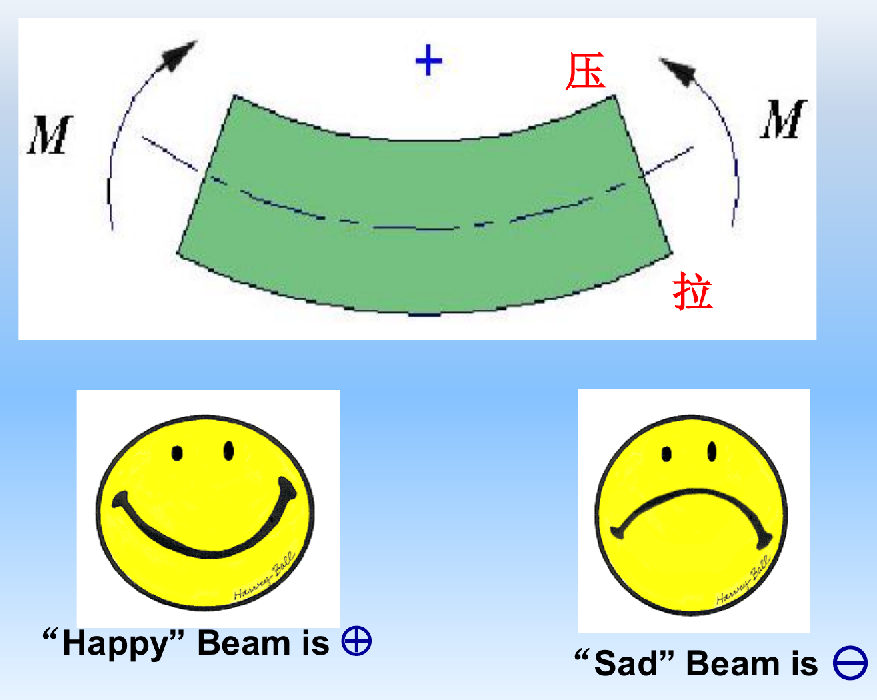
特定截面上剪力和弯矩的规律

某一截面上的内力与作用在该截面一侧局部杆件上的外力相平衡

剪力

$F_s$ = 截面一侧所有横向外力代数和

$F_s = \sum F_{i\,\text{left}} \, \text{or} \, F_s = \sum F_{i\,\text{right}}$

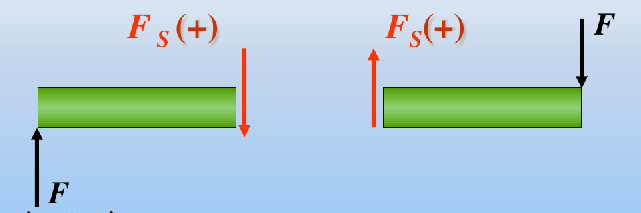
方向判断
- 外力绕该截面顺时针转向取正，逆时针转向取负
- 简便记法：左上右下是正
作用在梁上的力偶对剪力没有影响

力偶

$M$ = 截面一侧所有弯矩的代数和

$M = \sum M_{c\,\text{left}} \, \text{or} \, M = \sum M_{c\,\text{right}}$

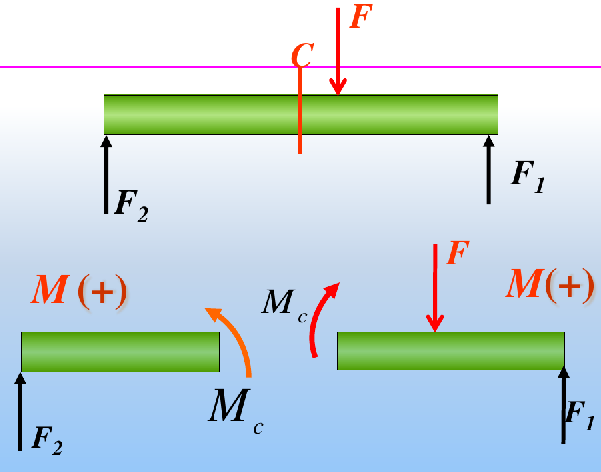
方向判断：左顺右逆时M取正，反之取负

截面上的规律

取微段分析容易得到下面的结论：

在有集中力作用的截面处，剪力有突变，弯矩无变化
在有集中力偶作用的截面处，剪力无变化，弯矩有突变

10-3 剪力方程和弯矩方程

$F_s = F_s (x) \quad M = M(x)$

分段点

大部分稍微复杂一点的情况不能用一个函数表达，那就要分段表达

各段的分界点为外力规律发生变化的截面，包括：

集中力、集中力偶作用点
分布载荷的起点和终点处的横截面

剪力图和弯矩图

用图示方法形象地表示剪力和弯矩沿梁轴线的变化情况

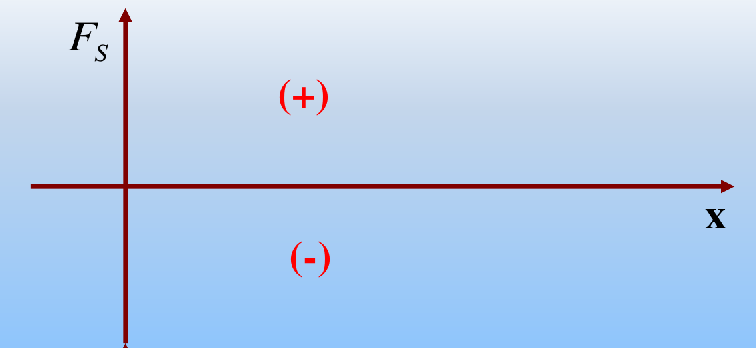
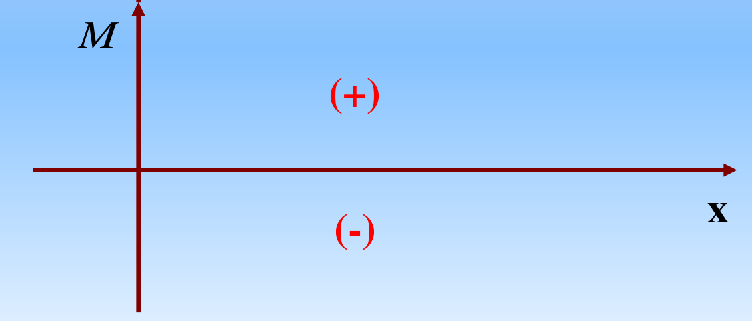
注意：必须标明控制截面（各段的分界点）上的内力值

在列梁的剪力方程和弯矩方程时，参数x可以从坐标原点算起，也可从另外的点算起，仅需要写清楚方程的适用范围（x的区间）即可。
剪力、弯矩方程的适用范围，在集中力（包括支座反力）作用处， $F _S(x)$ 应为开区间，因在该处剪力图有突变；而在集中力偶作用处， $M(x)$ 应为开区间，因在该处弯矩图有突变。
若所得方程为 $x$ 的二次或二次以上方程时，则在作图时除计算控制截面的值外，应注意曲线的凹凸向及其极值。

10-4 弯矩、剪力和分布荷载集度之间的关系

剪力与载荷集度的关系

$\frac{d F_S(x)}{dx} = q(x)$

由此式知：剪力图曲线上一点处的斜率等于梁上相应点处的载荷集度 $q$

弯矩与剪力的关系

$\frac{d M(x)}{dx} = F_S(x)$

由此式知：弯矩图曲线上一点的斜率等于梁上相应截面处的剪力 $F_S$

很容易进一步推导出

$\frac{d^2 M(x)}{dx^2} = q(x)$

弯矩图曲线上某点处的凹凸方向由梁上相应点处的载荷集度q的符号决定

总结

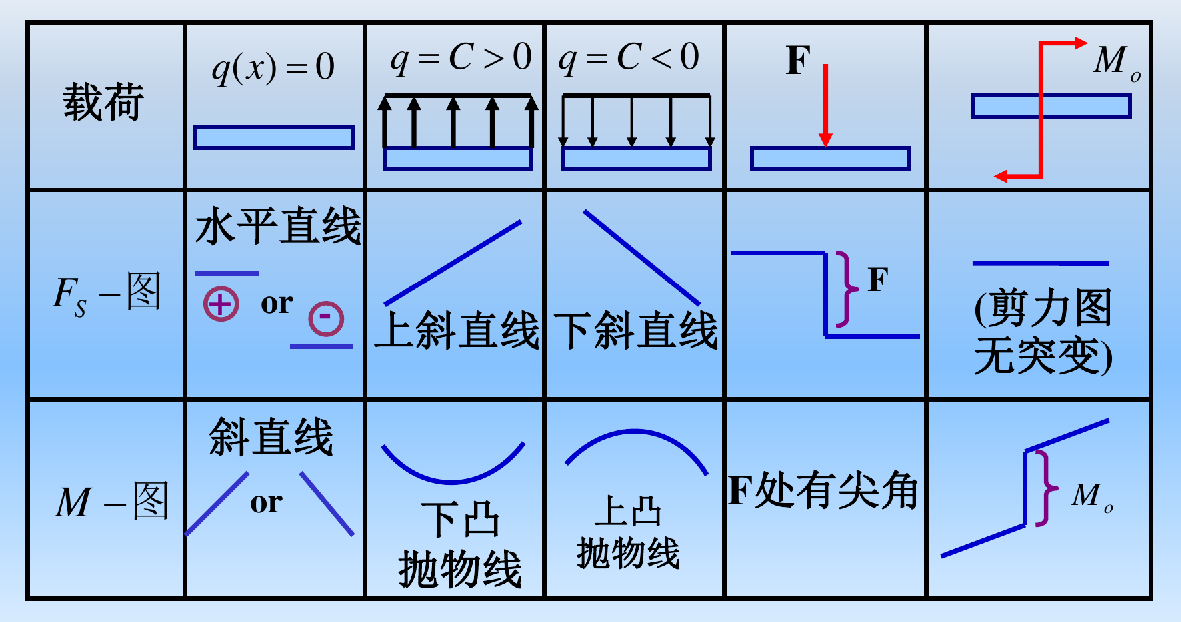
画剪力图和弯矩图的方法

列方程再画图（不太用）

根据平衡条件求支座反力
用截面上内力规律，写出梁的剪力方程和弯矩方程
作剪力图和弯矩图

根据剪力弯矩关系直接画图（快，一般用这种方法）

根据平衡条件求支座反力
- 无关方向（很多情况下水平方向）的力可以直接省略掉，进一步简化
由微分关系判断各段的 $F_s, M$ 形状
画剪力图 $F_s$ $F_{s}$
- 除了根据前面的判断画图，还要计算并标出关键点数值！
- 关键点包括截面/分段点上的值
画弯矩图 $M$ $M$
- 除了根据前面的判断画图，还要计算并标出关键点数值！
- 关键点包括截面/分段点上的值，二次曲线极值（如果有的话）