Chapter11 弯曲应力
11-1 纯弯曲时梁横截面上的应力
纯弯曲:梁弯曲变形时,横截面上只有弯曲而无剪力
横力弯曲(剪切弯曲):横截面上既有弯矩又有剪力
前提假设
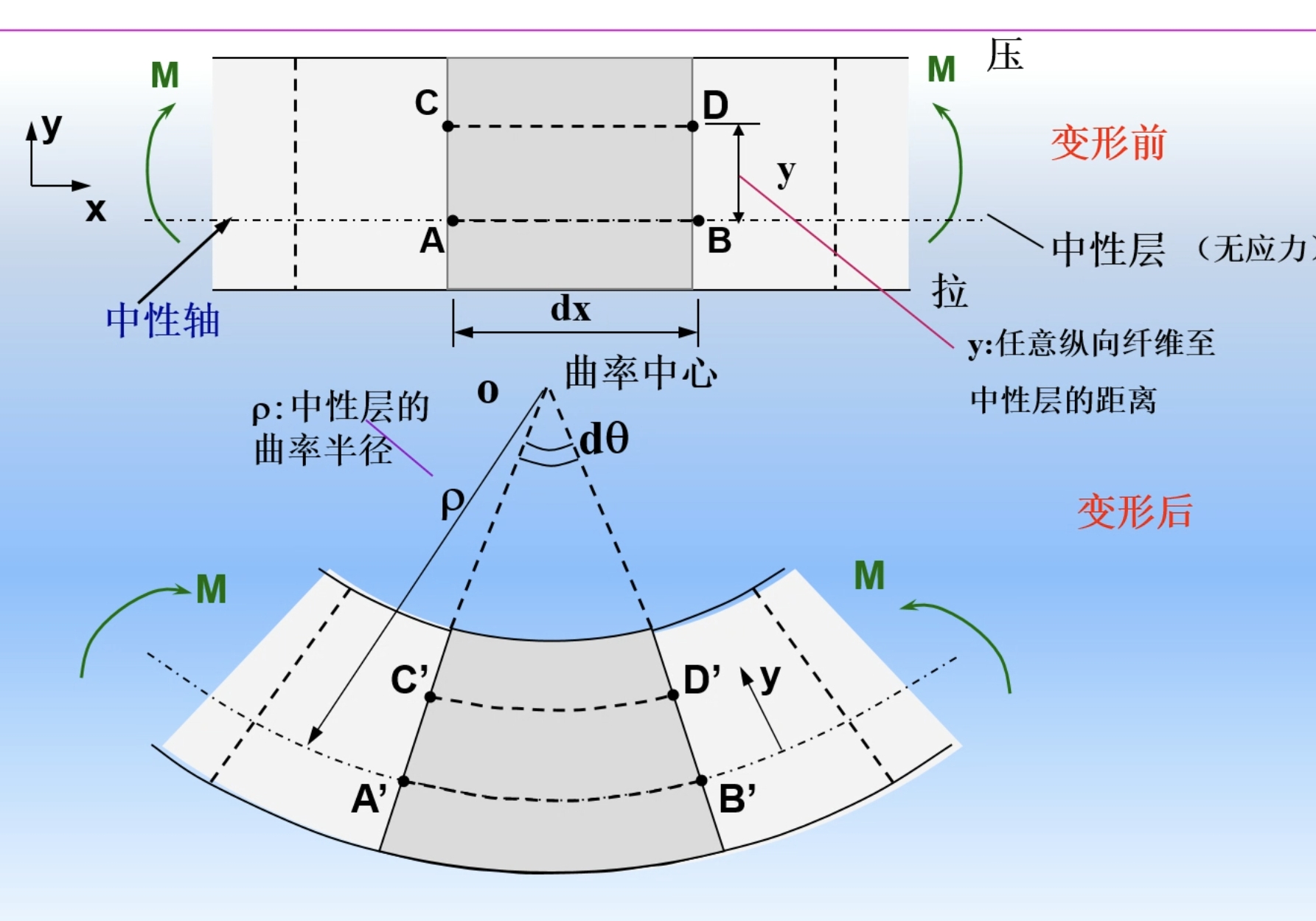
平面截面假设:变形前为平面的梁的横截面,变形后仍为平面,只是绕某轴转动了一个角度,且仍垂直于变形后的梁轴线
纵向纤维假设:—梁是由许多纵向纤维组成的,且各纵向纤维之间无挤压。
中性层和中性轴
由于连续性假设知,从顶部到底部纵向纤维,由缩短到伸长是连续变化的。所以,其间必有一层纤
维既不伸长,也不缩短,称为中性层。
中性层是梁内部拉伸区和压缩区之间的分界线
中性层与横截面的交线,称为中性轴
变形分布规律分析
变形分布规律分析
坐标轴选取:y-对称轴 z-中性轴 x轴-梁轴向
![]()
变形前
CD=AB=dx=ρdθ
变形后
C′D′=(ρ−y)dθ
应变为
ϵx=CDC′D′−CD=dx(ρ−y)dθ−dx=−ρy
故变形分布规律为
ϵ=ρy
物理意义:横截面上某点的纵向应变与该点到中性轴的距离成正比
- 当y=0时,ϵ=0
- 当∣y∣=ymax时,ϵ=∣ϵmax∣
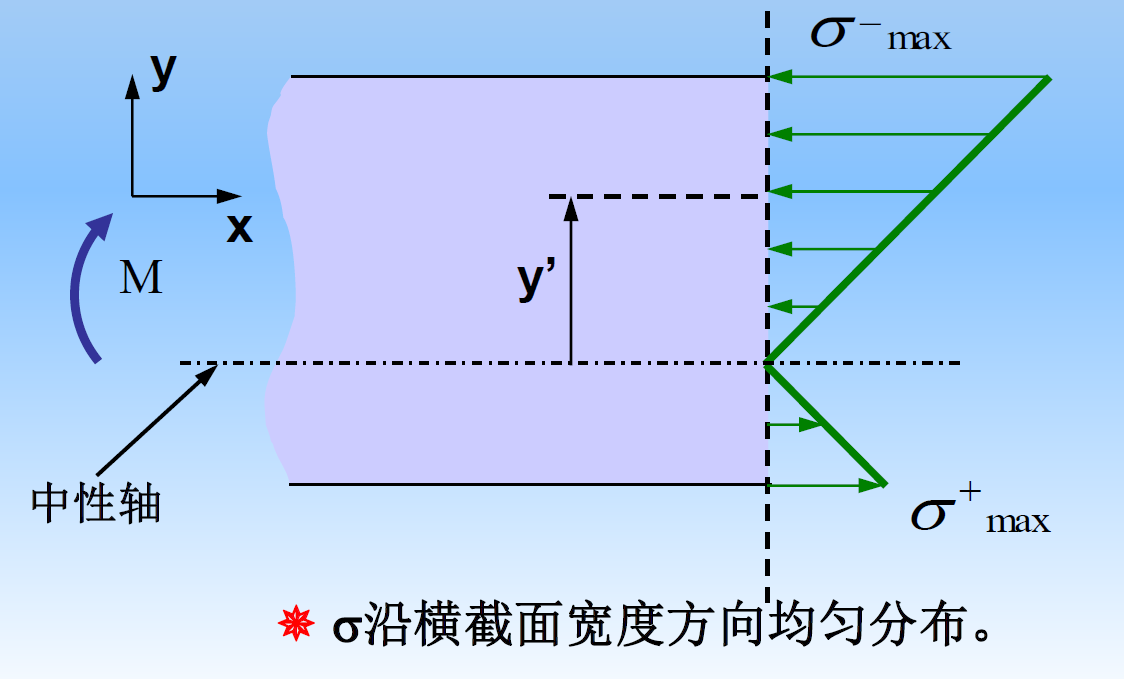
应力分布规律
在线弹性范围内,应用胡克定律
σ=Eϵ=−Eρy
对一定材料,E=C;对一定截面,ρ1=C
横截面上某点处的应力与此点距中性轴的距离y成正比
σ∝y
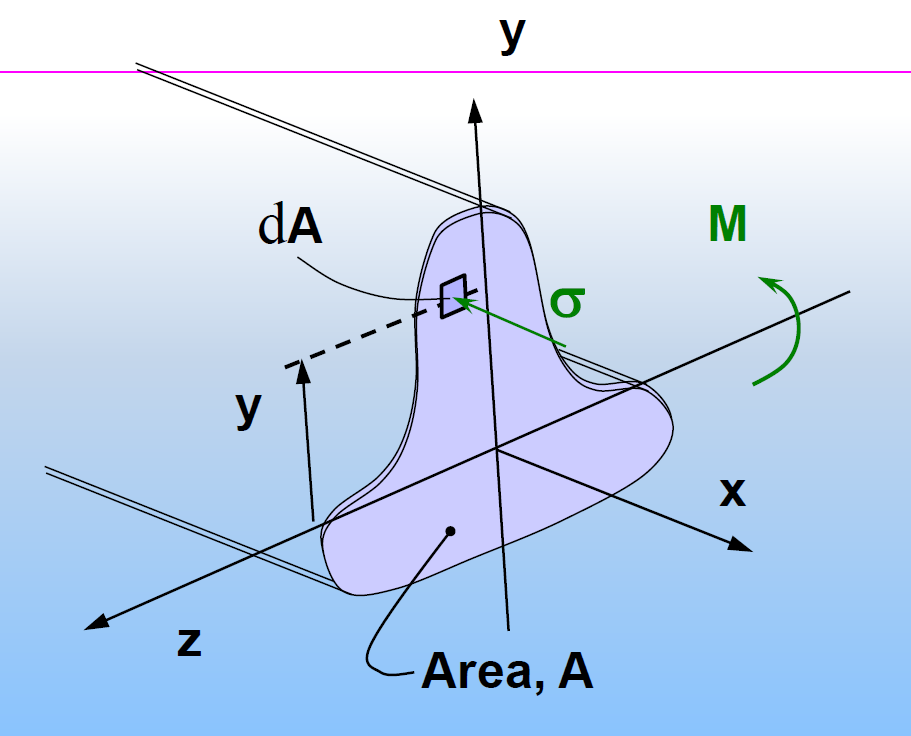
![image-20241201125351936]()
由静力平衡方程确定中性轴的位置
由∑Fx=0确定中性轴位置
坐标轴选取与前面一致:y-对称轴 z-中性轴 x轴-梁轴向
![image-20241201125850886]()
先考虑力的平衡条件
∫AσdA=∑Fx=0
代入应力分布规律
∫AρEydA=ρE∫AydA=0⟹∫AydA=0
又根据形心坐标的定义
yC=A∫AydA⟹∫AydA=AyC⟹yC=0
可以得到中性轴通过形心,并垂直于载荷作用面
由∑My=0确定对称轴位置
再考虑力矩平衡条件
∑My=0⟹My=ρE∫AyzdA=0
定义
Iyz=def∫AyzdA=0
为惯性积(惯积)
若Iyz=0,则y,z轴称为主惯性轴(主轴)
则对称弯曲时,y轴(截面的对称轴),z轴(中性轴)为截面的形心主惯性轴
注意:若图形有一对称轴,则该对称轴自动满足Iyz=0
由静力平衡方程确定挠曲轴曲率方程
考虑平衡条件
∑Mz=M
得到
Mz=∫A(σdA)⋅y=∫AEρy2dA=ρE∫Ay2dA=M
令Iz=∫Ay2dA为截面对中性轴的惯性矩
从而得到挠曲轴(挠曲线)的曲率方程
ρ1=EIzM
其中EIz为抗弯刚度
- ρ为常数,挠曲轴是一条圆弧线
- 挠曲轴/挠曲线——弯曲变形后梁的轴线
应力分析
正应力为
σ=Eρy=EIzMEy=IzMy
当y=ymax时,切应力最大为
σmax=IzMymax=ymaxIzM
令Wz=ymaxIz为抗弯截面模量,则有
σmax=WzM
Wz反映了截面的几何形状、尺寸对强度的影响
11-2 惯性矩和平行移轴公式
简单截面惯性矩及抗弯截面模量
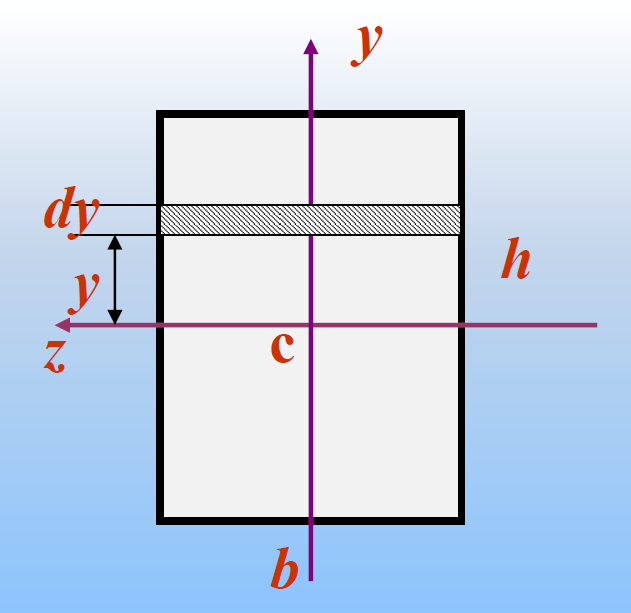
矩形
![image-20241201131227883]()
惯性矩
Iz=∫Ay2dA=∫−2h2hy2bddy=121bh3Iy=∫Az2dA=∫−2h2hz2hdz=121hb3
抗弯截面模量
Wz=ymaxIz=2h121bh3=61bh2Wy=zmaxIy=2b121hb3=61hb2
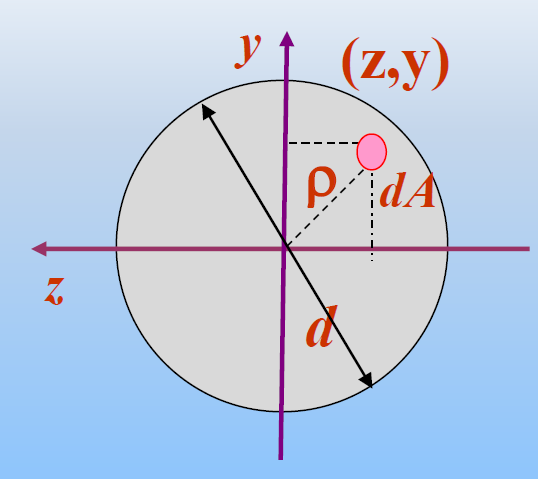
圆形
![image-20241201140104972]()
已知
IP=∫Aρ2dA=321πd4=∫A(y2+z2)dA=∫Ay2dA+∫Az2dA=Iy+Iz=321πd4
而由于对称性,易知Iy=Iz,故
Iy=Iz=21IP=641πd4
抗弯截面模量为
Wz=ymaxIz=2d641πd4=32πd3
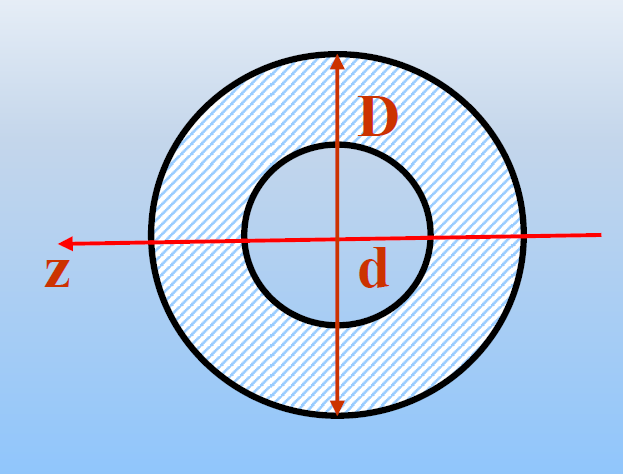
空心圆截面
![image-20241201140133500]()
Iz=21Ip=641πD4(1−α4)Wz=ymaxIz=321πD3(1−α4)
其中α=Dd为内外径比值
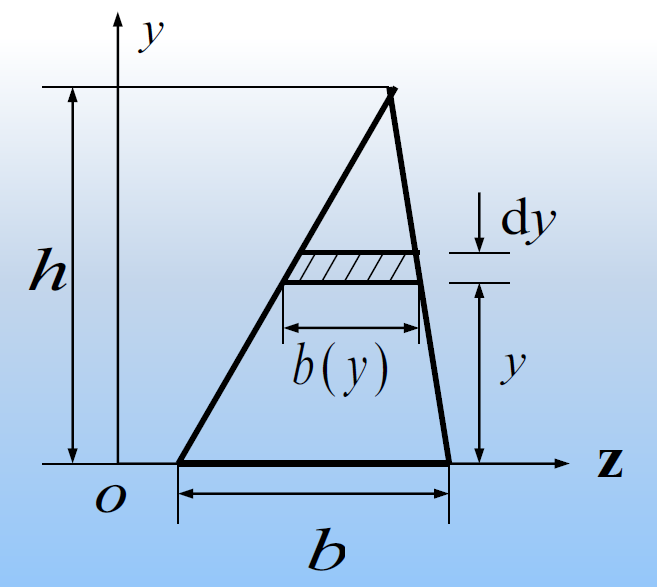
三角形
过z轴
![image-20241201140220069]()
Iz=∫Ay2dA=∫0hy2b(y)dy
由于
bb(y)=hh−y⟹b(y)=bhh−y
三角形过z轴的惯性矩
Iz=∫0hy2b(y)dy=∫0hb(1−hy)y2dy=121bh3
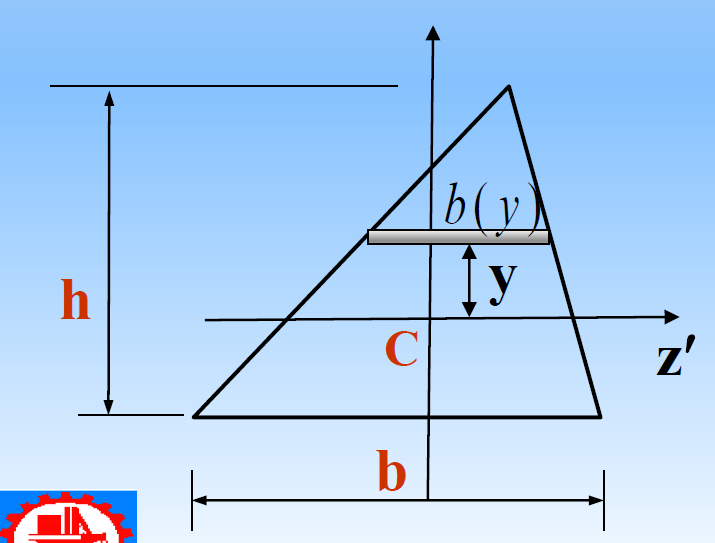
过形心C的轴
![image-20241201140249790]()
由于
bb(y)=h32h−y⟹b(y)=bh32h−y
三角形过形心C的z’轴的惯性矩
Iz=∫−3h32hy2b(y)dy=∫−3h32hb(32−hy)y2dy=361bh3
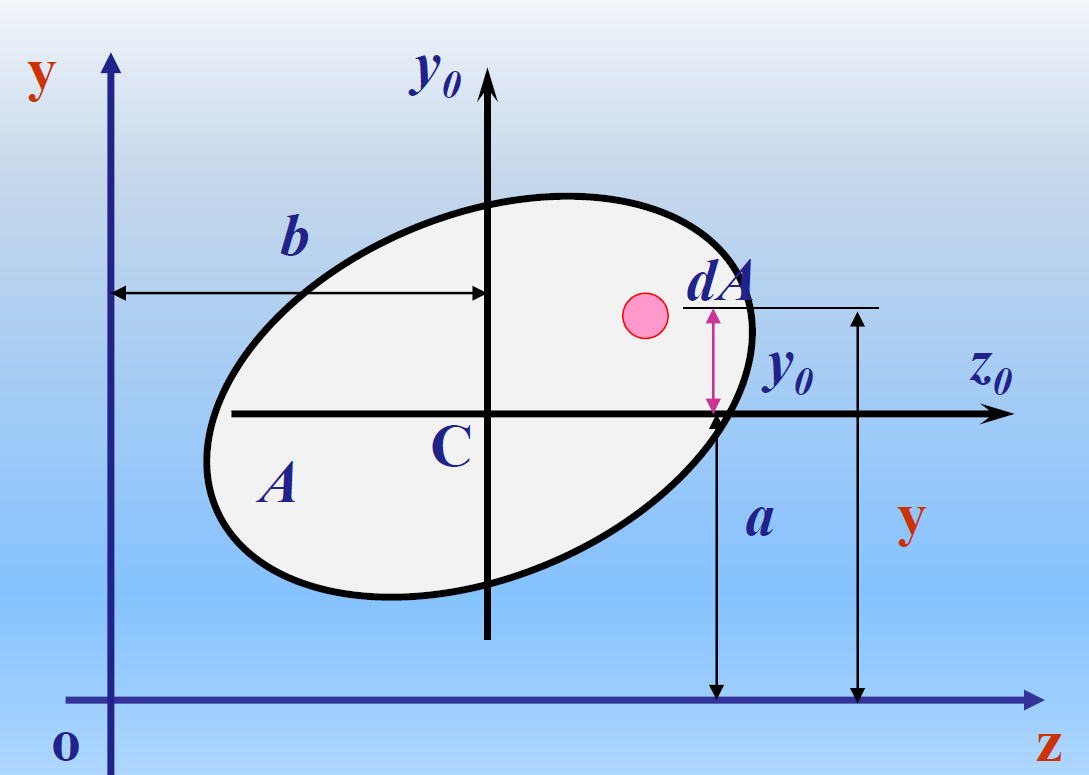
平行移轴公式
分析同一截面对于任一坐标轴z和与其平行的形心轴z0的两个惯性矩之间的关系
![image-20241201135724872]()
Iz=∫Ay2dA=∫A(y0+A)2dA=∫Ay02dA+2a∫Ay0dA+a2A=Iz0+a2A
类似地,
Iy=Iy0+Ab2
- 两平行轴中,必须有一轴为形心轴,截面对任意两平行轴的惯性矩间的关系,应通过平行的形心轴惯性矩来换算
- 截面图形对所有平行轴的惯性矩中 以对通过形心轴的惯性矩最小
组合图形的惯性矩
根据定义,整个图形对于某一轴的惯性矩等于各个分图形对同一轴的惯性矩之和
Iz=∫Ay2dA=i=1∑n∫Aiy2dA=i=1∑nIzi
11-3 横力弯曲
对于细长梁,hl>5时,横力弯曲可以近似用纯弯曲时的公式计算弯曲正应力
纯弯曲理论的推广
横力弯曲梁横截面上有剪力,因而横截面上将还有切应力存在。
弹性理论的精确分析告诉我们,这种影响与梁的跨高比hl有关,跨高比hl越大,影响越小。即梁越是细长,影响越小。
- hl>5时,横力弯曲时可近似地用纯弯曲时公式计算弯曲正应力
σ=IzM(x)y
- 对hR>5的小曲率梁,可使用直梁公式。
强度计算-弯曲正应力强度条件
σmax=WzMmax≤[σ]
注意塑形材料和脆性材料的计算是不同的
11-4 弯曲时的切应力
矩形截面梁
两个假设
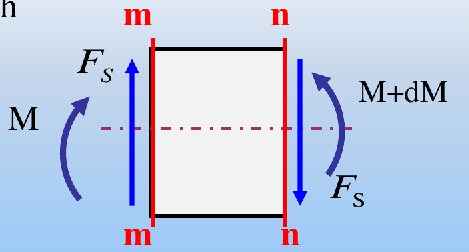
分析方法(截面法)
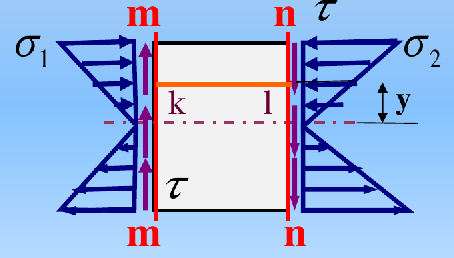
- 沿mm,nn截面截开,取微段dx
- 从微段dx上,用距中性轴为y的纵向截面,再纵向切出一段微段mnkl
![image-20241224102101741]()
![image-20241224102128215]()
![image-20241224104159131]()
代入平衡条件,计算
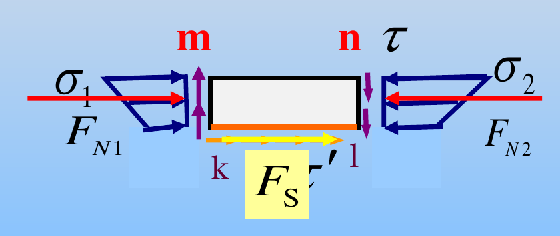
平衡条件
∑Fx=0⟹FN1+τ′(y)bdx=FN2
代入
∫A1IzMy1dA+(bdx)τ′(y)=∫A1Iz(M+dM)y1dA⟹(bdx)τ′(y)=∫A1IzdMy1dA
再根据切应力互等定理,可以得到结论
τ(y)=τ′(y)=bdxdMIz1∫A1y1dA=b⋅Iz1dxdM∫A1y1dA=b⋅IzFsSz∗
其中
-
τ 为截面上距中性轴 y 处的切应力
-
b 为 y 处的宽度
-
Iz 为整个截面对中性轴的惯性矩
-
y1dA定义为面积微元 dA 关于中性轴的静矩
-
Sz∗=∫A1y1dA 是 y1>y 的面积A1对中性轴的静矩
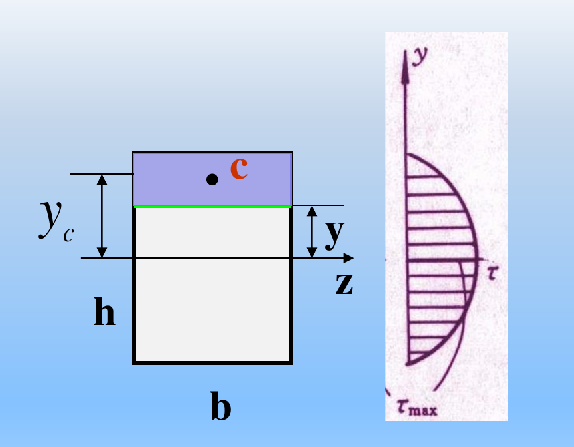
矩形的静矩
![image-20241224105005494]()
$$
\begin{aligned}
S_z^* &= \int_{A_1} y_1 \, dA = A_1 \cdot y_c' = b\left(\frac{h}{2} - y\right)\left[ y+\frac{1}{2} (\frac{h}{2} - y) \right]\\
&= \frac{b}{2} \left(\frac{h^2}{4} - y^2\right)
\end{aligned}
$$
带入切应力的公式,就可以得到
$$
\tau = \tau' = \frac{6F_s}{bh^3} \left( \frac{h^2}{4} - y^2 \right)
$$
可以发现最大值出现在
$$
y=0, \tau = \tau_{\max} = \frac{3}{2} \frac{F_s}{bh} = \frac{3}{2} \frac{F_s}{A}
$$
而在边缘,切应力为0
$$
y=\pm \frac{h}{2}, \tau = 0
$$
- 该公式做了很多近似,仅适用于狭长矩形,正方形或更扁的截面就无法使用了
正应力与切应力比较
![image-20241224110148817]()
弯曲正应力(最大值):
σmax=bh2Fl=bh26Fl
弯曲切应力(最大值):
τmax=23bhF
应力比值:
τmaxσmax=2bh3Fbh26Fl=4(hl)
当 l≫h 时,σmax≫τmax。
工字型截面梁
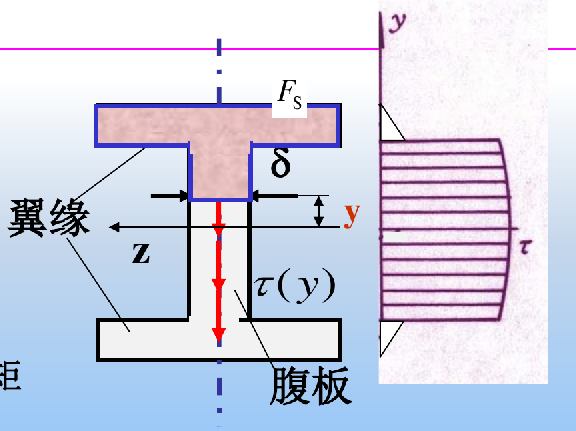
![image-20241224110552919]()
腹板
对于腹板部分,有切应力公式:
τ(y)=δIzFSSz∗
其中
- τ(y):截面上距中性轴 y 处的切应力;
- Sz∗:y 处横线一侧的部分面积对中性轴的静矩;
- Iz:整个截面对中性轴的惯性矩;
- δ:y 处的宽度。
最大切应力公式为
τmax=δIzFSSz,max
- 腹板上的切应力呈抛物线变化,腹板部分的切应力占总剪力的 95%~97%。
翼缘
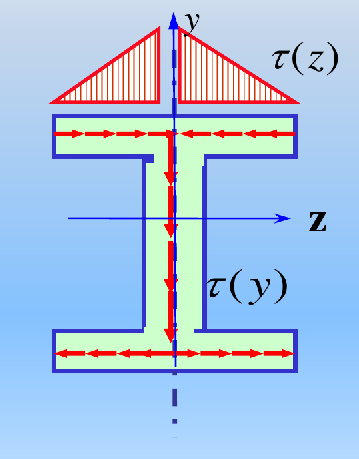
![image-20241224111138352]()
- 翼缘部分的水平切应力沿翼缘宽度按直线规律变化,并与腹板部分的竖向切应力形成“切应力流”
- 翼缘部分的切应力相比腹板上的切应力数值较小,是次要的,强度计算时一般不予考虑
- 腹板负担截面上的绝大部分剪力,翼缘负担截面上的大部分弯矩
切应力强度条件
τmax=(δIzFSSz,max)max≤[τ]
- 对于等宽度截面:τmax 发生在中性轴上;
- 对于宽度变化的截面:τmax 不一定发生在中性轴上。
对于矩形截面梁,应力比值:
τmaxσmax=4(hl)
- 故对于矩形截面梁,一般不需要校核切应力
- 当然,考试的时候看题目要求
提高弯曲强度的一些措施
- 选择合理截面,提高抗弯截面系数
- 梁一般都选择竖放而不是横放,因为竖放Wz更大
- 选择材料远离中性层的截面是更合理的
- 在中性轴附近开孔,节约材料但是对强度影响不大
- 对脆性材料,形心靠近拉边,远离压边
- 合理分布载荷的位置
- 载荷尽量靠近支座
- 将集中力分为多个分力,甚至是均布力
- 合理安排支座甚至增加支座
- 选用合理的高级结构
 $$
\begin{aligned}
S_z^* &= \int_{A_1} y_1 \, dA = A_1 \cdot y_c' = b\left(\frac{h}{2} - y\right)\left[ y+\frac{1}{2} (\frac{h}{2} - y) \right]\\
&= \frac{b}{2} \left(\frac{h^2}{4} - y^2\right)
\end{aligned}
$$
带入切应力的公式,就可以得到
$$
\tau = \tau' = \frac{6F_s}{bh^3} \left( \frac{h^2}{4} - y^2 \right)
$$
可以发现最大值出现在
$$
y=0, \tau = \tau_{\max} = \frac{3}{2} \frac{F_s}{bh} = \frac{3}{2} \frac{F_s}{A}
$$
而在边缘,切应力为0
$$
y=\pm \frac{h}{2}, \tau = 0
$$
$$
\begin{aligned}
S_z^* &= \int_{A_1} y_1 \, dA = A_1 \cdot y_c' = b\left(\frac{h}{2} - y\right)\left[ y+\frac{1}{2} (\frac{h}{2} - y) \right]\\
&= \frac{b}{2} \left(\frac{h^2}{4} - y^2\right)
\end{aligned}
$$
带入切应力的公式,就可以得到
$$
\tau = \tau' = \frac{6F_s}{bh^3} \left( \frac{h^2}{4} - y^2 \right)
$$
可以发现最大值出现在
$$
y=0, \tau = \tau_{\max} = \frac{3}{2} \frac{F_s}{bh} = \frac{3}{2} \frac{F_s}{A}
$$
而在边缘,切应力为0
$$
y=\pm \frac{h}{2}, \tau = 0
$$