Chapter8 轴向拉伸与压缩
8-2 轴力与轴力图
- 横截面上的内力:轴力
- 分析方法:截面法
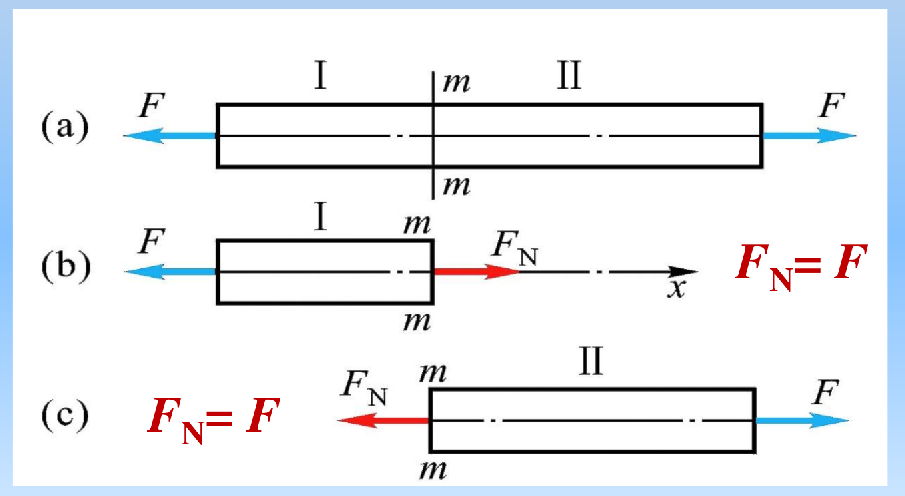
截面法
- 截开
- 取一段
- 加内力
- 平衡
![image-20241222141745337]()
轴力正负号:以拉为正,以压为负
- FN与截面外法向同向,为正轴力(拉力)
- FN与截面外法向反向,为负轴力(压力)
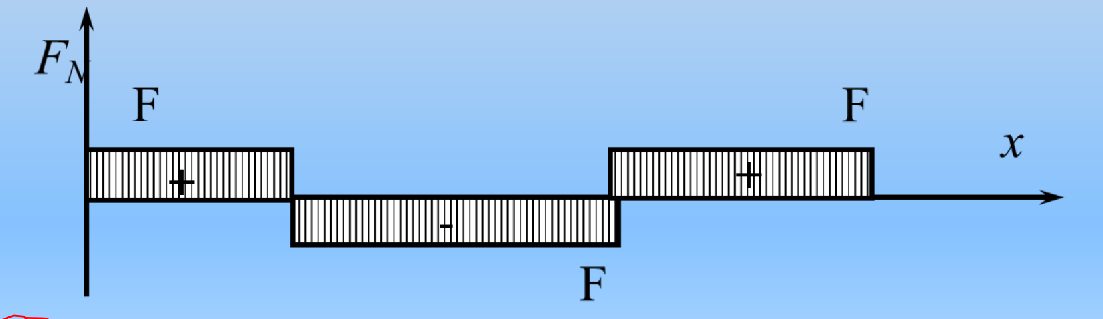
轴力图
轴力沿轴线变化的图形
- 横坐标标轴x平行于轴件轴线,表示横截面位置
- 纵坐标标轴F表示相应横截面的轴力值。
- 如轴力为拉力,则画在x轴上方,轴力为压力,则画在x轴下方
- 轴力图中需标明(+)、(-)以表示拉压。
![image-20241222141937904]()
- 反映出轴力沿轴线方向变化关系,较直观
- 轴力图可以方便确定最大轴力的数值及其横截面所在的位置,方便确定危险截面
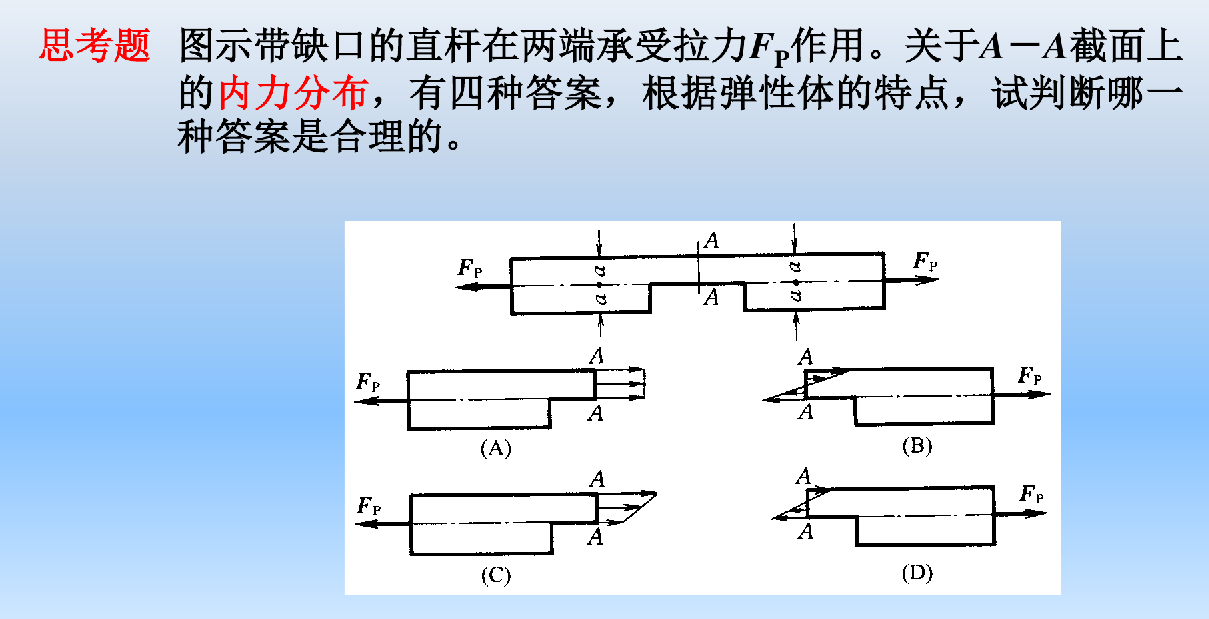
![image-20241222143800157]()
答案:D
A B的轴力合成以后要么只有合力,要么只有合力矩,显然是错的
C的合力矩方向错误,D正确
应力
分布内力在截面内一点的密集程度
截面上M点的应力
点M-截面上一点
ΔA 围绕M点的微小区域面积
ΔFR ΔA区域内的内力合力
p=ΔAΔFR
称之为区域内的平均应力
取极限,就称为M点的合应力
p=ΔA→0limΔAΔFR
进行分解
得到正应力-垂直于截面的应力
σ=ΔA→0limΔAΔFN
切应力-平行于截面的应力
τ=ΔA→0limΔAΔFS
应力的特点:
- 应力是矢量
- 同一横截面上,不同点处的应力一般不同
- 过同一点,不同方位截面上的应力一般不同
- 整个截面上的各点处的应力与微面积ΔA乘积的合成,即为该截面上的内力
8-3 拉压杆的应力
横截面上的应力
正应力公式
σ=AFn
正负号规定:拉应力为正,压应力为负
拓展:
- 若轴力沿轴线变化,则FN=FN(x)
- 对边界面杆,当截面变化缓慢时,外力合力与轴线重合,横截面上的正应力也近似为均匀分布
适用条件
- 外力的合力作用线必须与杆件轴线重合
- 不适用于集中力作用点附近的区域
圣维南原理
应力公式的适用条件说明:公式不适用于集中力作用点附近的区域,因为该区域横截面上的应力是非均匀分布的,随着加载方式的不同,加载点附近的应力分布方式会发生变化。
加力方式(静力等效的力系)不同,只对力作用点附近区域的应力分布有显著影响,而在距力作用点稍远处,应力都趋于均匀分布,其影响范围不超过一个横向尺寸,即圣维南原理。
局部影响原理
圣维南原理的等价提法:如果作用在弹性体某一小块面积(或体积)上的荷载的合力和合力矩都等于零,则在远离荷载作用区的地方,应力就小得几乎等于零。
斜截面上的应力
- 内力确定-截面法
- 应力确定
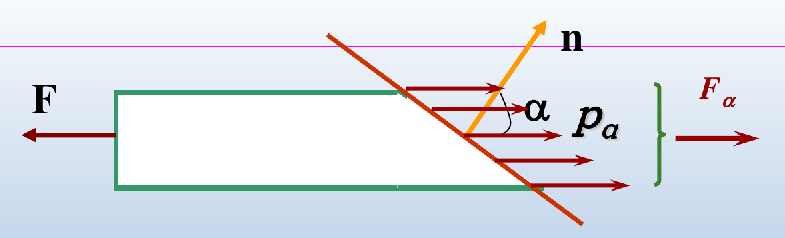
实验证明:斜截面上既有正应力,又有切应力,且应力分布均匀
![image-20241027195306104]()
设横截面上应力为σ
斜截面上的合应力为
pα=aαFα=AFcosα=σcosα
正应力
σα=pαcosα=σcos2α=2σ(1+cos2α)
切应力
τα=pαcosα=σcosαsinα=2σsin2α
其中正负号规定为
- σ 拉正,压负
- τ 对分离体内一点产生顺时针力矩的切应力为正,反之为负
- α 横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负
讨论:
- 当α=0时,(σα)max=σ 横截面上存在最大正应力
- 当α=90∘ (σα)min=0,τα=0,即纵截面上的应力为0,因此在纵截面不会被破坏
- 当α=±45∘时,σα=2σ,∣τα∣=2σ,即与杆件成45∘的斜截面上切应力达到最大值,而正应力不为0
- 由τα=21σsin2α,得τα=−τα+90∘
8-4 拉(压)时的强度计算
强度失效的基本形式
- 塑性屈服
- 脆性断裂
极限应力
杆件中的应力随着外力的增加而增加,当达到一定极限时,材料会发生破坏,此极限值称为极限应力或危险应力,以σ∘表示
塑性材料的极限应力
σ∘=σs
脆性材料的极限应力
σ∘=σb
许用应力与安全因数
引入安全因数n,定义
nσ∘=[σ]
[σ]为材料的许用应力
强度条件
AFNmax=σmax≤[σ]=nσ∘
解决的几类问题
-
设计截面尺寸:已知FNmax,[σ],求A
A≥[σ]FNmax
-
确定许可载荷:已知A,[σ],求FNmax
FNmax≤A[σ]
-
强度校核:都确定好了,看一看符不符合强度条件
σmax=AFNmax(<or=or>)[σ]
解题一般步骤
- 由实际问题抽象出力学模型
- 受力分析
- 内力
- 应力
- 利用强度条件校核强度
8-5 轴向拉(压)时的变形
拉伸:纵向伸长,横向缩短
压缩:纵向缩短,横向伸长
拉压杆纵向变形和横向变形计算
横向/纵向绝对变形
Δl=l1−lΔb=b1−b
横向/纵向线应变
ϵ=lΔl=ll1−lϵ′=bΔb=bb1−b
纵向线应变和横向线应变的关系(泊松比)
当应力小于比例极限时,横向应变与纵向应变之比为一常数μ,称为横向变形系数(泊松比)
μ=∣ϵϵ′∣ϵ′=−μϵ
泊松比是材料的弹性常数
大部分材料的泊松比是正值,并且0<μ<0.5
拉压杆的弹性定律(胡克定律)
在弹性范围内(σ≤σp),杆的伸长(缩短)与外力F、杆长l成正比,而与横截面积A成反比,即
Δl∝AFl
引入比例常数E(杨氏模量),则
Δl=EAFl=EAFNl
E为弹性模量(杨氏模量),是表示材料弹性性质的一个系数
EA为杆的抗拉(或抗压)刚度,反映杆件抵抗变形的能力,抗拉刚度越大,杆件越不易变形
对式子进行变形
ϵ=lΔl=EAFN=Eσ
即可得到应力,应变关系(弹性定律/胡克定律)
ϵ=Eσ
用应力应变表示的胡克定律表明,在弹性范围内,杆件上任意点的应力与应变成正比
拉压杆变形的计算
-
等轴力等截面拉压杆:直接套公式
Δl=EAFNl
-
阶梯杆:分段计算总变形
- 各段E同,A不同,轴力FN在各段中分别为常量,分别计算每段变形,加起来得到总变形
Δl=i∑Δli=i=1∑nEiAiFNili
-
(连续)变内力变截面:积分求解
Δl=∫ld(Δl)=∫lEAFN(x)dxor∫lEA(x)FNdx
或者,更一般的情况,FN,E和A都是是变化量的话
Δl=∫lE(x)A(x)FN(x)dx
使用了载荷的叠加原理,适用条件
- 弹性变形
- 载荷与变形成线性关系
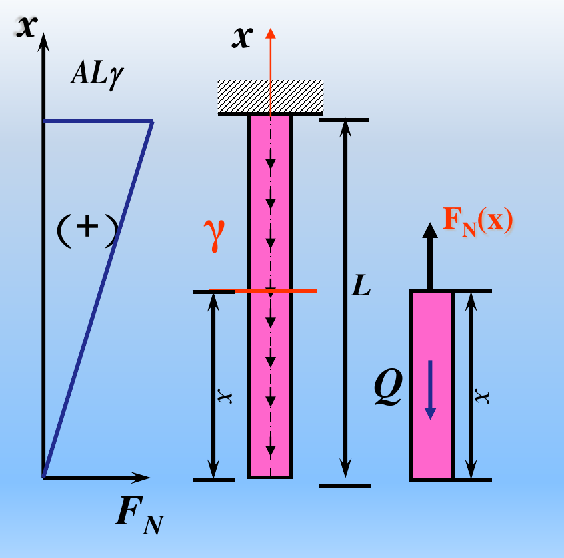
【例题2-3】求自由悬挂的等直杆由于自重引起的最大正应力和总伸长。设杆的长度L、截面面积A,比重为γ,弹性模量E均为已知。
![image-20241222160615935]()
解题方法:
- 计算轴力,画出杆的轴力图
q=LγAL=γAFN(x)=qx=γAxΔl=∫ld(Δl)=∫0lEAγAxdx
-
计算杆内最大正应力
FN(x)=Ax⋅γFNmax=AL⋅γσx=AFNx=AAx⋅γ=x⋅γσmax=γL
-
杆的伸长量
Δl=∫0lEAFN(x)dx=∫0lEAγAxdx=2Eγl2
桁架的节点位移
桁架的变形一般以桁架的节点位移来表示
下面以一道例题来说明如何处理这类问题
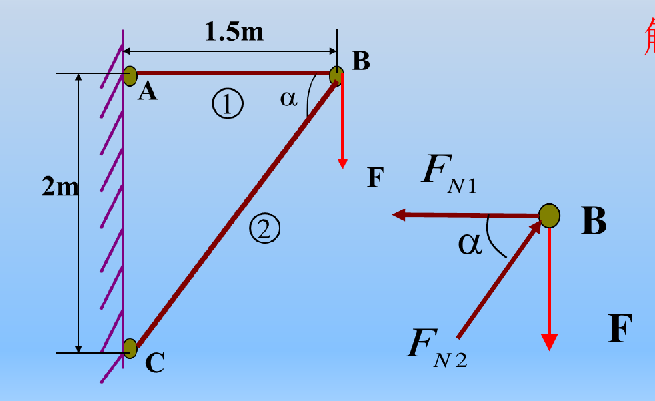
例题2.4 如图所示的桁架结构中,杆件1和杆件2的材料和截面属性分别如下:
- 杆件1:
- 圆形截面,直径 d=16 mm,弹性模量 E1=2×105 MPa
- 杆件2:
- 方形截面,边长 a=100 mm,弹性模量 E2=10 GPa
已知外力 F=19.6 kN,连接点 A、B 和 C 可视为铰接。要求计算 B 点的水平位移 ΔH 和竖直位移 ΔV。
![image-20241222163317994]()
-
内力计算
根据静力平衡条件列方程:
F=FN2sinαFN1=FN2cosα
解得:
FN1=43F(拉力),FN2=45F(压力)
- 计算杆件变形
根据杆件的轴向变形公式:
Δl=EAFNl
-
对杆件1:
Δl1=E1A1FN1l1=0.5223 mm
-
对杆件2:
Δl2=E2A2FN2l2=0.612 mm
-
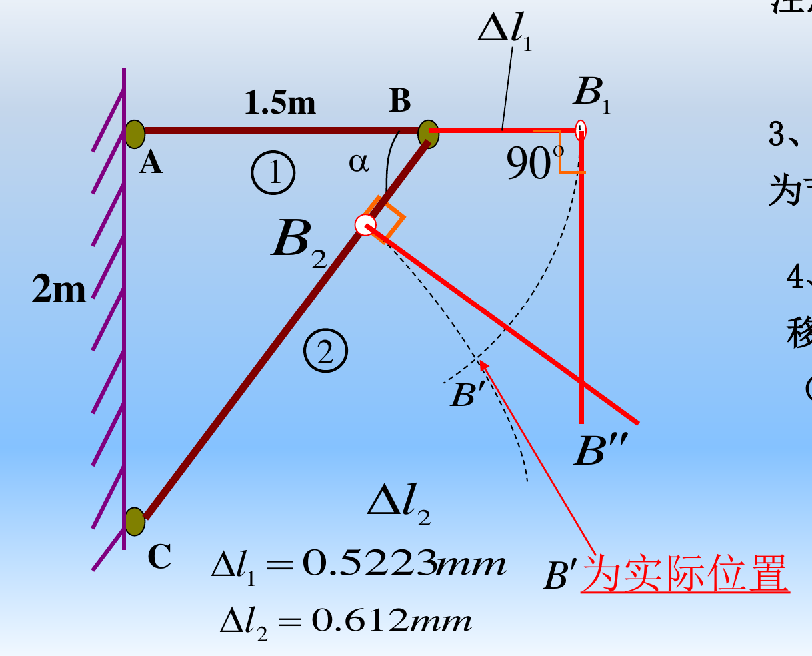
绘制变形图:沿杆件变形方向绘制变形,再采用近似方法绘制节点B变形后位置B′′
![image-20241222163946582]()
-
如何确定B点的新位置?
-
以A为圆心,Δl1+l1为半径,作圆弧
-
以C为圆心,Δl2+l2为半径,作圆弧
-
交点是B点的新位置B′
-
用以上这种方法很麻烦,而且难以计算,所以要采用近似方法
- 沿杆件变形方向绘制变形,并注意拉力导致杆件伸长,压力导致杆件缩短。将变形后的节点位置分别标记为 B1 和 B2
- 过B1和B2点做垂线(以垂线替代圆弧),交点即为节点B的新位置B′′
-
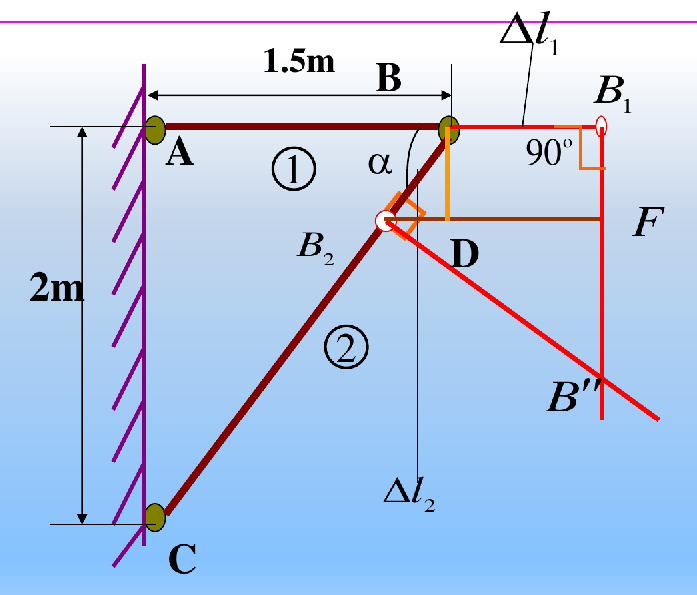
根据画出的变形图,根据几何关系计算 B 点水平位移和竖直位移
![image-20241222163836240]()
ΔV=B′′B1=BD+B′′F=Δl2sinα+tanαΔl1+Δl2cosα=sinαΔl2+tanαΔl1=1.157 mm
近似替代方法总结
-
由于是小变形,所以圆弧可以近似以垂线代替
-
以垂线代替圆弧,交点即为节点新位置
-
根据几何关系求出水平位移和垂直位移
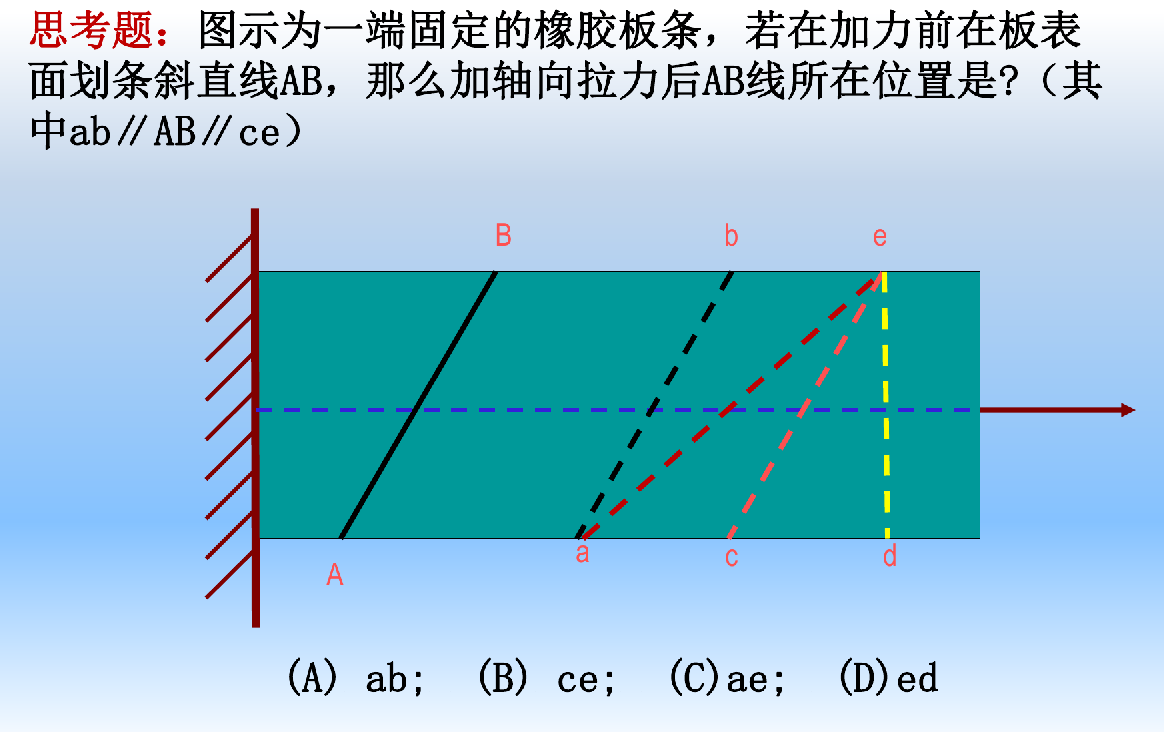
思考题
答案:应该是ae
![image-20241222171342663]()
8-6 材料的力学性能
8-7 应力集中
应力集中现象
由于构件截面突然变化导致局部应力发生骤然变化的现象称为应力集中现象
引力集中因数
K=σ0σmax
其中σmax为局部最大应力,σ0为削弱处的平均应力
引力集中因数K>1
材料的影响
静载荷作用下
- 应力集中对塑性材料的影响不大:因为有屈服极限
- 应力集中对脆性材料的影响较为严重
动载荷作用下
需要考虑金属疲劳的影响
8-8 简单拉压静不定问题
作用在杆件上的外力或杆件横截面上的内力,都能够由静力平衡方程直接确定,这类问题称为静定问题。
未知力个数>平衡方程数,是无法仅靠静力平衡方程是无法确定全部未知力,这类问题就是超静定问题或静不定问题
静不定次数=未知力个数-独立平衡方程数
静不定解法
在平衡方程以外,寻找补充方程,且补充方程数目等于静不定次数
建立补充方程的关键:根据变形协调条件(各构件之间变形的集合关系)建立变形几何方程(变形协调方程),再由物理方程(胡克定律)得到补充方程
- 平衡方程
- 根据变形协调条件,写出变形几何方程:
- 绘制变形图,确定变形点的变形位置,然后根据得到几何约束关系
- 如果有多个变形杆,可以先根据其中两杆的变形确定变形点,然后得到所有杆的几何约束关系
- 将物理条件(物理方程/胡克定律)代入变形约束条件(变形几何方程),即得补充方程
- 通过方程组解出所有未知力
常见的变形约束关系
- 画变形图,从图中找几何关系
- 固定端位置不变,例如:
- 两端固定的杆子总长度不变
- 连接到同一垂直杆上的平行轴伸长量之间的比例关系
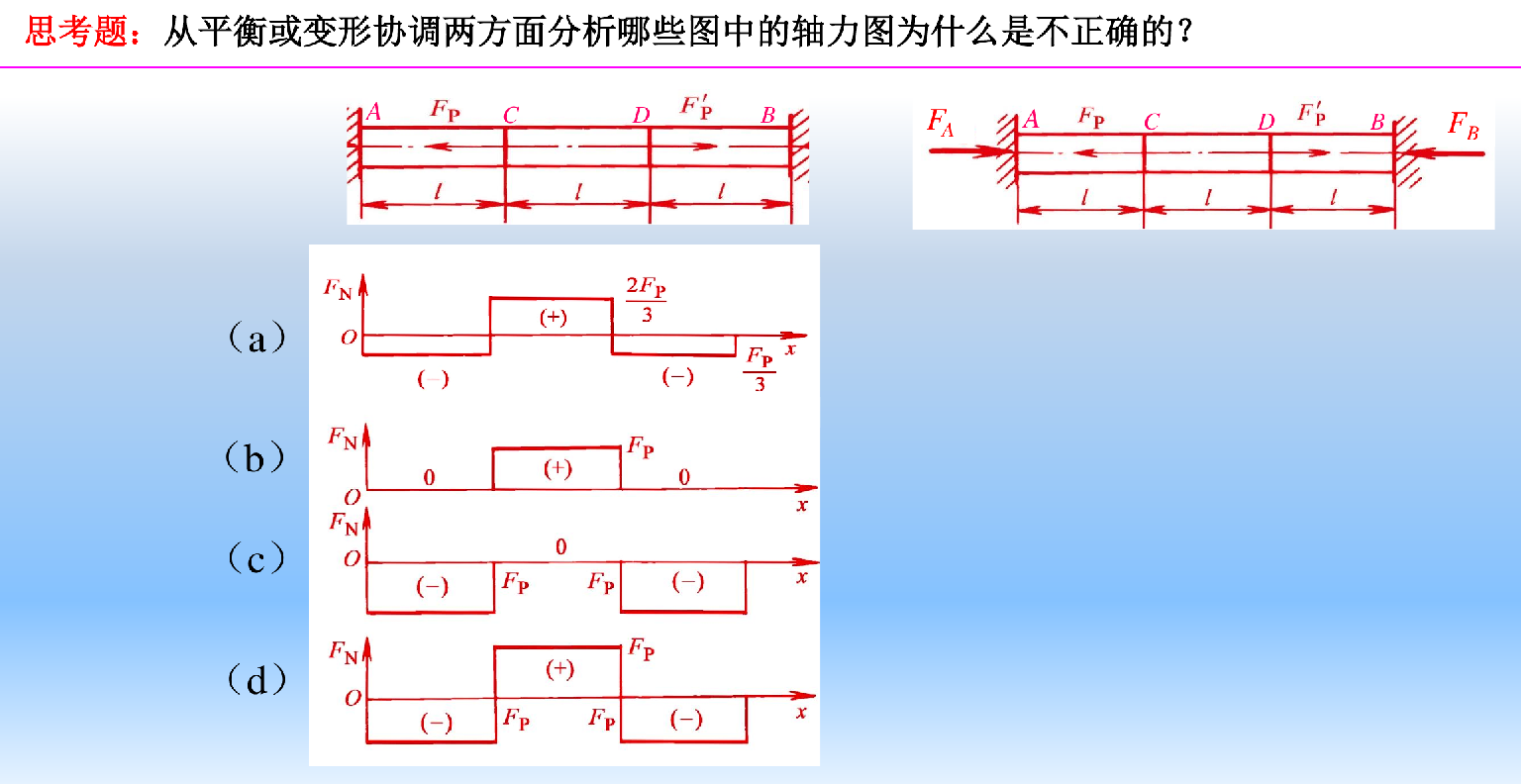
![image-20241222200329416]()
答案:a是正确的,其他都是错误的,直接从变形协调条件就能判断
其他技巧
- 省略静力平衡方程的技巧:如果有n个未知力并不想求,静力平衡方程可以相应省略n个,但是注意保留的静力平衡方程要只包含待求的力,例如如果有两个未知力不想求,可以省略2个静力平衡方程,但是剩下的方程要只包含待求的力
“能者多劳”
温度应力
温度引起的变形量
ΔL=αΔtL
α为材料线膨胀系数,Δt为温度变化量,L为杆件的初始长度
![]()
Δl=ΔlT+ΔlF
其中
ΔlT=αlΔtlΔlF=−EAFl
代入计算,得
F=αlΔtEA⟹σ=AF=αlEΔt
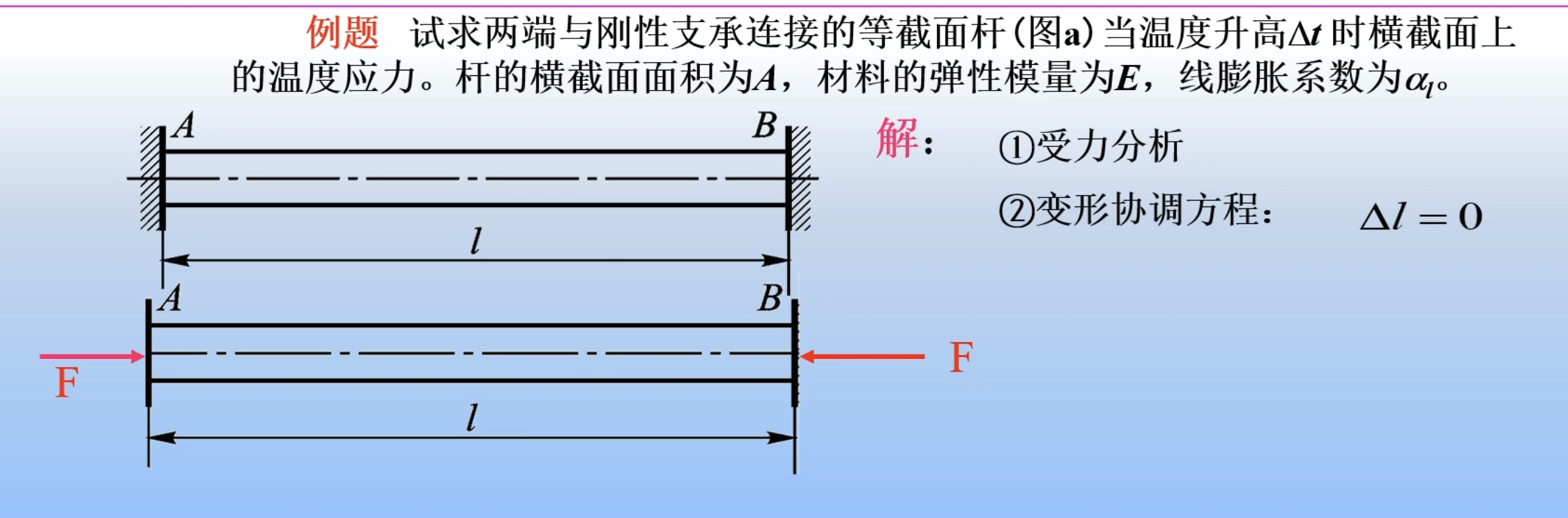
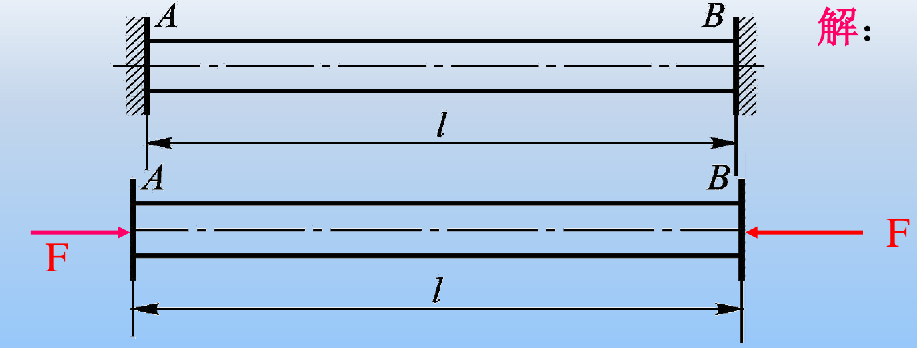
例题:试求两端与刚性支承连接的等截面杆(如图所示)在温度升高 Δt 时横截面上的温度应力。杆的横截面积为 A,材料的弹性模量为 E,线膨胀系数为 αl。
![image-20241222212741306]()
解题步骤:
-
受力分析:由于两端固定,杆无法自由伸长,产生了内力 FN。
-
变形协调方程:根据变形协调关系,杆的总变形量 Δl 为
Δl=ΔlF+ΔlT
由于两端固定,杆总变形量 Δl=0,因此有:
ΔlF+ΔlT=0
其中:
- ΔlF 为力引起的变形,ΔlF=EAFNl
- ΔlT 为温度引起的变形,ΔlT=αlΔt⋅l
- 温度应力计算:将 ΔlF 和 ΔlT 代入变形协调方程:
EAFNl+αlΔt⋅l=0
整理可得内力:
FN=−αlEAΔt
装配应力
由于构件制造尺寸产生的制造误差,在装配时产生变形而引起的应力
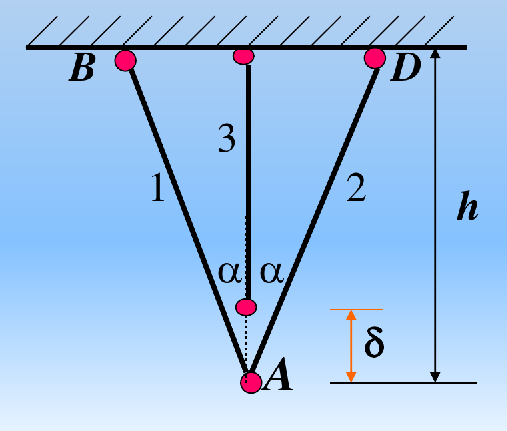
[例题] 如图所示,求杆3因制造误差而短 δ 所引起的装配应力。
![image-20241222213755097]()
[解题步骤]
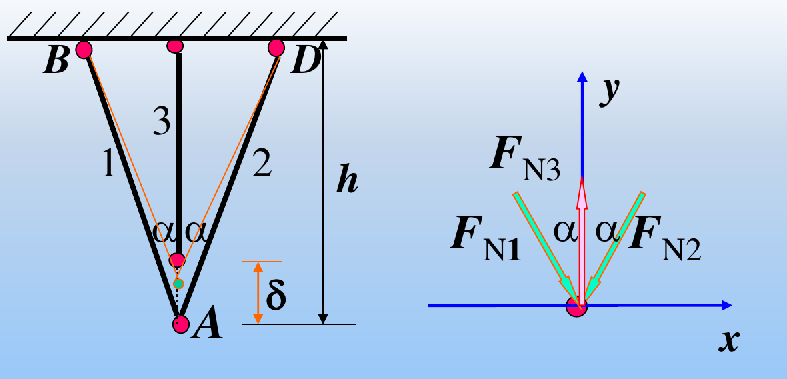
- 绘制受力图
装配后,设杆3受拉力 FN3;杆1、杆2受压力 FN1 和 FN2
根据力的平衡条件,列静力平衡方程:
{FN3−2FN1⋅cosα=0FN1=FN2
得:
FN1=FN2=2cosαFN3(1)
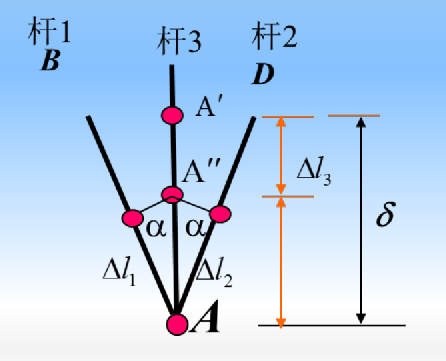
- 变形几何关系
如图所示,节点 A 的新位置为 A′′,节点位移几何关系为:
Δl3=δ−AA′′=δ−cosαΔl1
![image-20241222213831034]()
![image-20241222213847788]()
结合物理方程,代入:
- Δl1=E1A1FN1l1
- Δl3=E3A3FN3l3
得到补充方程:
δ=E3A3FN3l3+cosαE1A1FN1l1(2)
- 综合求解
将 FN1 用 FN3 表示,代入公式(2),整理得:
δ=E3A3FN3l3+cosαE1A12cosαFN3⋅l1
化简得:
FN3=h(1+2cos3α1⋅E1A1E3A3)δE3A3(3)
(3)代入(1)即可得到FN1,FN2
- 应力计算:(代入就好了,这里就不写了)
σ1=A1FN1,σ2=A2FN2,σ3=A3FN3
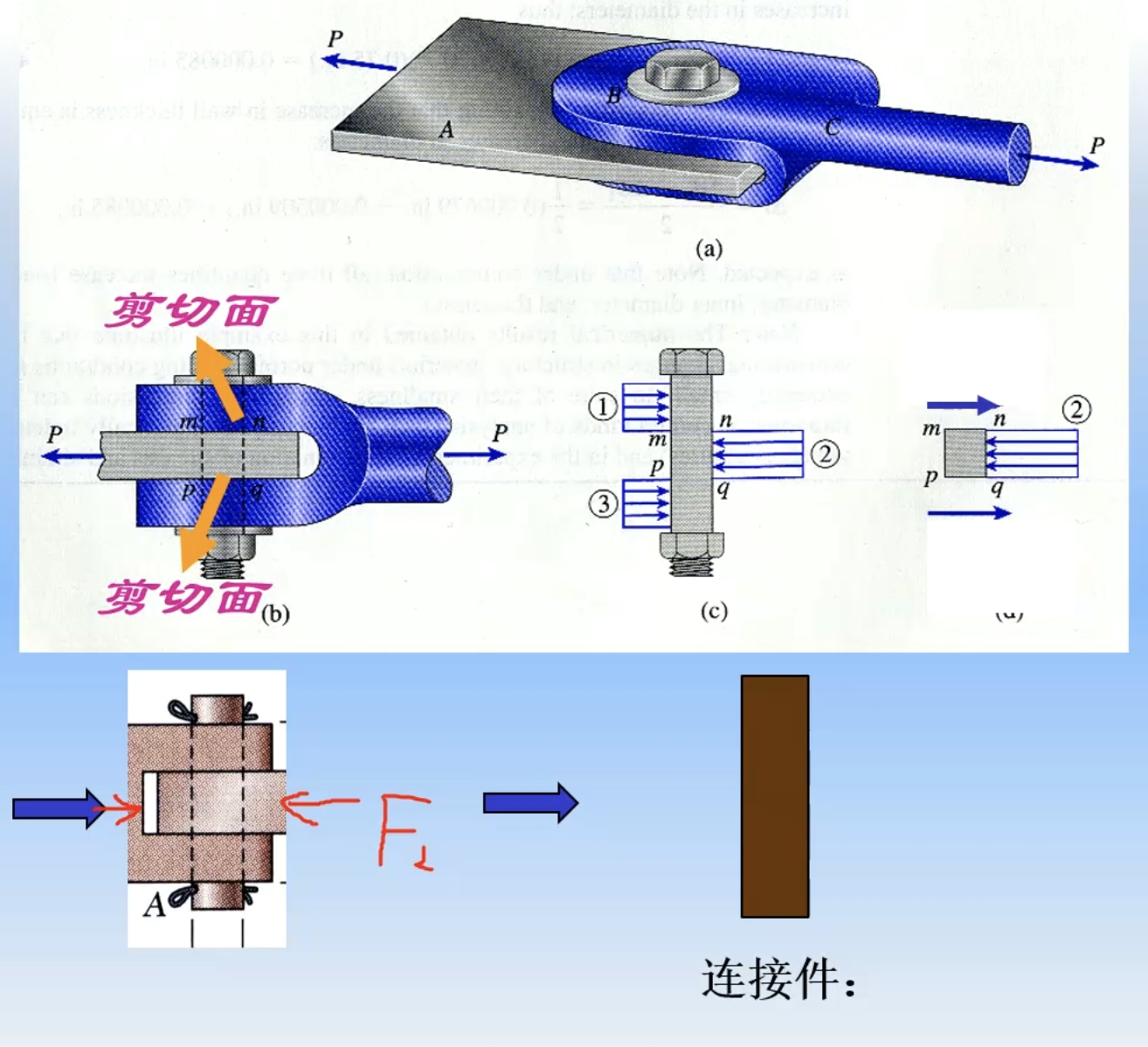
8-9 连接部分的强度计算
连接件分析基本方法
-
对连接件进行受力分析
-
内力:截面法
![]()
两种基本连接件及分析
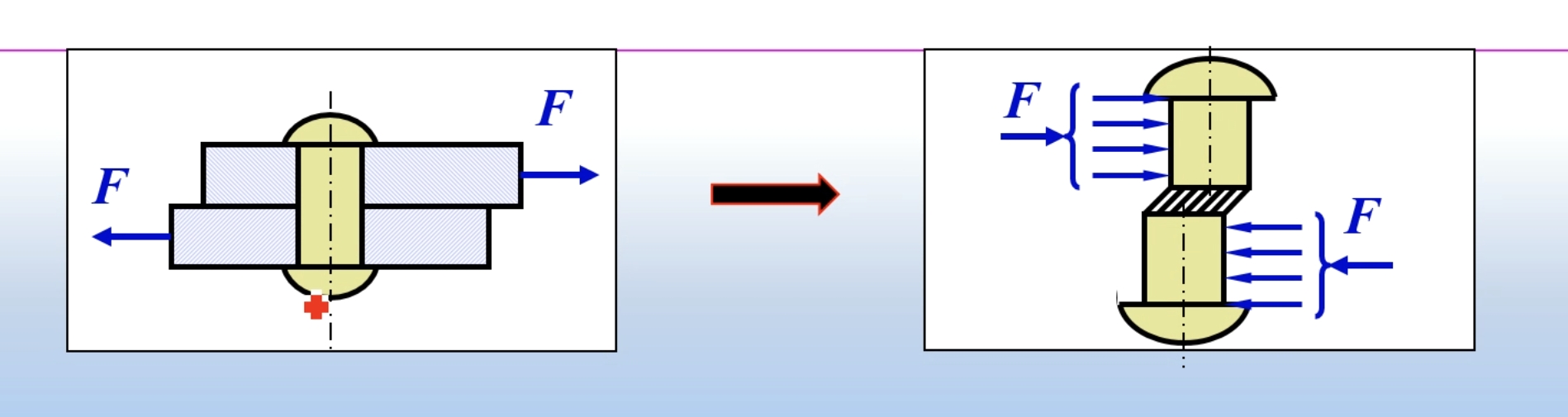
单剪
单剪:有一个剪切面的杆件
![]()
![]()
Fs=F
双剪
![]()
使用截面法分析,两个剪切面上的内力(剪力)均为
Fs=2F
弯矩同样可以直接忽略
剪切概念及其强度计算
实际例子:
连接件是加力点附近的局部应力,非常复杂,所以需要根据实验或模拟结果,假定应力分布规律,再进行计算
剪切强度条件
假设应力均匀分布,实际实验也可以验证这种假设,可以得到剪切强度条件
τ=AFs≤[τ]
类似地,可以解决3类问题:
- 选择截面尺寸
- 确定最大许可载荷
- 强度校核
例题
![]()
挤压概念及其计算
假定挤压应力在有效挤压面上均匀分布
σbs=AbsFb
Abs为有效挤压面(简称挤压面)面积,是指挤压面面积在垂直于总挤压力作用线平面上的投影
挤压强度条件
σbs=AbsFb≤[σbs]
几种接触情况
-
柱面接触:若连接件直径为d,连接板厚度为δ,则柱面接触的有效挤压面面积为δd
- 从这个例子可以直观地看到有效挤压面面积为实际的承压面积在其直径平面上的投影。
Fbs=∫−2π2πσbs2ddθδ⋅cosθ=σbsδd⟹Abs=δd
-
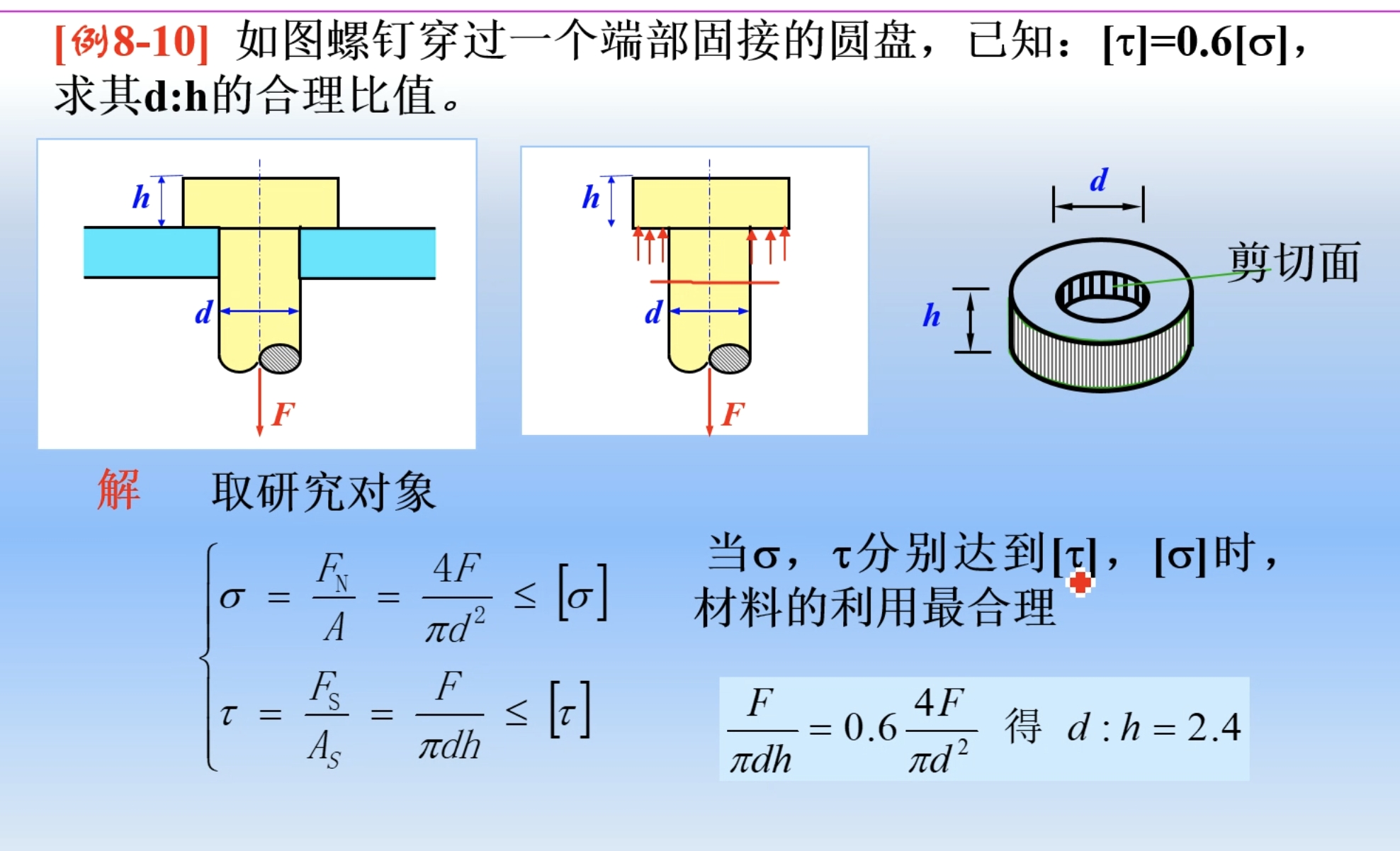
挤压面为平面,有效挤压面就是该面
- 例如下图中螺钉穿过一个端部固接的圆盘,有效挤压面就是圆盘和螺钉直接接触的面
![image-20241223110204545]()
$$
A_{bs} = \frac{\pi}{4}(D^2 - d^2)
$$
综合题目
比如两块或者多块板用铆钉互相固定,然后施加载荷的情况
一般来说这种题目铆钉的位置都是对称性很好的,所以可以先下一个结论,载荷是均匀分布在每个铆钉上的,即如果载荷是P,有n个铆钉,每个铆钉上的力就是nP
- 能出题的肯定是这种情况,要不然我也不知道每个铆钉上的力是怎么分配的,这题目不就没法算了
有了这个结论以后,这种情况就可以按照以下思路全面考虑和处理:
- 考虑铆钉的连接
- 剪切应力
- 挤压应力
- 考虑板的拉伸强度
- 画轴力图
- 找危险截面,需要考虑
- 截面积最小
- 轴力最大
- 计算危险截面上的应力
多块板子的处理方法
- 对称的板子只需要考虑一块就可以了
- 一般两块板子互相拉,算一块就行了
- 两块主板之间搭一块/两块盖板的话,那就要算两块板子:主板+盖板
![image-20241222163946582]()
![image-20241222163836240]()
![]()

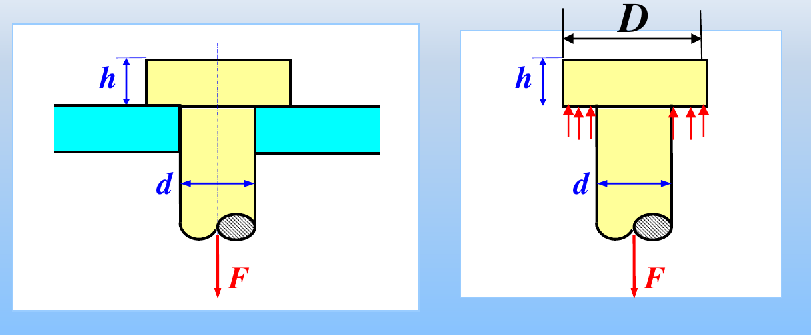 $$
A_{bs} = \frac{\pi}{4}(D^2 - d^2)
$$
$$
A_{bs} = \frac{\pi}{4}(D^2 - d^2)
$$