Chapter9 扭转
9-1 外力偶
可以把扭转的例子抽象为以下计算简图
![]()
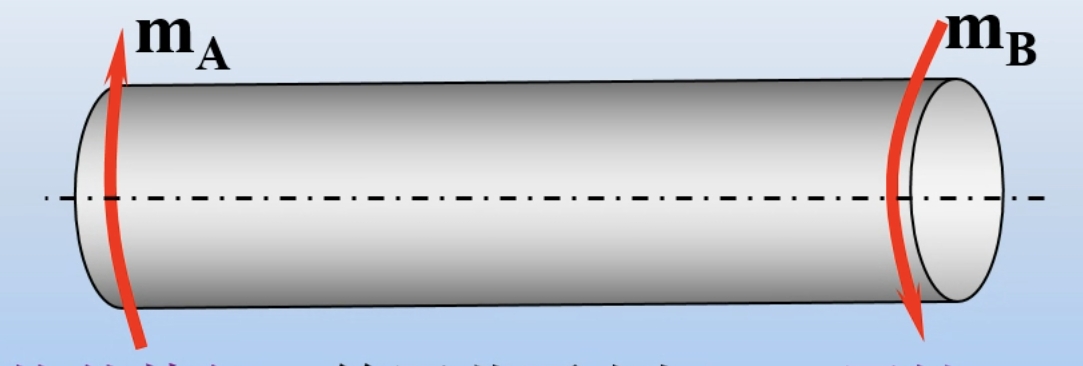
- 构件特征:等圆截面直杆——圆轴
- 受力特征:外力偶矩的作用面与杆件的轴线相垂直
- 变形特征:杆各横截面绕轴线发生相对转动
![]()
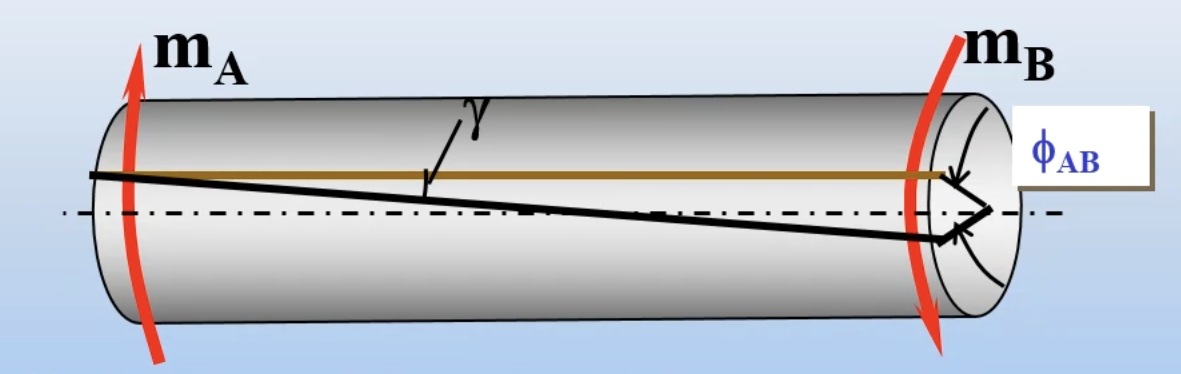
ϕAB为切应变,γ为切应力
作用于轴上的外力偶矩一般不是直接给出的,而是已知轴的转速和传递的功率
此处只研究扭转的情况
外力偶的求法
轴转速n转/分钟,输入输出功率P千瓦,求力偶矩m
P=tW=tms=mω=m602πn⟹m=2π60nP=9.549nP
注意角速度ω的国际单位是rad/s,此处力偶矩m的单位为kN⋅m
对于匀速转动的杆,角加速度α=0,∑Mx=0,即所有外力偶之和为0
9-2 杆件内力偶的分析
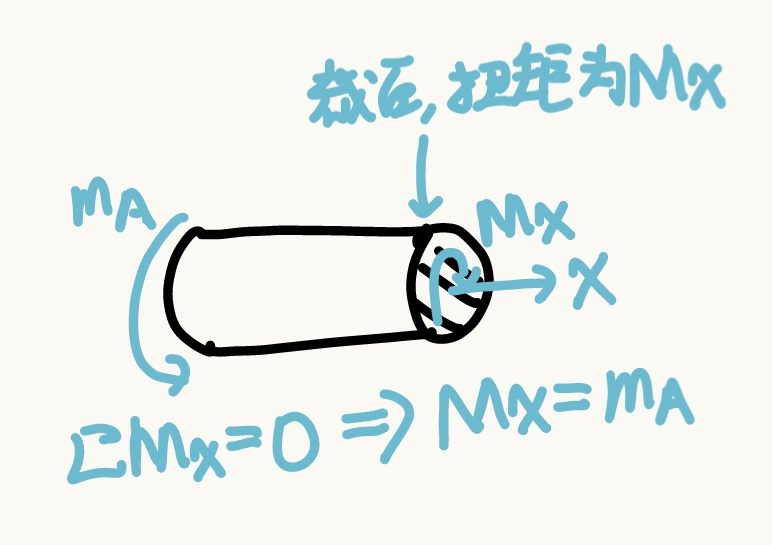
还是使用截面法
![]()
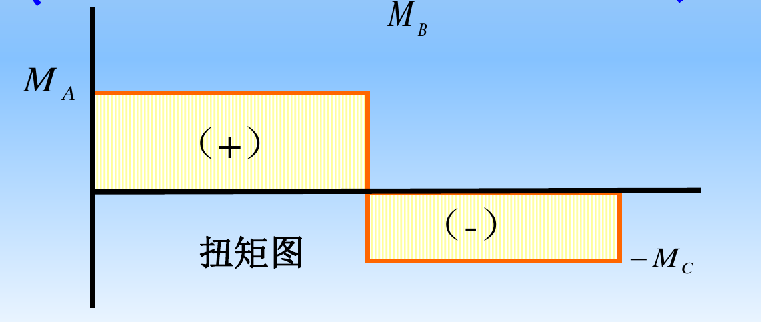
扭矩图:扭矩随构件横截面的位置变化的图线。
![image-20241223141124752]()
方向(符号)的规定:按右手螺旋法则,扭矩矢量的指向与截面外法线的指向一致,为正;反之为负。
![image-20241223140934408]()
9-3 薄壁圆筒的纯扭转应力与两个定理
前提假设
薄壁圆面:沿壁厚应力均匀分布
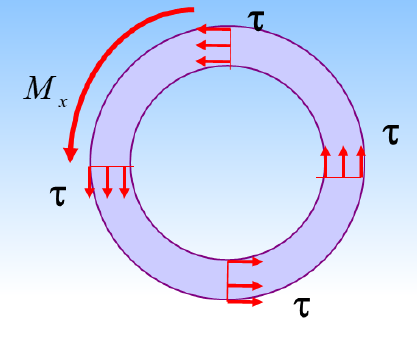
横截面上无正应力,只有切应力,且因为圆周上切应变相同,所以切应力沿圆周均步
切应力方向垂直半径或与圆周相切
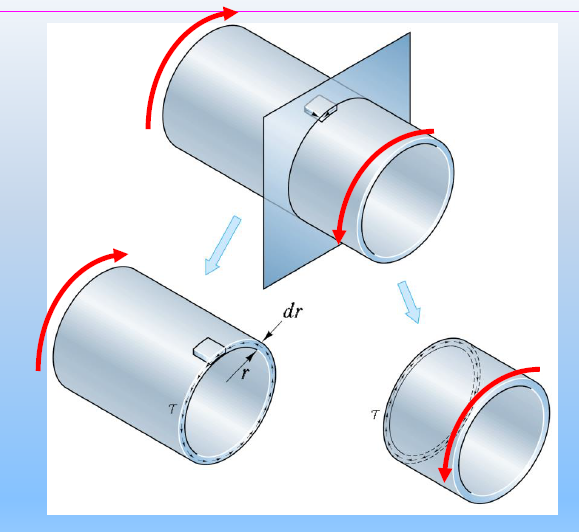
薄壁圆筒的纯扭转应力
设圆筒壁厚为δ,圆筒平均半径为R0,如果δ≤101R0(记住这个近似条件!),则可以认为这是个薄壁圆筒
注意平均半径的含义:如果题目给定内径d,外径D,则平均半径为
R0=2D+d
![image-20241114105018901]()
![image-20241114105115699]()
∫AR0τdA=τR0∫AdA=τR0⋅2πR0δ=Mx⟹τ2πR02δ=Mx⟹τ=2πR02δMx
切应力互等定理
如图,考虑受扭的薄壁圆筒内任一点
![image-20241114105328723]()
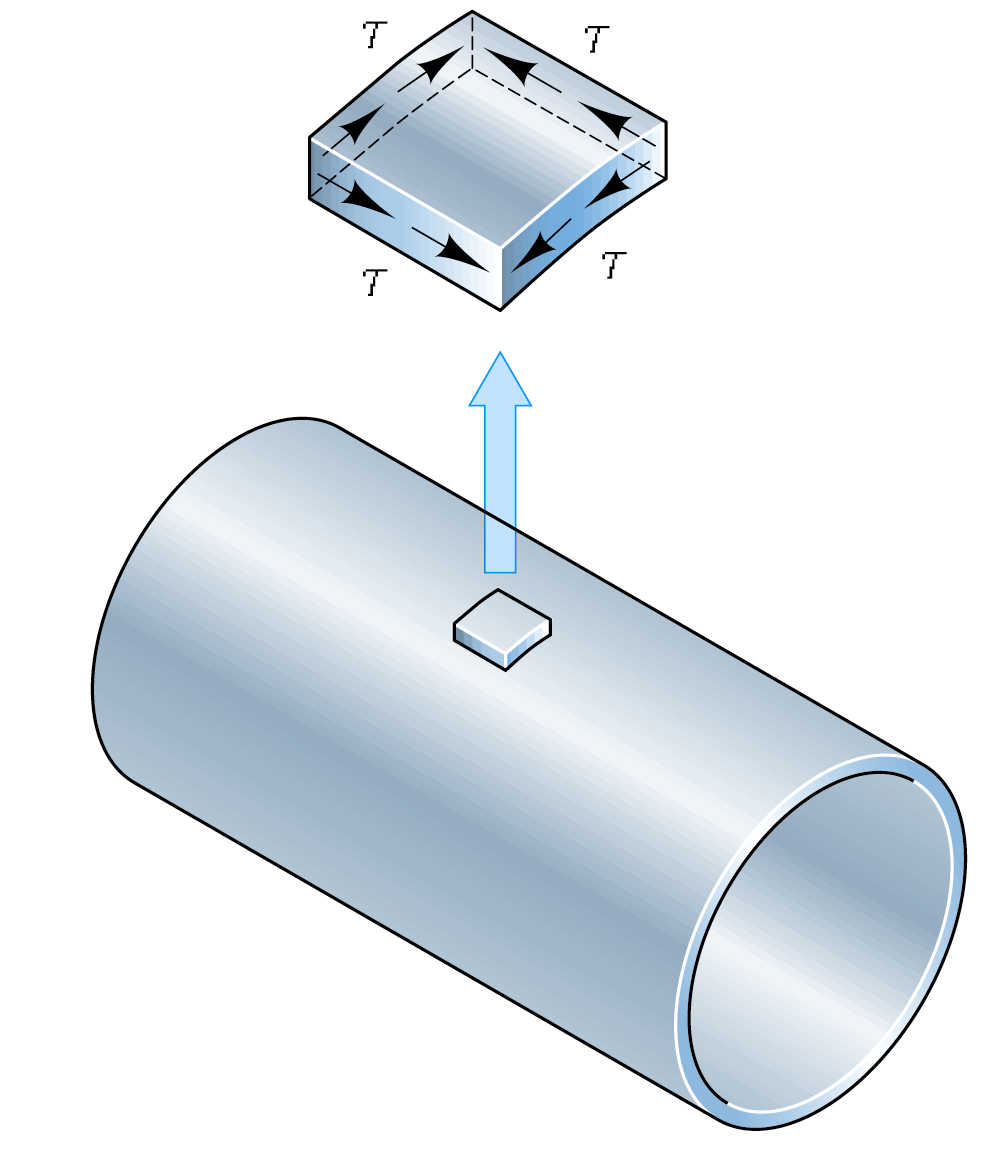
可以取出如下的一块微小的立方体进行分析
![image-20241114105235939]()
(τσdy)dx=(τ′σdx)dy⟹τ=τ′
受力物体内通过任意一点的两个相互垂直截面上的切应力必成对存在,大小相等,方向相反。即切应力同时指向它们的交线或背离它们的交线.
剪切胡克定律
当切应力不超过材料的比例极限τp时,切应力τ与切应变γ成正比
![image-20241114104552498]()
τ=Gγ
其中G是材料的剪切弹性模量
G=2(1+μ)E
9-4 圆轴扭转时的应力和变形
前提假设
刚性平面截面假设:圆轴的横截面变形后保持为平面,相对原来位置转过一个角度
圆轴可以看成许多个套在一起的薄壁圆管,各个薄壁圆管扭转时截面的相对扭转角相同
![image-20241114105735085]()
故横截面上各点切应力的方向:处处垂直于径向,且方向同Mx旋转方向
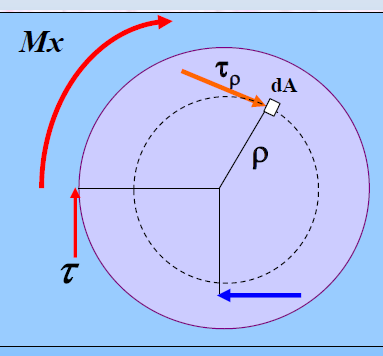
静力平衡条件
由以上假设,可以得到静力平衡条件
Mx=∫Aρτ(ρ)dA
应力和变形分析
形变特性分析
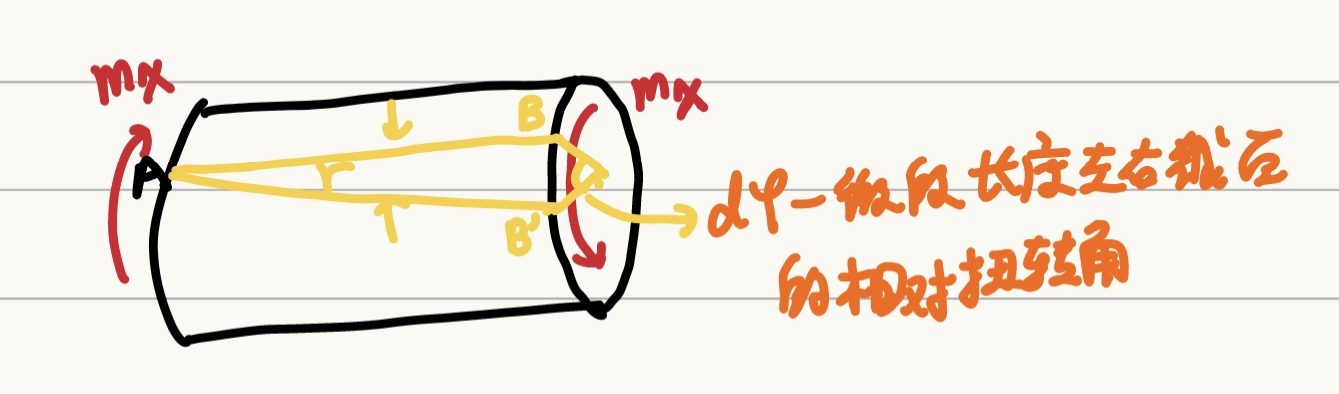
取微段进行分析,即切一个半径为R的微段进行分析,有
![]()
BB′=Rdφtanγ=γ=dxBB′⟹BB′=γdx⟹γdx=Rdφ⟹γ=dxRdφ=Rθ
其中θ是单位长度的扭转角
应力分析
对于一个任意的半径为ρ的微段,就有
γρ=ρdxdφ=ρθ
对于同一截面,θ=const,所以
γρ∝ρ
结合物理条件——剪切胡克定律,可以得到
τρ=Gγρ=Gρθ
与静力平衡条件结合
代入静力平衡条件
Mx=∫ρGρθdA=Gθ∫Aρ2dA=GθIp
其中
Ip=∫Aρ2dA
被称为极惯性矩,是截面的几何性质
θ=GIpMx
其中GIp表示圆轴抵抗变形的能力,称为圆轴的抗扭刚度
τρ=Gρθ=IpMxρ
最大切应力即为
τmax=IPMxR=WpMx
其中Wp=RIp称为抗扭截面模量
常见极惯性矩
实心圆截面
极惯性矩
Ip=∫0Rρ22πρdr=21πR4=321πD4
抗扭截面模量
Wp=RIp=2πR3=16πD3
空心圆截面
Ip=∫rRρ22πρdr=2π(R4−r4)=32π(D4−d4)=32πD4(1−α4)
抗扭截面模量
Wp=RIp=2DIp=16πD3(1−α4)
其中α=Dd
9-5 圆轴的强度条件和刚度条件
强度条件
受扭圆轴破坏的标志
塑性材料:首先发生屈服,最后沿横截面被剪断
脆性材料:变形很小,在与轴线约45度的面上断裂
τmax=WpMx,max≤[τ]
对于恒定截面轴
τmax=WpMx,max
对于变截面轴
τmax=(WpMx)max
讨论:强度相当的情况下,选用哪一种轴更合理?
面积相等的情况下,选用空心轴或实心轴,哪一种强度更高?
变形计算方法
θ=dxdφ=GIpMx⟹dφ=GIpMxdx
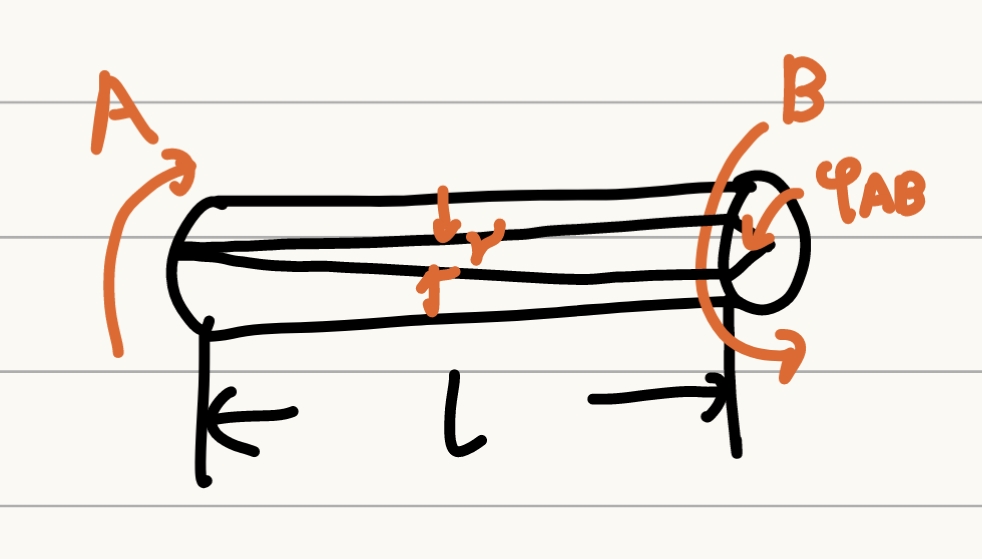
![]()
一般情况下,有
φAB=∫Ldφ=∫LGIpMxdx
φAB为A相对B的扭转角
- 如果在l长度内Mx,G,Ip均相等(恒定情况),那么就有
φ=φAB=GIpMxL
-
阶梯轴或者扭矩不等的阶梯轴(离散的变化情况)
φ=φAB=i=1∑nGiIpiMxili
-
连续变化的情况
φ=∫LG(x)Ip(x)Mx(x)dx
刚度条件
使用单位长度扭转角来进行限制
θmax≤[θ]
或
θmax=GIpMx,maxπ180∘≤[θ](∘/m)
注意:单位一般用度/米
9-6 扭转静不定问题
基本接法
- 静力学关系:建立静力平衡方程
- 变形协调条件:变形协调方程
- 应用扭矩与相对扭转角之间的物理关系(物理方程)φx=GIpMxl,带入变形
- 联立方程,求解
以一个例子来说明
![]()
常见的变形协调条件
- 固定端:固定端之间的角位移为0
- 套管杆结构:杆和套管的角位移应该相等
总结
1
2
3
4
5
6
| graph TD
A[外力] --> B[内力]
B --> C[应力]
B --> D[变形]
C --> E[强度条件]
D --> F[刚度条件]
|