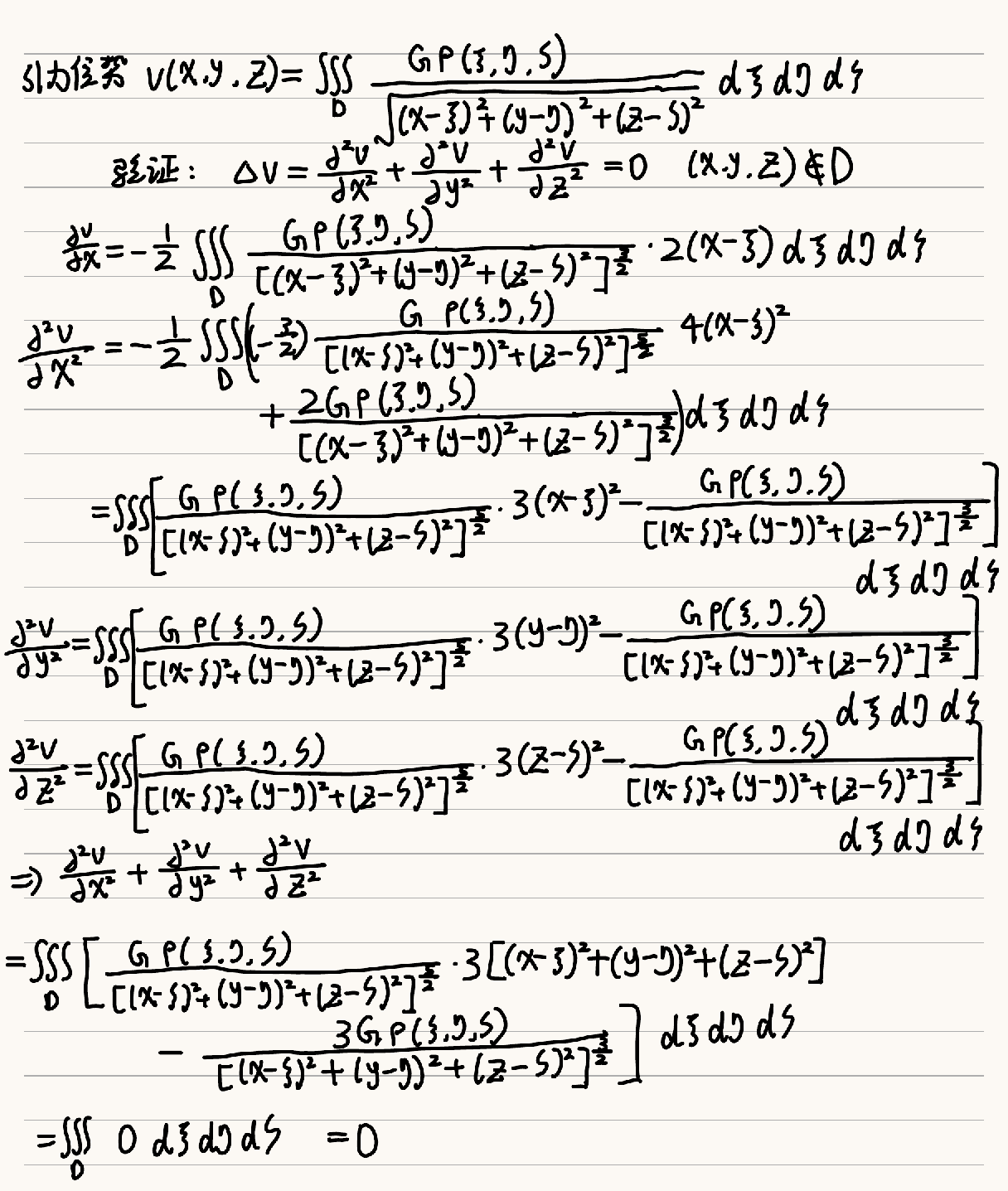数理方法第一章：数理方程

Chapter1 数理方程

问题背景

1.1.1 弦振动方程

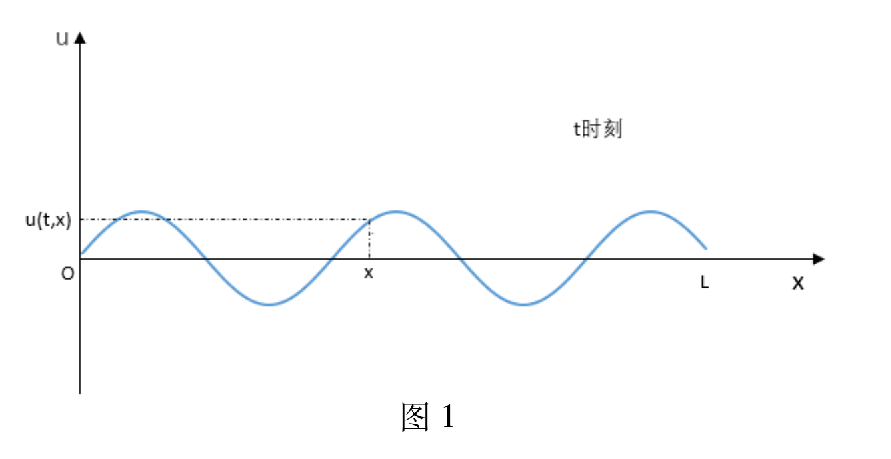
假设一根弦固定在区间$[0,L]$上，假设它的质量密度函数$\rho$是常数，该弦在平衡处附近做微小的横振动

任取该弦上的一个微段$[x,x+\Delta x]$，考察它的运动

该段弧长为

$$\Delta s = \int_{x}^{x+\Delta x} \sqrt{1+\left( \dfrac{\partial u}{\partial x}\right)^2(t,\xi)} \, d\xi$$

由于是微小横振动，故可以进行近似

$$\Delta s \approx \Delta x$$

水平方向上弦没有运动，弦振动方向仅为u-方向

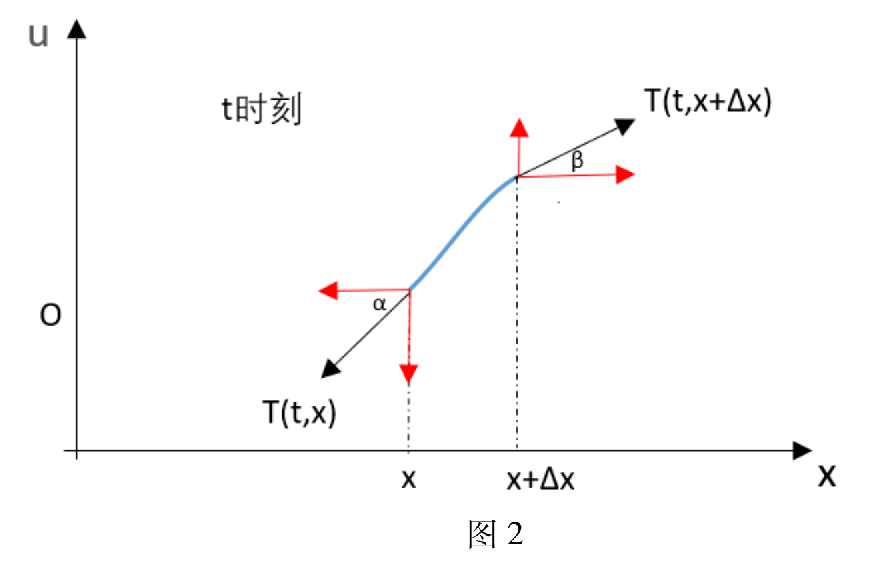
由牛顿第二定律，$F = ma$，结合受力分析，可以列出方程

$$T(x+\Delta x) \cos \beta - T(x) \cos \alpha = 0 \\ \rho \Delta x \dfrac{\partial^2 u}{\partial t^2}(t,\overline{x}) = T(x+\Delta x) \sin \beta - T(x) \sin \alpha + \int_{x}^{x+\Delta x} f(t,\xi) \, d\xi$$

由于假设该弦只是在平衡处做微小的振动，故可以进行如下近似

$$\cos \alpha \approx 1 \quad \cos \beta \approx 1 \\ \sin \alpha \approx \tan \alpha = \dfrac{\partial u}{\partial x}(t,x) \quad \sin \beta \approx \tan \beta = \dfrac{\partial u}{\partial x}(t,x + \Delta x)$$

从而我们有

$$T(x+\Delta x) \approx T(x)$$

由于这个对任意微段$\Delta x$都成立，所以我们可以认为张力在$[0,L]$为常数，记为$T_0$

然后就可以把方程写成

$$\rho \Delta x \dfrac{\partial^2 u}{\partial t^2}(t,\overline{x}) = T_0(\dfrac{\partial u}{\partial x}(t,x + \Delta x) - \dfrac{\partial u}{\partial x}(t,x)) + \int_{x}^{x+\Delta x} f(t,\xi) \, d\xi$$

令$\Delta x \to 0$，就可以得到

$$u_{tt} - a^2 u_{xx} = F(t,x)$$

其中

$$a = \sqrt{\dfrac{T_0}{\rho}} \quad F(t,x) = \dfrac{f(t,x)}{\rho}$$

该方程被成为弦振动方程

1.1.2 热传导方程，扩散方程

前提知识：傅里叶导热定律

三维空间中的形式

$$dQ = -k\dfrac{\partial u}{\partial \vec{n}} dS dt$$

一维线上的形式

$$q = -k u_x$$

推导

考虑$[t_1,t_2]$D中温度从$u(t_1,x,y,z)$变化到$u(t_2,x,y,z)$

所需热量

$$Q_1 = \iiint_{D} \rho c [u(t_2,x,y,z) - u(t_1,x,y,z)] dxdydz$$

热量满足以下关系

$$Q_1 = Q_2 + Q_3$$

$Q_2$为从边界$\partial D$流入的热量，$Q_3$为内部热源提供的热量

由Fourier实验定律，边界处的热量传导满足关系

$$dQ = -k\dfrac{\partial u}{\partial \vec{n}} dS dt$$

其中$k>0$，为热传导系数

从而

$$Q_2 = \int_{t_1}^{t_2} \iint_{\partial D} k \dfrac{\partial u}{\partial \vec{n}} dS dt \\ Q_3 = \int_{t_1}^{t_2} \iiint_{D} f(t,x,y,z) dxdydz dt$$

故可以将热量关系写成

$$\iiint_{D} \rho c [u(t_2,x,y,z) - u(t_1,x,y,z)] dxdydz = \int_{t_1}^{t_2} \iint_{\partial D} k \dfrac{\partial u}{\partial \vec{n}} dS dt + \int_{t_1}^{t_2} \iiint_{D} f(t,x,y,z) dxdydz dt$$

将左边写成对时间积分

$$LHS = \int_{t_1}^{t_2} \iiint_{D} \rho c \dfrac{\partial u}{\partial t} dxdydz dt$$

---

分析：式子右边可以进行如下转化

考虑热流项

$$\dfrac{\partial u}{\partial \vec{n}} = \nabla u \cdot \vec{n}$$

可以把热流项化为

$$\iint_{\partial D} k \dfrac{\partial u}{\partial \vec{n}} dS = \iint_{\partial D} k \nabla u \cdot \vec{n} dS = \iint_{\partial D} k \nabla u d\vec{S}$$

选择热流向量场为

$$\vec{F} = k \nabla u$$

应用高斯定理，可以将热流通量转化为热流向量场的散度的体积分的形式

$$\iint_{\partial D} k \dfrac{\partial u}{\partial \vec{n}} dS = \iiint_{D} \nabla \cdot (k\nabla u) dV = \iiint_{D} k \nabla \cdot (\nabla u) \, dxdydz$$

---

然后整理一下，就可以把右边写成

$$RHS = \int_{t_1}^{t_2} \iiint_{D}(k \nabla \cdot (\nabla u) + f(t,x,y,z)) \,dxdydz \, dt \\ = \int_{t_1}^{t_2} \iiint_{D} \left( k [\dfrac{\partial}{\partial x} \dfrac{\partial u}{\partial x} + \dfrac{\partial}{\partial y} \dfrac{\partial u}{\partial y} + \dfrac{\partial}{\partial z}\dfrac{\partial u}{\partial z}] + f(t,x,y,z) \right) \, dxdydz \, dt$$

进一步可以化简成

$$\rho c \dfrac{\partial u}{\partial t} = k [\dfrac{\partial}{\partial x} \dfrac{\partial u}{\partial x} + \dfrac{\partial}{\partial y} \dfrac{\partial u}{\partial y} + \dfrac{\partial}{\partial z}\dfrac{\partial u}{\partial z}] + f(t,x,y,z)$$

令

$$a^2 = \dfrac{k}{\rho c} \quad \tilde{f} = \dfrac{f}{\rho c}$$

从而可以将热传导方程写成

$$\dfrac{\partial u}{\partial t} - a^2 \Delta u = \tilde{f}$$

一维热传导方程

$$u_t - a^2u_{xx} = f(t,x)$$

推导过程

应用热量守恒定律，进行分析

为了推导热传导方程，我们需要使用热量守恒定律。假设我们考虑长度为 $\Delta x$的杆段 $[x, x + \Delta x]$，则在时间 $t$ 和 $t + \Delta t$ 之间，热量的变化由以下部分组成：

• 热量流入：从左端 $x$ 位置流入的热量为 $q(x, t) \Delta t$。
• 热量流出：从右端 $x + \Delta x$ 位置流出的热量为 $q(x + \Delta x, t) \Delta t$。
• 内部热量变化：由于温度变化，杆段内部的热量变化可以表示为内部能量的变化。假设杆的密度为 $\rho$，比热容为 $c$，则单位体积的热量为 $\rho c u(x, t)$。热量的变化则为：

  $$\text{内部热量变化} = \rho c \frac{\partial u}{\partial t} \Delta x \Delta t$$

根据热量守恒定律，杆段内的热量变化等于流入的热量减去流出的热量：

$$q(x, t) \Delta t - q(x + \Delta x, t) \Delta t = \rho c \frac{\partial u}{\partial t} \Delta x \Delta t$$

空间上的有限差分表示

将右端热流 $q(x + \Delta x, t)$ 用泰勒展开式表示：

$$q(x + \Delta x, t) = q(x, t) + \frac{\partial q}{\partial x} \Delta x + O(\Delta x^2)$$

代入之前的热量守恒方程，并忽略高阶项：

$$q(x, t) \Delta t - \left( q(x, t) + \frac{\partial q}{\partial x} \Delta x \right) \Delta t = \rho c \frac{\partial u}{\partial t} \Delta x \Delta t$$

化简后可以得到：

$$-\frac{\partial q}{\partial x} \Delta x = \rho c \frac{\partial u}{\partial t} \Delta x$$

即：

$$-\frac{\partial q}{\partial x} = \rho c \frac{\partial u}{\partial t}$$

结合傅里叶导热定律

由傅里叶导热定律 $q(x, t) = -k \frac{\partial u}{\partial x}$，将 $q(x, t)$代入上式：

$$-\frac{\partial}{\partial x} \left( -k \frac{\partial u}{\partial x} \right) = \rho c \frac{\partial u}{\partial t}$$

这可以简化为：

$$k \frac{\partial^2 u}{\partial x^2} = \rho c \frac{\partial u}{\partial t}$$

得到结果：一维热传导方程

最后，我们将其整理为标准形式：

$$\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}$$

其中：

$$\alpha = \frac{k}{\rho c}$$

是热扩散系数，单位为 $\text{m}^2/\text{s}$。

初始条件

初始条件即为初始温度分布

$$u(0,x,y,z) = \varphi(x,y,z)$$

边界条件

Robin边界条件

稳定状态热方程和泊松方程的关系

如果$u(t,x)$是下述热方程的解

$$u_t - \Delta u = f(x)$$

其中热源f不依赖于时间t，解$u(t,x)$在$t \to \infty$有极限$\overline{u}(x)$，且此极限状态$\overline{u}$满足下述Poisson方程

$$-\Delta \overline{u} = f(x)$$

1.1.3 调和方程，Poisson方程

引力场

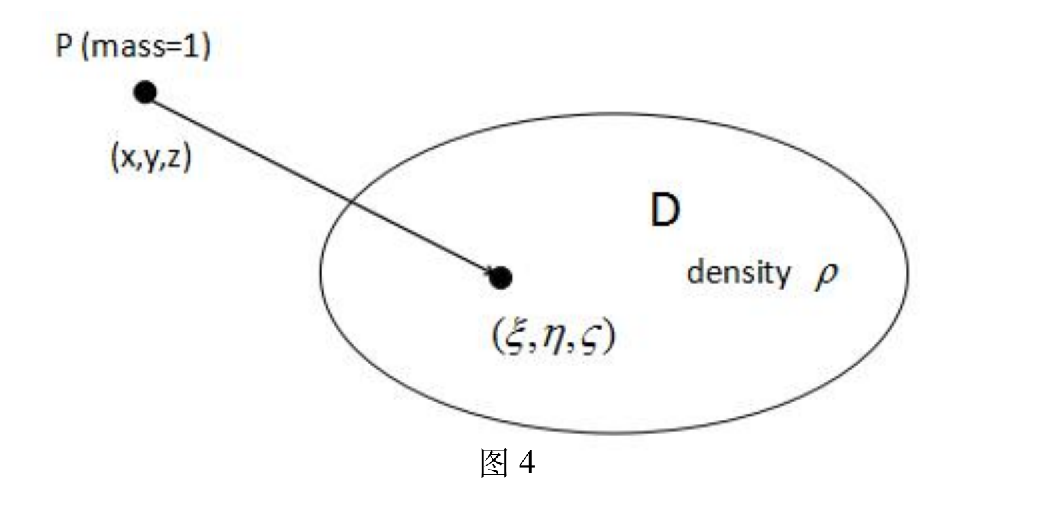
1. 考虑D为空间中质量为M的质点的情况

   在空间$R^3$中给定一个物体D，其质量密度是$\rho(x,y,z)$，考虑空间中引力位势所满足的方程

   由万有引力定律，

   $$\vec{F} = \dfrac{G M}{r^2} \dfrac{\vec{PD}}{r}$$

   其中距离为

   $$\vec{PD} = (x-x_0,y-y_0,z-z_0) \\ r = \lvert PD \rvert = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2}$$

   可以写成

   $$F = -\dfrac{GM}{r^2} (\dfrac{x-x_0}{r},\dfrac{y-y_0}{r},\dfrac{z-z_0}{r})$$

   考虑位势函数

   $$\varphi(x,y,z) = \dfrac{GM}{r} = \dfrac{GM}{\sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2}}$$

   可以得到

   $$\nabla \varphi = \vec{F}$$

2. 一般情况

考虑引力微元

$$d\vec{F} = -\dfrac{G\rho(\xi,\eta,\zeta)}{r^2} (\dfrac{x-x_0}{r},\dfrac{y-y_0}{r},\dfrac{z-z_0}{r}) d \xi d \eta d \zeta$$

总引力为

$$\vec{F} = - \iiint_D \dfrac{G\rho(\xi,\eta,\zeta)}{r^2} (\dfrac{x-x_0}{r},\dfrac{y-y_0}{r},\dfrac{z-z_0}{r}) d \xi d \eta d \zeta$$

其中

$$r = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2}$$

引力位势为

$$v(x,y,z) = \iiint_D \dfrac{G\rho(\xi,\eta,\zeta)}{r} d \xi d \eta d \zeta \\ = \iiint_D \dfrac{G\rho(\xi,\eta,\zeta)}{\sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2}} d \xi d \eta d \zeta$$

可以验证

$$\Delta v = 0$$

其中Laplace算子为

$$\Delta \phi = \nabla^2 \phi = \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} + \frac{\partial^2 \phi}{\partial z^2}$$

这就是Laplace方程

电场（电势函数）

1. 应用高斯定理

首先，利用 高斯通量定理（Gauss’ flux theorem）来描述电场 $\mathbf{E}$ 和电荷分布之间的关系。图中提到的高斯定理是：

$$\int_{\Gamma} \mathbf{E} \cdot \mathbf{n} \, dS = \frac{1}{\epsilon_0} Q$$

其中：

• $\Gamma$ 是包围电荷的闭合曲面的边界。
• $\mathbf{n}$ 是指向外的单位法向量。
• $\epsilon_0$ 是真空介电常数。
• $Q = \int_D \rho \, dV$ 是区域 $D$ 内的总电荷量，$\rho$ 是电荷密度。

根据高斯定理，电场通量与总电荷成正比。

2. 将高斯定理转化为体积分形式

通过 散度定理（数学上的高斯定理），将曲面积分转化为体积分：

$$\int_{\Gamma} \mathbf{E} \cdot \mathbf{n} \, dS = \int_D \nabla \cdot \mathbf{E} \, dV$$

因此，结合高斯定理，我们可以得到：

$$\int_D \nabla \cdot \mathbf{E} \, dV = \frac{1}{\epsilon_0} \int_D \rho \, dV$$

由于该等式对任意区域 $D$ 都成立，因此积分号可以去掉，得到点形式：

$$\nabla \cdot \mathbf{E} = \frac{1}{\epsilon_0} \rho$$

这就是麦克斯韦方程组中的 高斯定律，它表明电场的散度等于电荷密度 $\rho$ 除以介电常数 $\epsilon_0$。

3. 结合库仑定律

根据 库仑定律，电场 $\mathbf{E}$ 可以通过电势函数 $\varphi$ 表示为：

$$\mathbf{E} = -\nabla \varphi$$

将这个表达式代入高斯定律$\nabla \cdot E = \frac{\rho}{\epsilon_0}$中，得到：

$$\nabla \cdot (-\nabla \varphi) = \frac{1}{\epsilon_0} \rho$$

化简后，得到拉普拉斯算子的形式：

$$-\nabla^2 \varphi = \frac{1}{\epsilon_0} \rho$$

因此，电势函数 $\varphi$ 满足的方程为：

$$\nabla^2 \varphi = -\frac{1}{\epsilon_0} \rho$$

这就是 Poisson 方程，用于描述电势函数 $\varphi$ 在电荷分布 $\rho$ 影响下的空间分布。

4. Poisson 方程的形式

总结得到的 Poisson 方程 为：

$$\Delta \varphi = -\frac{1}{\epsilon_0} \rho$$

其中 $\Delta$ 是拉普拉斯算子，表示为：

$$\Delta \varphi = \nabla^2 \varphi = \frac{\partial^2 \varphi}{\partial x^2} + \frac{\partial^2 \varphi}{\partial y^2} + \frac{\partial^2 \varphi}{\partial z^2}$$

最终表达式

$$\boxed{\Delta \varphi = -\frac{1}{\epsilon_0} \rho}$$

这就是 Poisson 方程，用于描述在三维空间中电荷分布 $\rho$ 产生的电势函数 $\varphi$。

具体的计算验证过程如下：

1.2 基本概念与叠加原理

1. 线性的PDE的解满足线性叠加原理，也就是说一个线性PDE的两个解线性叠加以后得到的仍然是这个线性PDE的解
2. 初边值问题有方程齐次边界条件非齐次，方程非齐次边界条件齐次等情况
3. 适定性=存在性+唯一性+稳定性
   • 稳定性指的是定解问题的解连续依赖于源项$f$，初始数据$(\phi,\psi)$和边界数据$(\mu_1.\mu_2)$，也就是如果其中一部分有轻微扰动，对解的影响也是轻微的

线性叠加原理