Chapter7 Sampling

Chapter7 采样理论

采样的基本概念

采样 (Sampling)：是将连续时间信号 $x(t)$ 转换为离散时间序列的过程。在实际应用中，模拟信号处理功能有限且成本高昂，因此数字信号处理应用广泛。而采样是数字信号处理的前提，通过模数转换器（ADC）实现。

冲激串采样 (Impulse-Train Sampling)

这是理想化的采样模型。原始信号 $x(t)$ 与一个由狄拉克 $\delta$ 函数组成的冲激串 $p(t)$ 相乘，得到采样信号 $x_p(t)$ 。

采样函数 (Sampling Function)： $p(t) = \sum_{n=-\infty}^{\infty}\delta(t-nT)$ ，其中 $T$ 是采样周期。
采样信号 (Sampled Signal)：

$x_p(t) = x(t)p(t) = \sum_{n=-\infty}^{\infty}x(nT)\delta(t-nT)$

$x(nT)$ 称为原始信号的样本 (Samples)。

采样周期 (Sampling Period)： $T$ 。
采样频率/采样率 (Sampling Frequency/Sampling Rate)： $\omega_s = 2\pi/T$ (角频率) 或 $f_s = 1/T$ (频率)。

2. 采样面临的问题

采样过程有什么要求？
- 采样率要求：奈奎斯特定律
如何从采样信号中恢复原始信号？

二、采样信号的频谱

理解采样信号的频谱是判断能否恢复原始信号的关键。
由于 $x_p(t) = x(t)p(t)$ ，根据傅里叶变换的乘积定理（时域相乘对应频域卷积），采样信号的频谱 $X_p(j\omega)$ 为：

$X_p(j\omega) = \frac{1}{2\pi} [X(j\omega) * P(j\omega)]$
其中：
- $X(j\omega)$ 是原始信号 $x(t)$ 的频谱。
- $P(j\omega)$ 是采样函数 $p(t)$ 的频谱，它本身也是一个冲激串：
  
  $P(j\omega) = \mathcal{F} [p(t)] = \frac{2\pi}{T} \sum_{n=-\infty}^{\infty}\delta(\omega - n\omega_s)$
将 $P(j\omega)$ 代入，得到采样信号的频谱：

$X_p(j\omega) = \frac{1}{T} \sum_{n=-\infty}^{\infty} X(j(\omega - n\omega_s))$

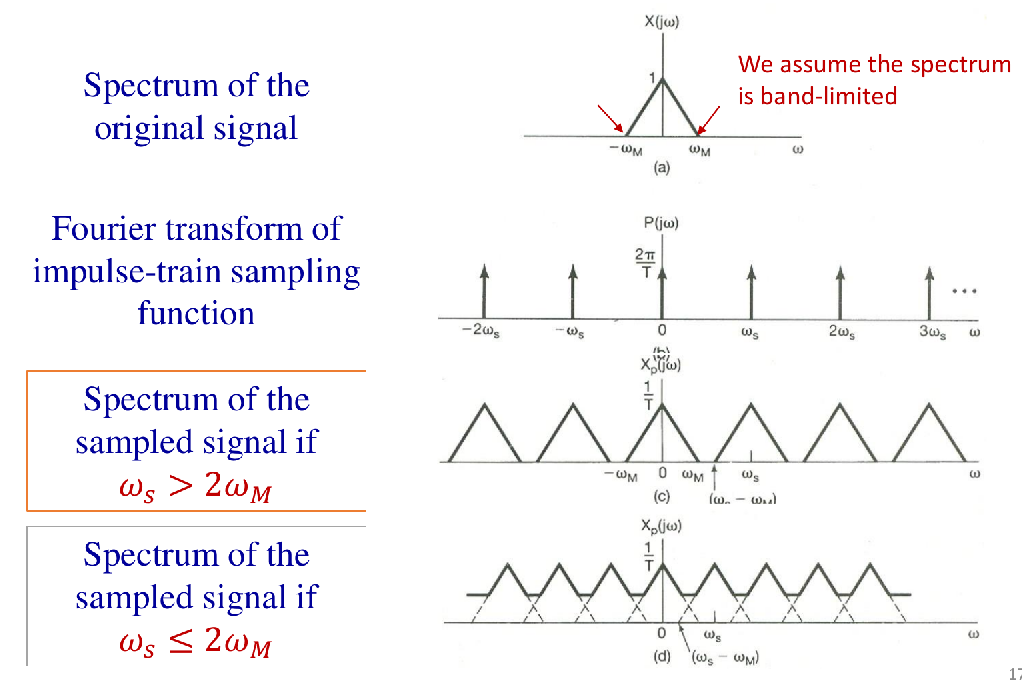
结论：采样信号的频谱是原始信号频谱以采样频率 $\omega_s$ 为周期进行周期性延拓，并乘以因子 $1/T$ 得到的。

三、奈奎斯特-香农采样定理 (Nyquist-Shannon Sampling Theorem)

该定理给出了从采样信号无失真恢复原始信号的条件。

1. 频谱不混叠的条件
假设原始信号 $x(t)$ 是带限信号，即其频谱 $X(j\omega) = 0$ 对于 $|\omega| > \omega_M$ ，其中 $\omega_M$ 是原始信号的最高角频率。

无失真恢复的条件：当采样频率 $\omega_s > 2\omega_M$ 时，采样信号频谱中各个周期延拓的频谱不会发生重叠。
频谱混叠 (Aliasing)：当采样频率 $\omega_s \le 2\omega_M$ 时，采样信号频谱中各个周期延拓的频谱会发生重叠，导致原始频谱失真，无法完美恢复原始信号。

2. 信号的重建 (Reconstruction)
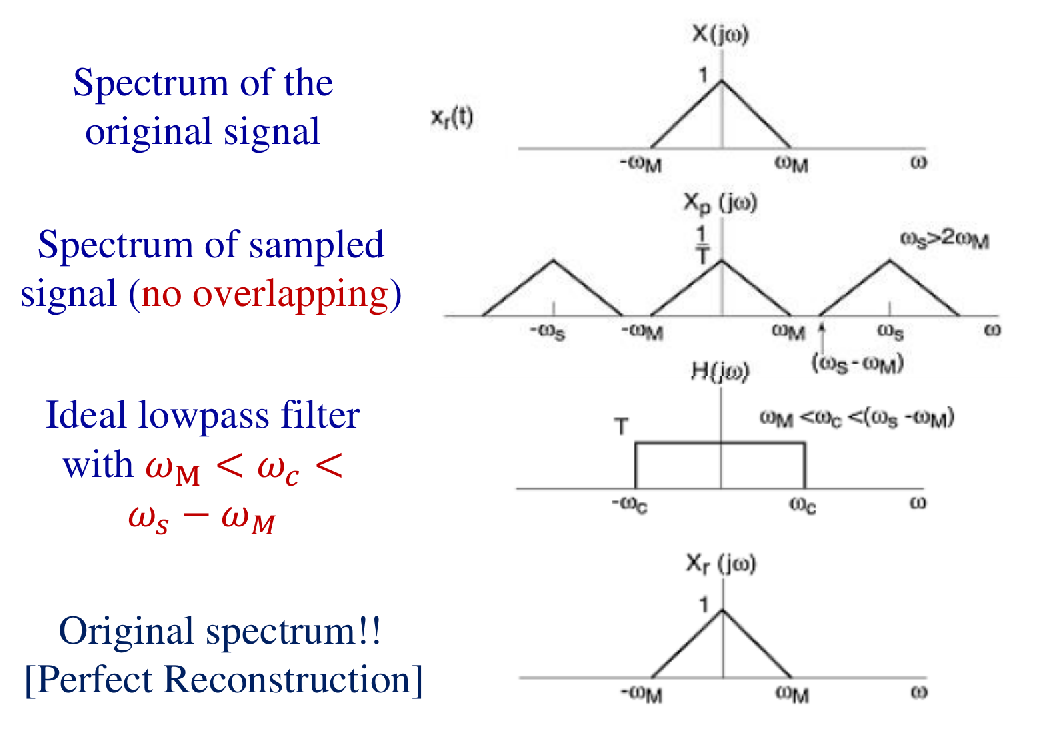
当满足 $\omega_s > 2\omega_M$ 时，可以通过一个理想低通滤波器从采样信号 $x_p(t)$ 中恢复原始信号 $x(t)$ 。

理想低通滤波器特性：
- 增益： $T$
- 截止频率 $\omega_c$ ：满足 $\omega_M < \omega_c < \omega_s - \omega_M$

3. 采样定理的陈述

一个带限于 $\omega_M$ （即 $X(j\omega)=0$ 对于 $|\omega|>\omega_M$ ）的连续时间信号 $x(t)$ ，如果其采样频率 $\omega_s > 2\omega_M$ ，那么 $x(t)$ 可以由其样本序列 $\{x(nT)\}$ 唯一确定。重建过程如下：

生成冲激串采样信号： $x_p(t) \stackrel{\Delta}{=} \sum_{n=-\infty}^{\infty} x(nT)\delta(t-nT) = \sum_{n=-\infty}^{\infty}x(nT)\delta(t-nT)$ 。
将 $x_p(t)$ 通过一个增益为 $T$ ，截止频率满足 $\omega_M < \omega_c < \omega_s - \omega_M$ 的理想低通滤波器。滤波器的输出即为原始信号 $x(t)$ 。

4. 重要术语

奈奎斯特频率 (Nyquist Frequency)：信号的最高频率 $\omega_M$ (或 $f_M$ ) 。
奈奎斯特率 (Nyquist Rate)：能够无失真恢复信号的最低采样频率 $2\omega_M$ (或 $2f_M$ )。实际采样频率必须高于奈奎斯特率。

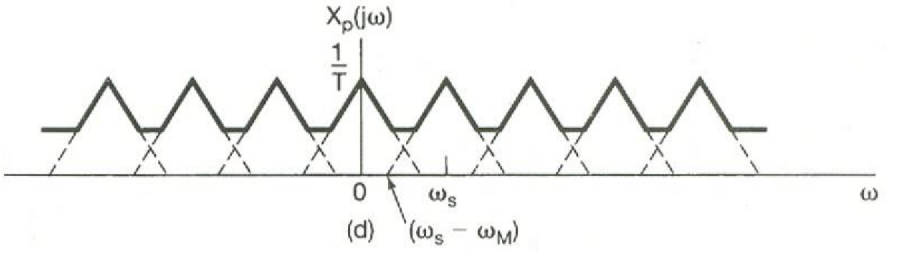
四、频谱混叠 (Aliasing)

当采样频率不满足 $\omega_s > 2\omega_M$ 时，就会发生频谱混叠。

现象：在重建信号时，原始信号中高于 $\omega_s/2$ 的频率成分会“混叠”到低于 $\omega_s/2$ 的频带内，表现为低频成分。
影响：导致重建信号失真，无法代表原始信号。例如，一个高频的正弦信号在发生混叠后，可能被重建为一个低频的正弦信号。
- **以正弦信号为例：**考虑原始信号为 $x(t) = \cos(\omega_0 t)$ $x (t) = cos (ω_{0} t)$ ，采样频率为 $\omega_s$ $ω_{s}$ 。
  - 无混叠 ( $\omega_0 < \omega_s/2$ )：重建信号 $x_r(t) = \cos(\omega_0 t)$ ，与原始信号相同。
  - 发生混叠 ( $\omega_0 > \omega_s/2$ )：如果使用截止频率为 $\omega_c = \omega_s/2$ $ω_{c} = ω_{s} /2$ 的理想低通滤波器进行重建，高频信号 $\cos(\omega_0 t)$ $cos (ω_{0} t)$ 会被重建为低频信号 $\cos((\omega_s - \omega_0)t)$ $cos ((ω_{s} - ω_{0}) t)$ （或其他与 $\omega_0$ $ω_{0}$ 和 $\omega_s$ $ω_{s}$ 的整数倍相关的频率，具体取决于 $\omega_0$ $ω_{0}$ 落在哪个混叠区域）。
    - 例如，如果原始信号频率 $\omega_0 = \frac{4\omega_s}{6}$ （此时 $\omega_0 > \omega_s/2$ ），重建后的信号频率将是 $\omega_s - \omega_0 = \omega_s - \frac{4\omega_s}{6} = \frac{2\omega_s}{6}$ 。一个较高频率的信号在采样和重建后表现为一个较低频率的信号。
    - 同样，如果 $\omega_0 = \frac{5\omega_s}{6}$ ，重建后信号频率为 $\omega_s - \omega_0 = \frac{1\omega_s}{6}$ 。
发生原因：采样频率相对于信号的最高频率来说过低。

五、模数转换器 (ADC) 与实际采样方法

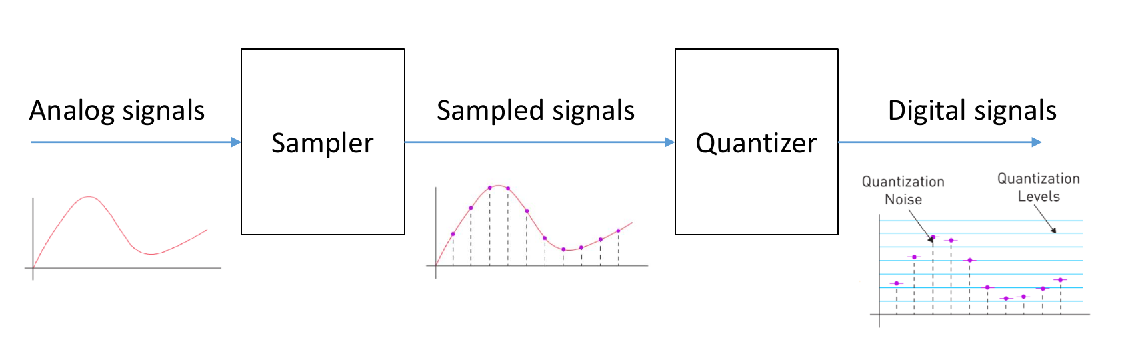
1. ADC 的组成

ADC 通常由采样器 (Sampler) 和量化器 (Quantizer) 组成。
量化过程会引入量化噪声。

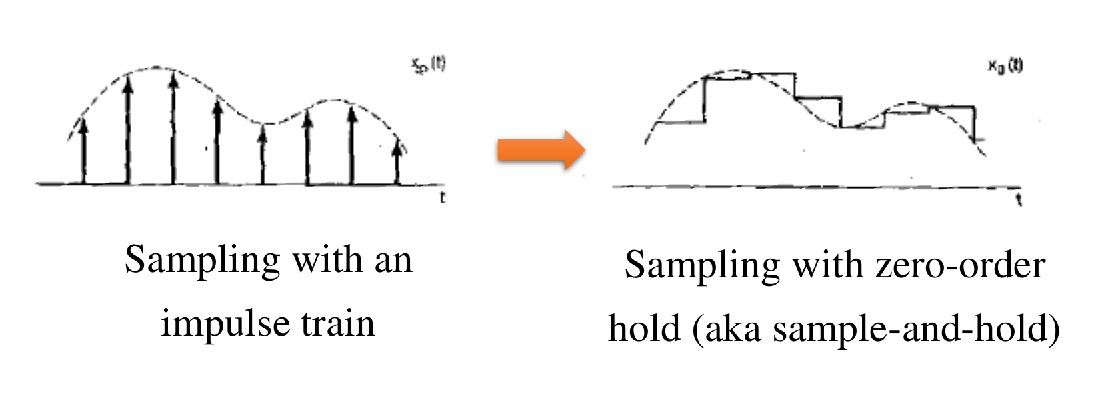
2. 零阶保持采样 (Zero-Order Hold, ZOH)
冲激串采样在物理/电路上难以实现。零阶保持采样是一种更实际的采样方法。

过程：采样得到的样本值在下一个采样点到来之前保持不变，形成阶梯状的信号 $x_0(t)$ 。
数学表示：可以看作冲激串采样信号 $x_p(t)$ $x_{p} (t)$ 与一个宽度为 $T$ $T$ 、高度为 1 的矩形脉冲 $h_0(t)$ $h_{0} (t)$ (从0到T) 进行卷积。
$x_0(t) = x_p(t) * h_0(t)$
- 其中 $h_0(t) = \begin{cases} 1, & 0 \le t < T \\ 0, & \text{otherwise} \end{cases}$

3. ZOH 采样信号的频谱

$X_0(j\omega) = X_p(j\omega)H_0(j\omega)$

其中

$X_p(j\omega) = \frac{1}{T}\sum_{n=-\infty}^{\infty}X(j(\omega-n\omega_s))$
$H_0(j\omega)$ 是矩形脉冲 $h_0(t)$ 的傅里叶变换：

$H_0(j\omega) = \frac{\sin(\omega T/2)}{\omega/2} e^{-j\omega T/2} = T \text{sinc}(\frac{\omega T}{2\pi}) e^{-j\omega T/2}$

若sinc定义为 $\frac{\sin(\pi t)}{(\pi t)}$
公式：
$H_0(j\omega) = \frac{2\sin(\omega T/2)}{\omega}e^{-j\frac{\omega T}{2}}$

影响： $H_0(j\omega)$ 是一个Sinc函数形状的频谱（幅度上），它会对 $X_p(j\omega)$ 的各个复制频谱产生衰减，尤其是在高频部分。

4. ZOH 采样的重建

条件：仍然需要满足 $\omega_s > 2\omega_M$ 。
重建滤波器：由于 $H_0(j\omega)$ 对频谱的“塑形”作用，重建时不能直接使用理想低通滤波器，而是需要在理想低通滤波器的基础上加上一个补偿滤波器（或称为“逆滤波器”）来抵消 $H_0(j\omega)$ 的影响。
理想的重建滤波器 $H_r(j\omega)$ 应该满足：

$H_0(j\omega)H_r(j\omega) = H_{ideal\_LPF}(j\omega) = \begin{cases} T, & |\omega| < \omega_c \\ 0, & |\omega| > \omega_c \end{cases}$
- 通常取 $\omega_c = \omega_s/2 = \pi/T$

$H_r(j\omega) = \frac{H_{ideal\_LPF}(j\omega)}{H_0(j\omega)} = \frac{H_{ideal\_LPF}(j\omega) \cdot \omega e^{j\frac{\omega T}{2}}}{2\sin(\omega T/2)}$

这个重建滤波器的频率响应在幅度上是理想低通滤波器的基础上，对 $H_0(j\omega)$ 的倒数进行补偿，相位上则补偿 $H_0(j\omega)$ 引入的线性相位。

六、抗混叠滤波器 (Anti-Aliasing Filter)

为了防止频谱混叠，在 ADC 进行采样之前，通常会使用一个抗混叠滤波器。

类型：这是一个模拟低通滤波器。
作用：滤除原始模拟信号中高于奈奎斯特频率 ( $\omega_s/2$ ) 的频率成分，确保输入到采样器的信号是真正带限的，从而避免混叠。
设计考虑：需要仔细设计以保证陡峭的过渡带和良好的响应速度。

七、数模转换器 (DAC) 与内插 (Interpolation)

DAC 的核心是内插，即根据离散的样本点生成连续的模拟信号。
内插公式：给定样本序列 $f(nT)$ ，内插信号 $\hat{f}(t)$ 表示为：

$\hat{f}(t) = \left(\sum_{n=-\infty}^{\infty}f(nT)\delta(t-nT)\right) * h(t) = \sum_{n=-\infty}^{\infty}f(nT)h(t-nT)$

其中 $h(t)$ 是内插基函数 (Interpolation Basis)。

主要内插方法：

1. Sinc 内插 (理想内插 / 带限内插)

基函数： $h(t)$ 是一个 Sinc 函数，其频谱对应一个理想低通滤波器。
$h(t) = \text{sinc}(\frac{t\omega_c}{\pi})$ (若截止频率为 $\omega_c$ )
特性：如果其频率响应的截止频率为 $\omega_s/2$ ，则可以实现完美重建。
优点：理论上可以完美恢复信号，不需要额外的重建滤波器。
缺点：Sinc 函数在时域上是无限长的，物理上不可实现，因此仅具有理论意义。

2. 零阶保持内插 (Zero-Order Interpolation)

基函数： $h_0(t)$ ，一个从 0 到 $T$ 的矩形脉冲。
特性：在每个采样点之间保持前一个采样值不变，形成阶梯状信号（分段常数逼近）。
优点：实现简单（与ZOH采样电路类似）。
缺点：内插后的信号不连续，通常需要在其后接一个重建滤波器以平滑信号。

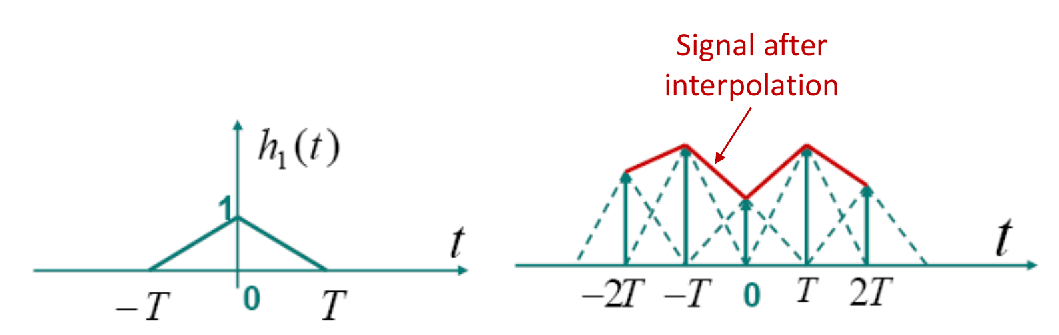
3. 一阶保持内插 (First-Order Interpolation / 线性内插)

基函数： $h_1(t)$ ，一个从 $-T$ 到 $T$ 的三角形脉冲（顶点在 $t=0$ 处，值为1）。
特性：用直线连接相邻的采样点，形成分段线性逼近。
优点：实现相对容易，生成的信号比零阶保持更平滑。如果不追求完美重建，有时可以省略重建滤波器。
缺点：信号的导数不连续（在采样点处）。

实际应用中，如果内插方法能产生足够平滑的信号，有时为了节省成本，可以不使用复杂的模拟重建滤波器。